F1 Score, Confusion Matrix, Precision & Recall (trade-off) 왕초보를 위한 설명

여러 대회의 평가 metric으로 사용되는 F1 Score와 이를 이해하는데 필요한 여러 개념들을 정리한 글입니다.

부족한 것이 많아 잘못 이해하고 작성한 것이 있을 수 있으니 너그러이 이해해주시고 피드백 해주신다면 너무 감사하겠습니다. 🙇‍♂️

(가장 중요한 내용들은 글의 최하단에 간단히 요약해두었으니 정리가 필요하신 분들은 마지막만 보셔도 좋습니다!!)

 

F1 Score

F1 Score는 어떤 실험이나 예측이 제대로 이루어졌는지 확인할 수 있는 지표입니다.
precision과 recall의 조화 평균(harmonic mean)으로 구합니다.

이 수식을 이해하기 위해선 Confusion Matrix(혼동 행렬), 그리고 여기에 포함되는 precision(정밀도), recall(재현율)의 개념을 알아야 합니다.

 

본 게시물에서는 조화 평균에 대해서 자세히 설명하지 않을 것입니다.

따라서 산술/기하/조화 평균에 대한 이해가 필요하신 분은 아래 블로그 포스팅을 통해 공부하시는 것을 추천드립니다.

(친구가 작성한 글인데 정리가 너무 잘 되어있습니다 👍🏻)

https://ssunbell.github.io/posts/Math-%EC%82%B0%EC%88%A0%ED%8F%89%EA%B7%A0,-%EA%B8%B0%ED%95%98%ED%8F%89%EA%B7%A0,-%EC%A1%B0%ED%99%94%ED%8F%89%EA%B7%A0%EC%9D%98-%EC%9D%98%EB%AF%B8/

[Math]산술평균, 기하평균, 조화평균의 의미

 

Confusion Matrix(혼동 행렬)

혼동 행렬은 이진 분류, 즉 두 가지 항목으로 구분하는 것에 대한 행렬입니다.

간단히 어떤 것을 긍정 혹은 부정으로 구분하는 작업에 대한 평가를 내리고 있다고 이해하면 쉽습니다.

출처 : https://towardsdatascience.com

먼저 이 행렬을 이루고 있는 글자들이 무엇을 의미하는지 살펴보겠습니다.

 

두 개의 알파벳으로 이뤄진 TP, FP, FN, TN, 이 녀석들은 각각 "참/거짓 + 긍정/부정"을 나타내고 있습니다.

순서대로 해석한 것은 다음과 같습니다.

• True Positive : 진짜 긍정, 실험결과를 통해 긍정이라고 판단한 것이 실제로 긍정인 경우
• False Positive : 가짜 긍정, 실혐결과를 통해 긍정이라고 판단했지만 실제로는 부정인 경우
• False Negative : 가짜 부정, 실험 결과를 통해 부정이라고 판단했지만 실제로는 긍정인 경우
• True Negative : 진짜 부정, 실험 결과를 통해 부정이라고 판단한 것이 실제로 긍정인 경우

이렇게만 보면 이 내용들이 무엇을 의미하는지 이해하기 어렵습니다.

따라서 구체적인 예시를 확인해봅시다.

100명의 사람들을 대상으로 감기에 걸렸는지 확인하는 테스트를 진행합니다.
100명 중 실제로 감기에 걸린 사람은 총 20명입니다.
하지만 테스트 결과 감기에 걸린 사람은 15명인 것으로 밝혀졌습니다.
또한 감기에 걸렸다고 확인된 15명 중, 10명은 실제로 감기에 걸린 사람들이지만 나머지 5명은 감기에 걸리지 않은 사람들입니다.

밑줄 친 내용들을 보며 위의 혼동 행렬이 어떻게 구성되는지 생각해봅니다.
감기에 걸린 것을 positive(양성), 그렇지 않은 것을 negative(음성)라고 가정하죠.

• True Positive
  • 위 테스트에서 감기에 걸린 사람은 15명이라고 했습니다. 그 중에서도 실제로 감기에 걸린 사람들은 10명입니다.
    이 사람들은 실제로도 positive이고 테스트 결과도 positive인 것입니다.
• False Positive
  • 그렇다면 나머지 다섯 명은 '양성이라고 잘못 판단된' 케이스겠죠.
    이 사람들은 실제로 감기에 걸리지 않았지만, 즉 실제로는 negative이지만 positive로 판단된 다섯 명이 여기에 해당됩니다.
• Fasle Negative
  • 감기에 걸리지 않았다고 테스트를 통과했지만 실제로는 그렇지 않은 경우입니다.
    즉, 실험 결과는 negative인데 실제로는 postive라는 뜻이죠.
    100명 중 실제로 감기에 걸린 사람은 20명인데 제대로 걸러진 것은 10명밖에 되지 않는다는 것을 확인했습니다.
    따라서 감기에 걸린 20명 중 negative로 판별되었을 10명이 여기에 해당됩니다.
• True Negative
  • 실제로 감기에 걸리지도 않았고 테스트 결과도 감기에 걸리지 않은 것으로 나온 사람들입니다.
    원래 감기에 걸리지 않았던 사람들은 80명이었습니다.(총 100명 중 20명이 감기에 걸렸으니까요)
    하지만 이들 중 5명은 감기에 걸린 것으로 잘못 판단 되었음을 위에서 확인했습니다(False Positive).
    따라서 원래 negative이면서 테스트 결과도 negative인 75명이 여기에 해당됩니다.

이제 위 내용을 바탕으로 confusion matrix를 다시 그려 볼까요?

TP	FP	실제 현황
FN	TN	감기에 걸림	감기에 걸리지 않음	합계
테스트 결과	감기에 걸림	10(TP)	5(FP)	15
	감기에 걸리지 않음	10(FN)	75(TN)	85
합계		20	80	100

 

 

Precision & Recall

Precision = True Positive / Actual Results, Recall = True Positive / Predicted Results
(Precision = TP / (TP + FP), Recall = TP / (TP + FN))

한글로는 아주 간단한 하게도 정밀도와 재현율입니다.

식으로 이해하는 것은 쉽지 않습니다.

혼동 행렬을 이쁘게 구성해두었으니 이를 활용해서 이해해보죠.

 

• Precision(정밀도)

우리는 감기에 걸렸다고 판단된 사람들 중 진짜 감기에 걸린 사람들이 누구인지 정확히 알고 싶습니다.

따라서 양성(positive), 즉 감기에 걸렸다고 판단된 사람들 중에서, 실제로 감기에 걸린 사람들의 비율을 확인하는 것입니다.
감기에 걸렸다고 판단된 사람들 중에는 실제 감기에 걸리지 않았던 사람도 있다는 점을 잊으면 안 됩니다!

 

이를 혼동 행렬의 정보를 통해 표현하면 다음과 같습니다.

정밀도(precision)

= 테스트 결과가 양성이면서 실제로 양성인 사람 / 테스트 결과가 양성으로 나온 사람

= TP / (TP + FP) = 10 / (10 + 5) = 2/3 = 66.7%

 

여기서 우리가 주목해야 할 것은 FP(False Positive)입니다.

감기에 걸렸다고 판단되었지만 실제로는 감기에 걸리지 않은 사람들이죠.

정밀도를 높이기 위해서는 이 사람들의 숫자(FP)를 줄이는 것이 테스트의 목표가 될 것입니다.

 

결국 '실제로는 음성이지만 테스트를 통해 양성이라고 판단되는 비율을 줄이는 것'을 의미하고,

그 비율이 많이 낮을수록 정밀도는 1에 가까운 값이 될 것입니다.

 

• Recall(재현율)

또다른 관점에서, 우리는 실제 감기에 걸린 사람들 중 얼마나 많은 사람들이 테스트를 통해 감기에 걸렸다고 판단되었는지를 알아보고 싶습니다.

이것 또한 테스트가 얼마나 유의미했는지 판단할 수 있는 지표가 되겠죠.

재현율(recall)

= 테스트 결과가 양성이면서 실제로 양성인 사람 / 실제로 양성인 사람

= TP / (TP + FN) = 10 / (10 + 10) = 1/2 = 50%

 

마찬가지로 우리는 FN(False Negative)에 주목할겁니다.

이는 감기에 걸리지 않았다고 판단되었지만 실제로는 감기에 걸린 사람들이죠.

이런 사람의 숫자를 줄이는 것은 분명 재현율이라는 지표의 값을 높이는데 도움이 될 것입니다.

이것도 마찬가지로 FN이 줄어든다면 1에 가까운 수치가 될 것입니다.

 

•  Trade-off Precision & Recall, threshold

그럼 이렇게 한 번 생각해볼까요?

실제로는 양성이지만 테스트를 통해 음성으로 판단된 사람들(FN)이 있습니다.

이 숫자를 줄인다는 것이 무엇을 의미할까요?

 

바로 실제로 양성이면서 테스트를 통해서도 양성으로 판단되게 만든다는 것입니다.

말만 들으면 FN에 속하는 사람들을 TP로 옮긴다는 것 같습니다.

(이제는 FN과 TP가 무엇을 의미하는지 다시 떠올리면서 이해해보세요 😄)

❌ 하지만 이처럼 단순히 볼 수 있는 문제가 아닙니다!! ❌

 

먼저 우리가 시도한 테스트에 대해 다시 정의해보겠습니다.

100명의 사람들에 대해 각 사람이 감기에 걸렸는지를 확인하는 테스트
테스트 결과 어떤 사람이 감기에 걸렸을 확률이 50% 이상이라면 양성, 그렇지 않다면 음성 판정을 내린다.

이를 그래프로 표현하면 다음과 같습니다.

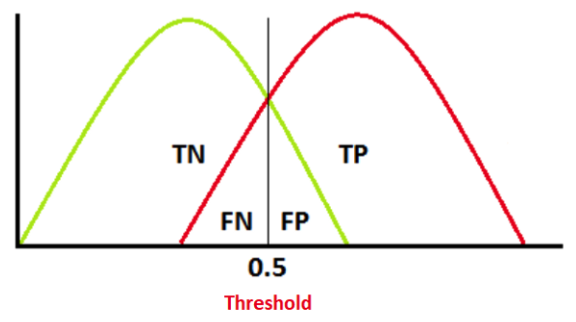
• 당황하지 마세요..! Threshold(임계점)는 방금 테스트 정의에 나타난 "확률"입니다!
• 초록색 그래프는 negative인 사람들을 아우르고 있고, 빨간색 그래프는 positive인 사람들을 아우르고 있습니다.
  즉, 통계적으로는 두 특징의 사람들이 엄격히 구분되지 않고 섞여있다고 해석할 수 있습니다.
  또한 threshold를 기준으로 좌측은 negative 판정을 내리고, 우측은 positive 판정을 내린다는 것을 알 수 있습니다.
  (x축이 threshold, 감기에 걸렸을 확률을 의미하게 됩니다)
• 따라서 우리가 정한 확률을 기준으로 negative/positive가 구분되며, 실제 제대로 판단을 내린 것들은 TN/TP가 되고 판단을 잘못 내린 것은 FN/FP가 됩니다.

 

하나만 더 생각해볼까요? 🙃

저기 중간의 임계점을 오른쪽으로, 그러니까 0.7정도로 옮기면 어떻게 될까요?

다시 말하자면 '감기에 걸렸을 확률이 70% 이상일 때만 positive로 판정'한다는 의미입니다.

• FN의 범위는 커지고 FP의 범위는 줄어들게 됩니다.
• 어..? FN은 Recall(재현율)과, FP는 Precision(정밀도)와 연관이 있지 않았나요?
  기억이 안나실까봐 정의를 다시 보여드리면 이와 같습니다.
  Precision = TP / (TP + FP), Recall = TP / (TP + FN)
• 따라서 임계점을 높인다는 것은 '보다 엄격하게 테스트를 진행 하겠다'는 뜻이 됩니다.
  FP의 값은 줄어들었으므로 precision의 값은 커집니다(FP가 분모에 있으므로).
  반대로 FN의 값은 커졌으므로 recall의 값은 작아집니다(FN이 분모에 있으므로).
• 바로 이어서 반대 상황을 생각해보면 '보다 여유있게 테스트를 진행 하겠다'고 했을 땐(임계점을 낮추었을 때),
  precision의 값은 줄어들고 recall의 값은 커질 것입니다.

 

하지만 이런 의문을 가질 수도 있습니다.

🙋🏼 만약 두 특징의 사람들이 완벽히 구분된다면 어떻게 되나요? 

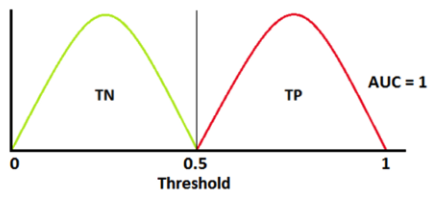
이런 경우라도 임계점을 좌우로 움직이다 보면 FN/FP가 발생할 것입니다.
하지만 recall이 줄어든다고 해서 precision이 늘어나거나 하는 trade-off 관계가 정확히 성립하지 않을 것입니다.

 

그렇다면 이런 형태의 분포가 과연 "현실세계"에 존재할 수 있을까요?
예상하신 것처럼 존재할 수 없습니다 😅

애초에 이런 분포의 형태도 "확률"에 의해 계산된 것이니까요!

 

위에서 중요한 것들을 많이 다루었으니 직관적으로만 이해하고 넘어가보겠습니다.

우리는 100명의 사람들에 대해 80명은 negative, 20명은 positive라고 정해주었습니다.
🤔 이건 100% 사실일까요?

역시 사실이 아니겠죠..! 😂

 

고등학교에서 배웠던 "구간 추정"의 개념이 기억나실지 모르겠네요.

대충 95%, 99% 정확도로 추정하기 위해 어떤 값들을 곱하고 하던 정도만 기억해내시면 됩니다!

(정확도를 높이기 위해 추정 구간의 길이를 늘리던 내용이었습니다)

 

무슨 말이냐면 우리가 정한 80/20명의 구분은 사실이 아니라 "추정의 결과"라는 것입니다.

몇 퍼센트의 정확도로 추정했는지는 정하지 않았음에도 불구하고 우리는 100%라고 가정을 해버린 것이죠!

추정에서 100%는 존재할 수 없기 때문에 실제로는 precision과 recall이 항상 trade-off 관계를 이루고 있다,
라고 당당히 말할 수 있습니다 ㅎㅎ

(이진 분류의 성능을 측정하는 지표로 AUC, ROC를 이용할 수 있는데 이는 다음 포스팅에서 다뤄볼 예정입니다)

 

 

 

마지막으로 이 내용들을 기반으로 해서 F1 Score가 무엇인지 정리하고 마무리하겠습니다.

F1 Score

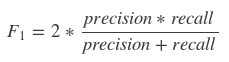
이제는 precision과 recall의 의미를 이해하셨으리라 믿습니다!

두 지표는 하나가 높아지면 나머지 하나가 줄어드는 관계에 있습니다.

또한 둘 중 하나가 무조건 더 중요한 것도 아니죠.

 

그래서 우리는 둘 사이의 평균을 구할 것이고, 이때 조화 평균을 이용합니다.

(앞서 말씀드린 것처럼 조화 평균이 무엇인지 기억나지 않는 분들은 위에 올려둔 블로그를 방문해보세요 😀)

 

macro & weighted & micro

정말 마지막입니다!

우리가 떠올렸던 테스트는 "이진 분류"였다는 것을 기억하고 계시나요?

감기에 걸렸다 or 감기에 걸리지 않았다 처럼 둘 중 하나로 구분하는 테스트였습니다.

하지만 이 외에도 엄청나게 많은 종류로 구분할 수 있을 것입니다.

 

이를테면 어떤 동물을 보고 강아지, 고양이, 호랑이, 사슴, 토끼 등등으로 구분하라고 할 수도 있겠죠.

이런 종류들을 class라고 부릅니다.

class가 여러 개 있을 때 f1 score를 구하는 방식은 크게 세 가지로 나뉩니다.

왼쪽부터 차례로 macro, weighted, micro F1 Score

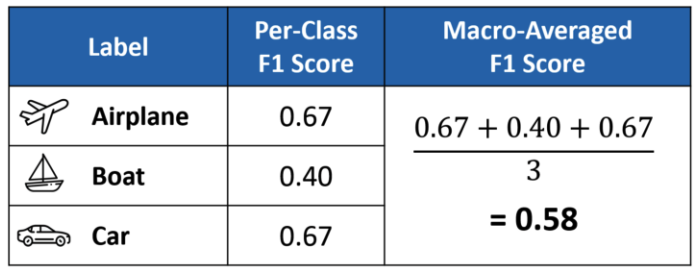
1) macro : class가 여러 개 있을 때 단순 평균값을 구하는 방식은 macro 입니다.

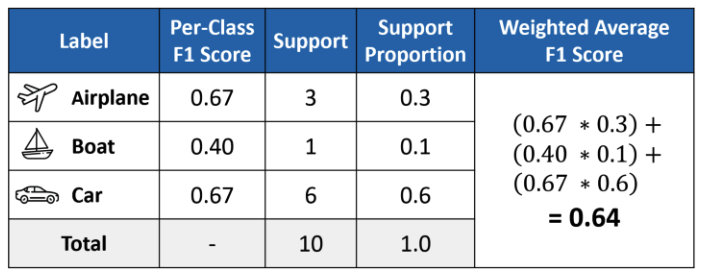
2) weighted : 하지만 각 class에 포함되는 자료의 개수가 다르다면 가중치를 부여하는 방식을 떠올릴 수도 있습니다.

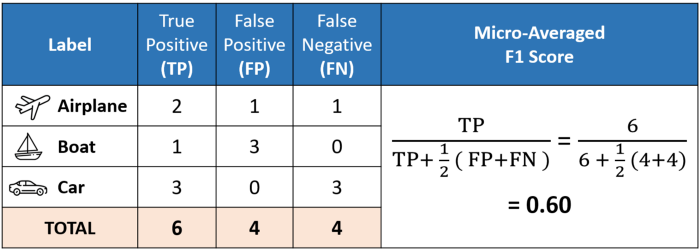
3) micro : 마지막으로 애초에 f1 score를 구할 때부터 자료의 개수를 합치는 방식도 존재합니다.

 

특히 micro f1 score의 경우 class의 분포가 불균형(imbalanced)할 때 적절한 평가 방식이 될 수 있다는 것도 직관적으로 이해할 수 있습니다. 😋

 

이상으로 F1 score에 대해서 자세히 알아보았습니다! 👏🏻👏🏻👏🏻

 

F1 Score 총정리

1. F1 Score는 precision(정밀도)과 recall(재현율)의 조화 평균으로 구한다.
2. precision과 recall은 confusion matrix(혼동 행렬)를 통해 이해할 수 있다.
    어떤 것에 관심이 있는지에 따라서 중요도가 달라질 수 있다.
    ex) 암에 걸린 환자를 찾고 싶은 업무의 경우 '암에 걸리지 않은 환자를 암으로 진단하는 것'보다 '암에 걸린 환자를 놓치는 것'이 더 심각한 문제일 것이다. 이때는 'recall'이 'precision'보다 더 중요한 평가지표로 쓰일 수 있다.
3. precision과 recall은 threshold(임계점)에 따라 서로의 비율을 빼앗는 trade-off 관계에 있다.
    현실 세계에서는 반드시 trade-off 관계라고 볼 수 있다.
    ( = 둘 다 동시에 올리는 것은 불가능하다, 한 쪽을 높이면 반대쪽을 포기해야 한다.)
    + 일반적으로 threshold가 올라가면 precision이 상승하고 recall이 줄어든다.(반대도 마찬가지)
4. F1 Score는 class의 종류에 따라 macro, weighted, micro 방식으로 구분하여 적용할 수 있다.
    이때 imbalanced한 class 분포에 대해서는 micro 방식이 적절하다.

 

Reference

https://towardsdatascience.com/micro-macro-weighted-averages-of-f1-score-clearly-explained-b603420b292f

Micro, Macro & Weighted Averages of F1 Score, Clearly Explained

https://junklee.tistory.com/116

매크로 평균(Macro-average) vs 마이크로 평균(Micro-average)

https://medium.com/@chenzhivis/precision-recall-tradeoff-2e3903d54a89

Precision recall tradeoff

https://towardsdatascience.com/

Towards Data Science

https://youtu.be/n9lQudF9J5g