목차
1. Simple neural networks

- neural network를 이루는 작은 원 하나를 neuron이라고 한다.
- 그 구조는 활성화 함수인 시그모이드에 가중치 w와 입력 a를 곱하고 b를 더한 값을 집어넣는 것이다.
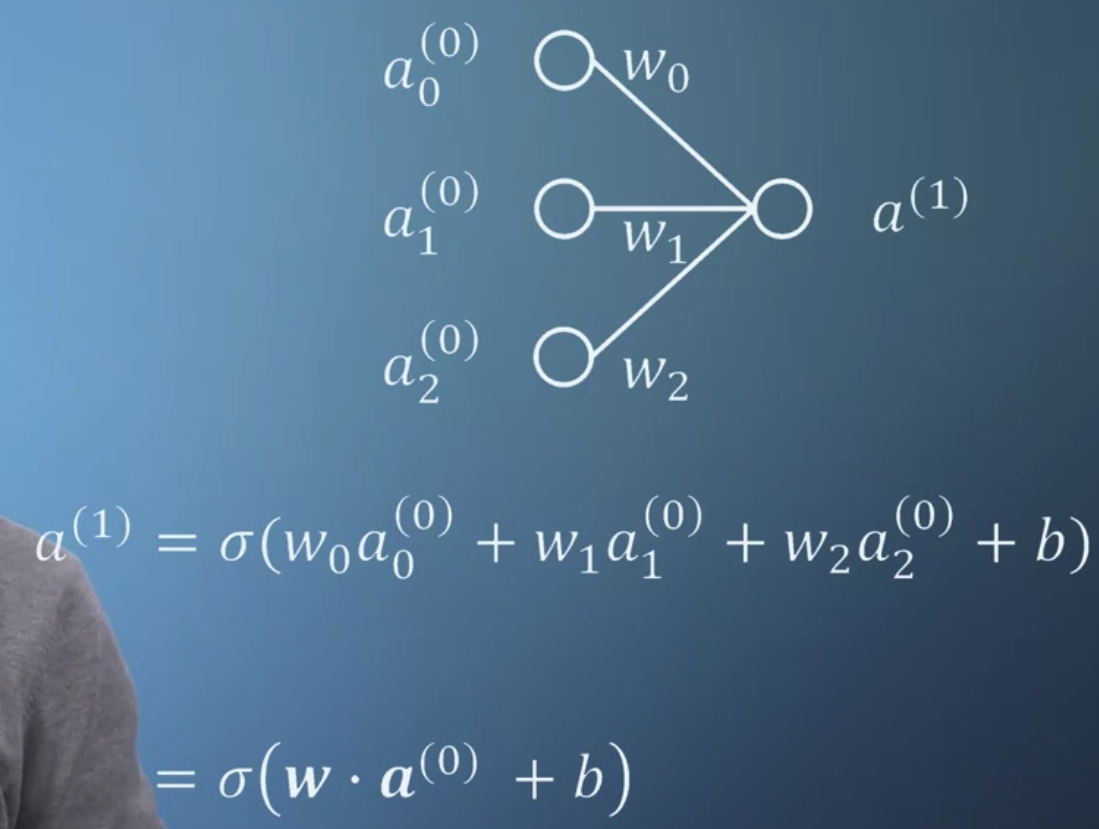

- 만약 입력이 여러개이고 이것이 여러개로 구성된 다음층으로 전달될 때는 위와 같은 구조를 가진다.
- 1번 layer에 속하는 neuron들이 0번 layer에 속하는 neuron들과 모두 연결되어있다.
그리고 그 연결은 위에서 설명한 가중치와의 곱 + 편향으로 구성된다.

- 이를 일반화하면 단순한 숫자(scalar)의 곱이 아닌 벡터의 곱으로 이해할 수 있게 된다.
가중치벡터 W와 입력벡터 a를 곱하고 여기에 편향벡터 b를 더한 결과를 시그모이드 함수에 집어넣는 것이다.
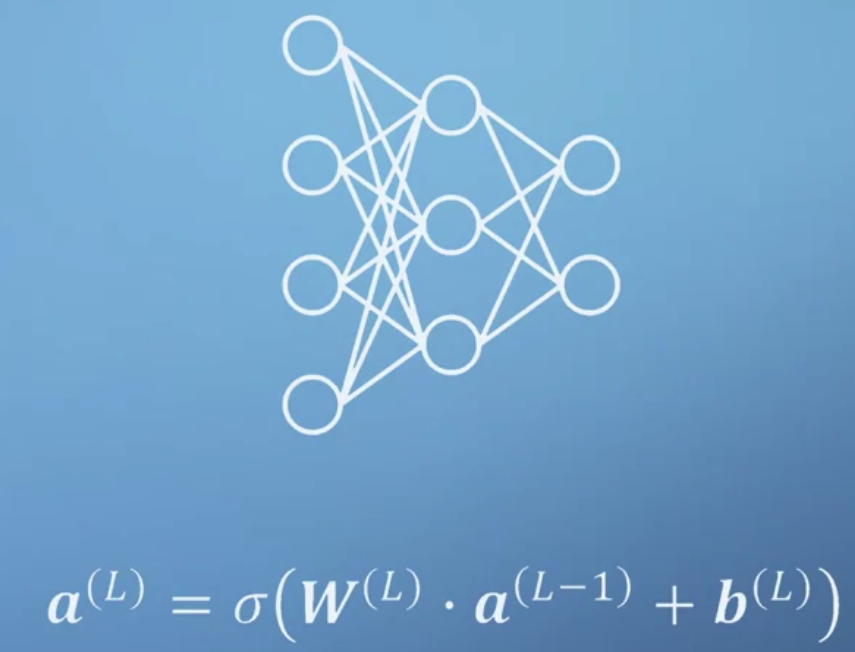
- 다양한 일들을 수행하기 위해서는 layer가 늘어나야 한다.
맨 앞부터 input, hidden, output layer가 된다.
2. Simple Artificial Neural Networks
- 노드 두 개로 구성된 network 학습시키기(1문제)
- 함수를 직접 작동시켜보고 가장 적절한 w,b를 구해야 한다.
- 3개의 노드로 구성된 입력층과 2개의 노드로 구성된 출력층 중 출력층 함수로 구현하기.(1문제)
- (W @ x.T + b.T).T
- Transpose하는 이유를 생각해보자.
- input, hidden, output layer로 구성된 네트워크에서 hidden을 제외하고도 동일하게 유지될까?(1문제)
- No. 가중치와 편향이 의미를 가지기 때문.
- 출력층을 수식으로 표현하기(1문제)
- 가중치, 편향 조작해보면서 시각적으로 이해하기(1문제)
3. More simple neural networks
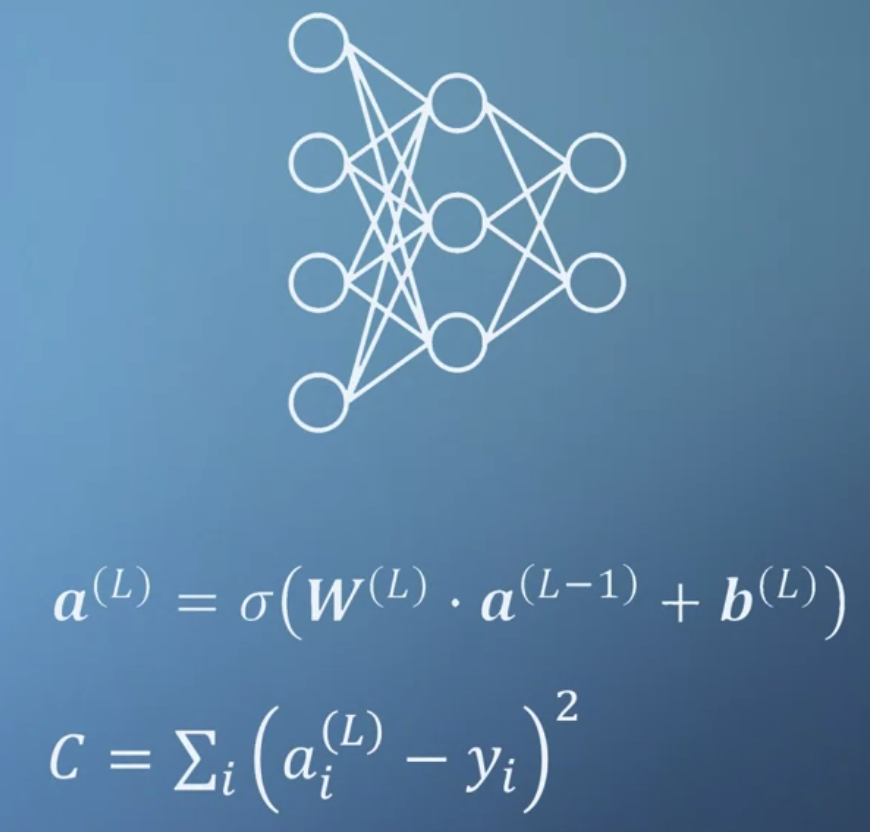
- 여러 개의 입력에 대해 계산된 결과가 hidden layer로 전달되고 이것이 또 계산되어 output이 된다.
- 사실 W와 b는 초기에 의미가 없는 랜덤값이기 때문에 우리가 원하는 결과를 만들어내기 위해서 손실함수를 정의한다.
따라서 이 손실함수의 값이 최소가 되는 것이 우리의 목표가 된다.
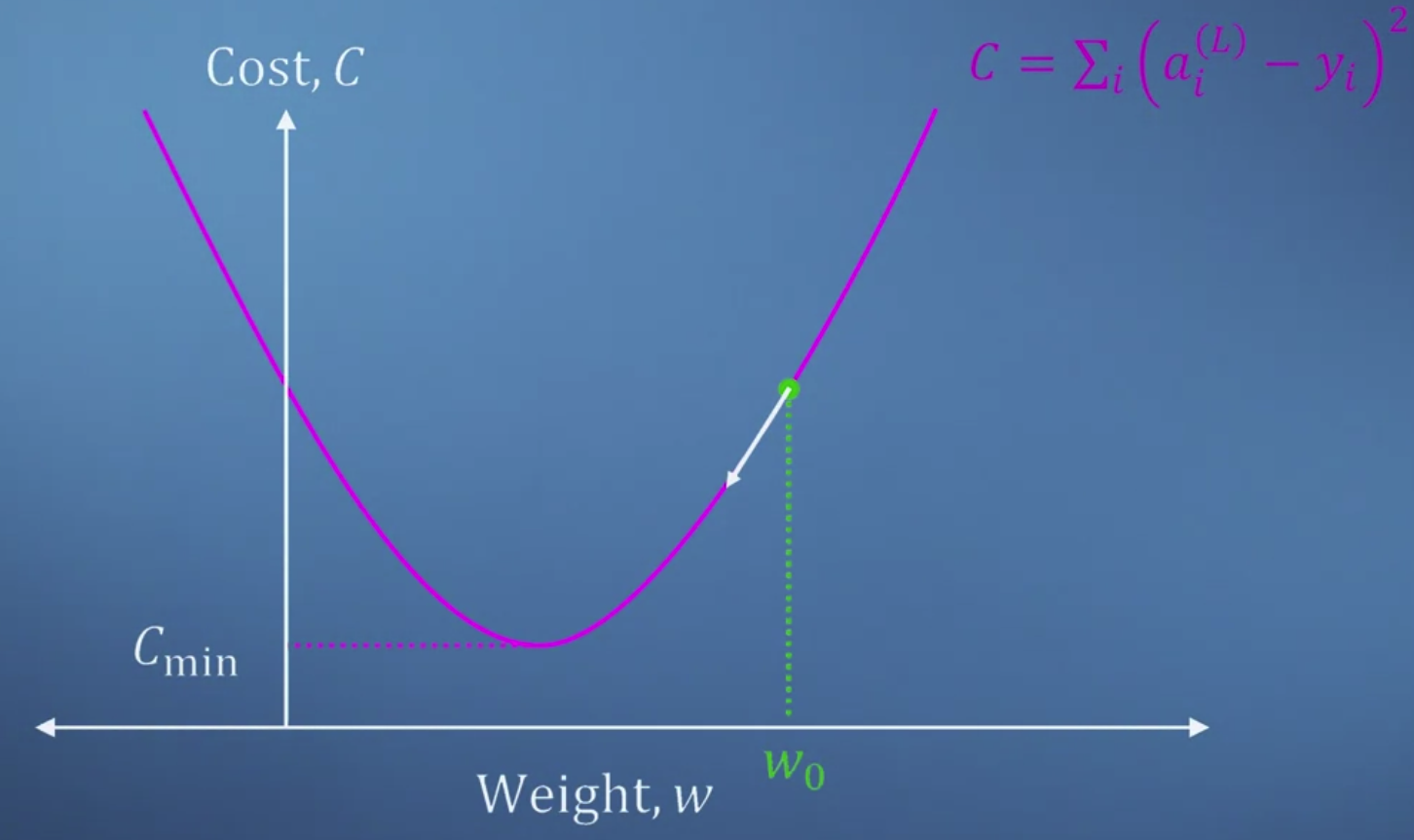
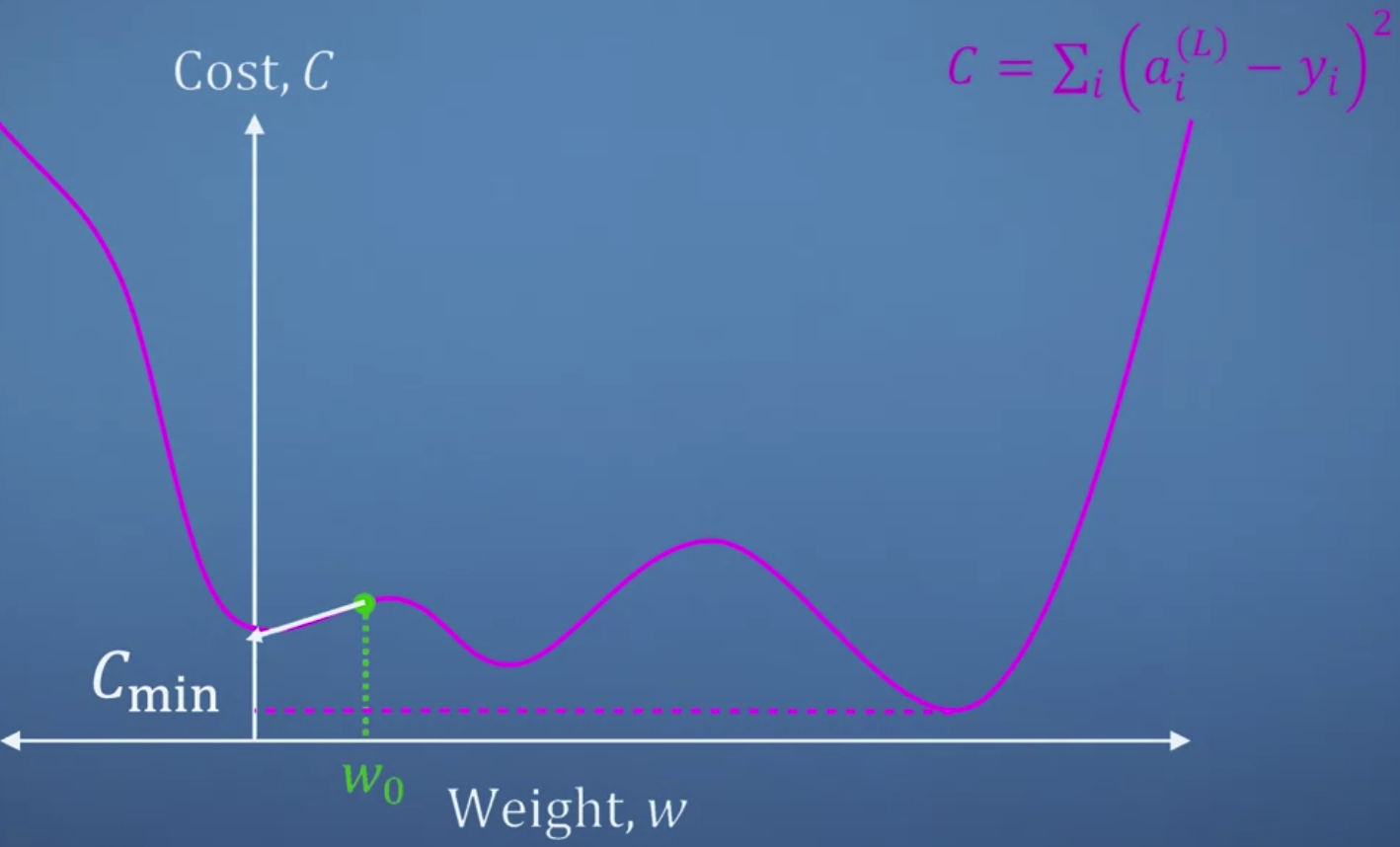
- 가중치와 손실의 관계를 그래프로 표현하면 위와 같다.
손실함수는 우리가 계산한 '추정치'에서 '목표'를 뺀 것의 제곱을 모두 더한 값이 된다.
우리의 목표는 손실이 최소가 되는 지점을 찾는 것이므로 특정 지점에서 구한 미분 계수를 "빼는 방식"으로 가중치를 업데이트 한다.
기울기가 양수인 경우 미분 계수를 빼서 w를 왼쪽으로 보내야 하고,
반대로 기울기가 음수인 경우 미분 계수를 빼서 w를 오른쪽으로 보내야 한다. - 하지만 그래프가 여러 곳에서 움푹 파인 경우 local minimum에 빠지게 된다.
따라서 이때 필요한 것이 Jacobian이다.
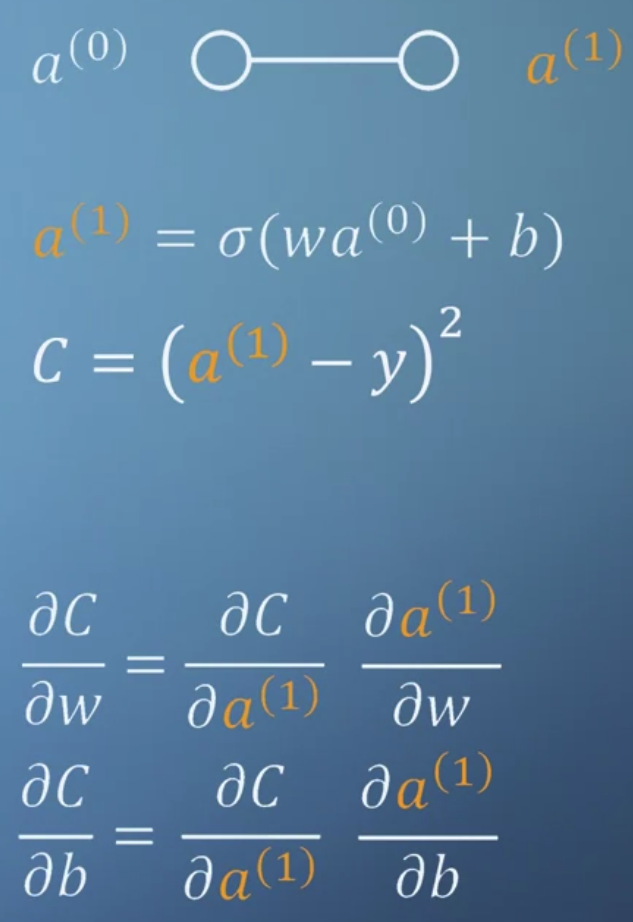
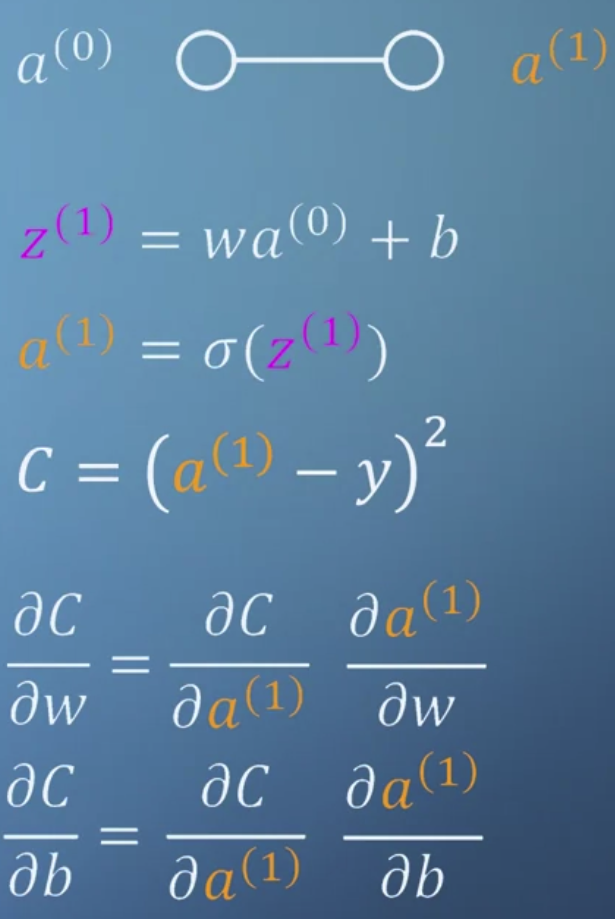

- 위 내용을 종합하여 network를 이처럼 표현할 수 있다.
이때 a를 반복적으로 풀어 쓰는 것보다 wa + b를 z로 치환해서 정리하는 것이 훨씬 깔끔하다. - 결국 chain rule을 적용하여 값을 손실함수를 구하고, 이를 통해 값을 업데이트 하는 것으로 이해할 수 있다.
4. Training Neural Networks
- 코드를 통해 얻어지는 y hat을 보고 손실함수값 구하기(1문제)
- 가중치, 편향으로 이뤄진 cost에 대한 contour graph를 보고 알맞은 내용 고르기(1문제)
- Descending perpendicular to the contours will improve the performance of the network.
- Moving across the contours will get you closer to the minimum valley.
- chain rule을 알맞게 적용한 것 고르기(2문제)
- 코드로 편미분 구현하기(1문제)
- 편향 b를 정의(아주 간단)
- 코드로 알맞은 C 구하기(1문제)
- 입력을 바꿔주면 정답을 구할 수 있다.
5. Backpropagation
- 역전파는 multi-layer로 구성된 networks의 output에서 미분값을 계산해 거꾸로 적절한 w,b를 찾아나가는 과정을 뜻한다.
앞서 배운 내용을 떠올려보면 우리는 cost를 최소화하는 w,b를 구해야한다.
따라서 어떤 입력 x0가 주어졌을 때 이를 w,b를 통해 forward하여 output을 구하고,
그 output을 w0,b0에 대해 미분한 값을 구해야한다. - 하지만 multi-layer에는 여러 변수들이 존재한다.
이 문제에서는 2개의 hidden layer가 존재하고 각각 6,7개의 node가 있다.
어차피 node의 개수는 크게 문제되는 것은 아니고(여기서는) w,b 벡터를 통해 계산결과가 forward된다는 것이 중요하다. - 따라서 output으로부터 기존의 w,b 벡터를 업데이트하기 위해 미분을 수행한다면,
각 단계별로 편미분을 수행하고 그 결과를 곱하는 chain-rule을 적용해야 한다. - 일반적으로 마지막 단계를 제외하면 w,b에 대한 미분 중간 과정은 동일하다.
그렇기 때문에 보통 묶어서 w,b를 업데이트하지만 여기서는 이해도를 높이기 위해 따로 계산하도록 되어있다.
문제에서 설명해주는 그대로 따라서 간단한 코드만 작성하면 문제를 풀 수 있다.
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 3주차' 카테고리의 다른 글
| Chain rule intro. (1) | 2022.10.05 |
|---|
1. Simple neural networks

- neural network를 이루는 작은 원 하나를 neuron이라고 한다.
- 그 구조는 활성화 함수인 시그모이드에 가중치 w와 입력 a를 곱하고 b를 더한 값을 집어넣는 것이다.
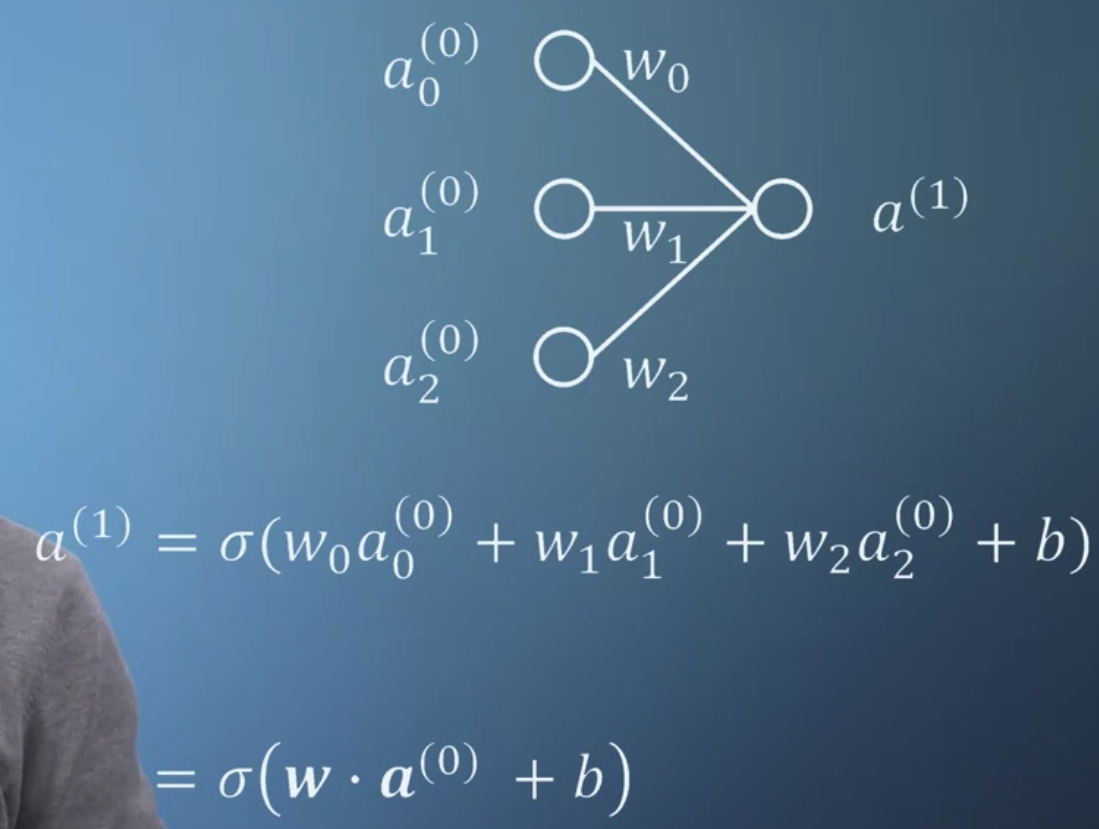

- 만약 입력이 여러개이고 이것이 여러개로 구성된 다음층으로 전달될 때는 위와 같은 구조를 가진다.
- 1번 layer에 속하는 neuron들이 0번 layer에 속하는 neuron들과 모두 연결되어있다.
그리고 그 연결은 위에서 설명한 가중치와의 곱 + 편향으로 구성된다.

- 이를 일반화하면 단순한 숫자(scalar)의 곱이 아닌 벡터의 곱으로 이해할 수 있게 된다.
가중치벡터 W와 입력벡터 a를 곱하고 여기에 편향벡터 b를 더한 결과를 시그모이드 함수에 집어넣는 것이다.
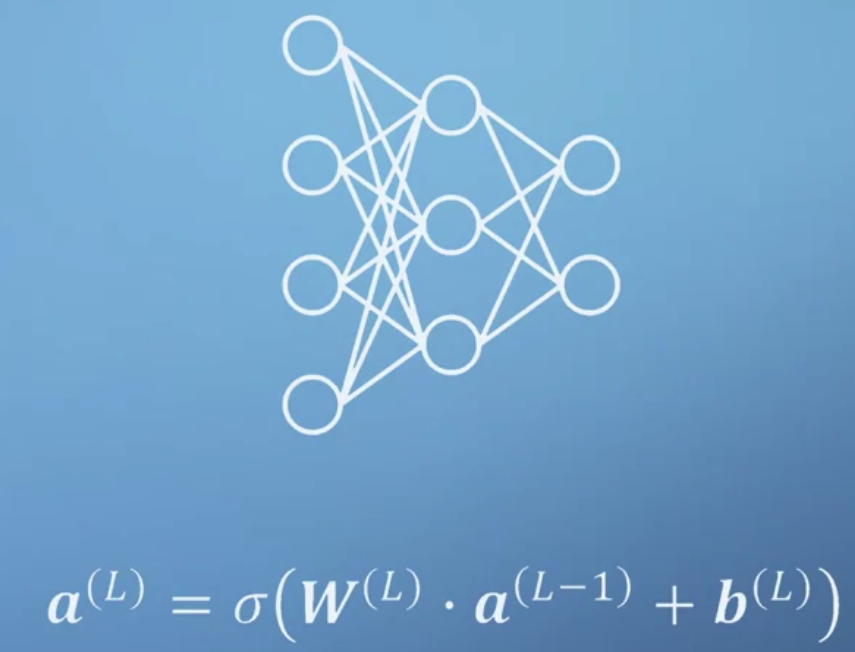
- 다양한 일들을 수행하기 위해서는 layer가 늘어나야 한다.
맨 앞부터 input, hidden, output layer가 된다.
2. Simple Artificial Neural Networks
- 노드 두 개로 구성된 network 학습시키기(1문제)
- 함수를 직접 작동시켜보고 가장 적절한 w,b를 구해야 한다.
- 3개의 노드로 구성된 입력층과 2개의 노드로 구성된 출력층 중 출력층 함수로 구현하기.(1문제)
- (W @ x.T + b.T).T
- Transpose하는 이유를 생각해보자.
- input, hidden, output layer로 구성된 네트워크에서 hidden을 제외하고도 동일하게 유지될까?(1문제)
- No. 가중치와 편향이 의미를 가지기 때문.
- 출력층을 수식으로 표현하기(1문제)
- 가중치, 편향 조작해보면서 시각적으로 이해하기(1문제)
3. More simple neural networks
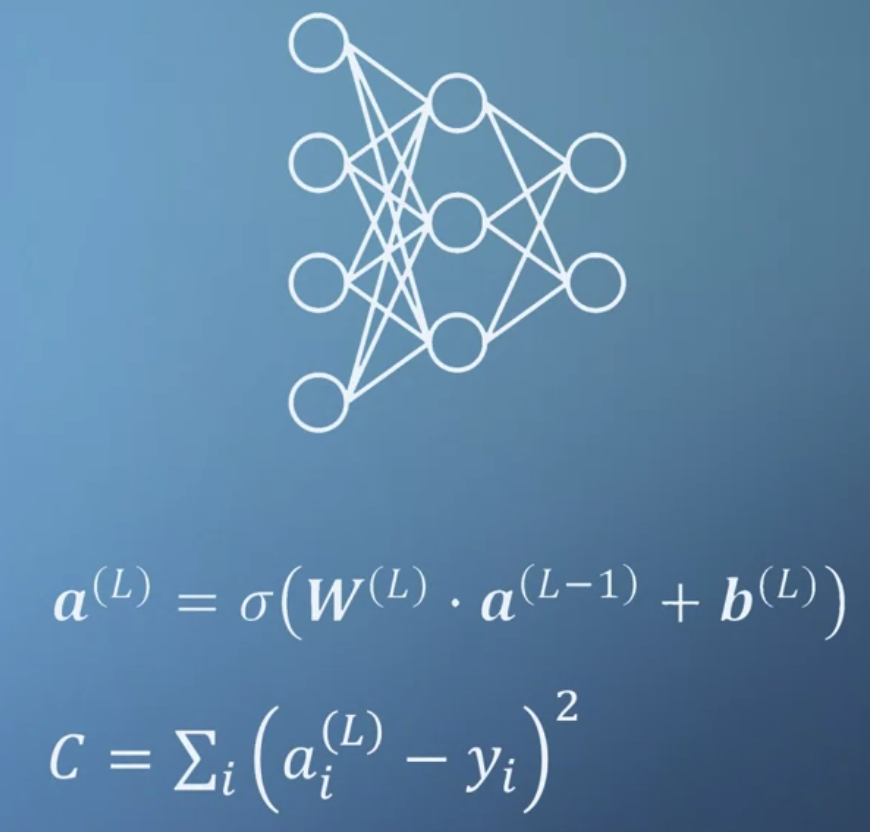
- 여러 개의 입력에 대해 계산된 결과가 hidden layer로 전달되고 이것이 또 계산되어 output이 된다.
- 사실 W와 b는 초기에 의미가 없는 랜덤값이기 때문에 우리가 원하는 결과를 만들어내기 위해서 손실함수를 정의한다.
따라서 이 손실함수의 값이 최소가 되는 것이 우리의 목표가 된다.


- 가중치와 손실의 관계를 그래프로 표현하면 위와 같다.
손실함수는 우리가 계산한 '추정치'에서 '목표'를 뺀 것의 제곱을 모두 더한 값이 된다.
우리의 목표는 손실이 최소가 되는 지점을 찾는 것이므로 특정 지점에서 구한 미분 계수를 "빼는 방식"으로 가중치를 업데이트 한다.
기울기가 양수인 경우 미분 계수를 빼서 w를 왼쪽으로 보내야 하고,
반대로 기울기가 음수인 경우 미분 계수를 빼서 w를 오른쪽으로 보내야 한다. - 하지만 그래프가 여러 곳에서 움푹 파인 경우 local minimum에 빠지게 된다.
따라서 이때 필요한 것이 Jacobian이다.
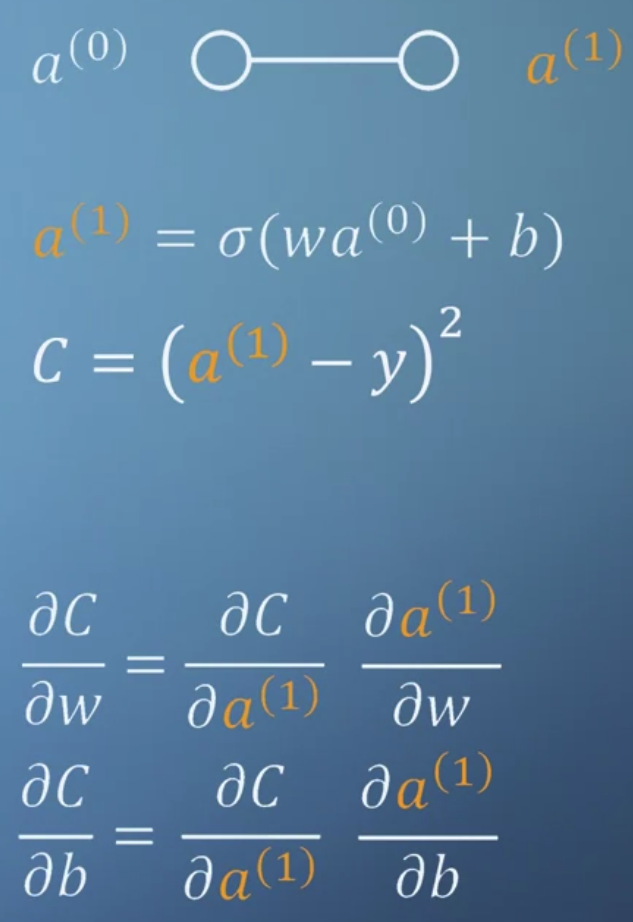
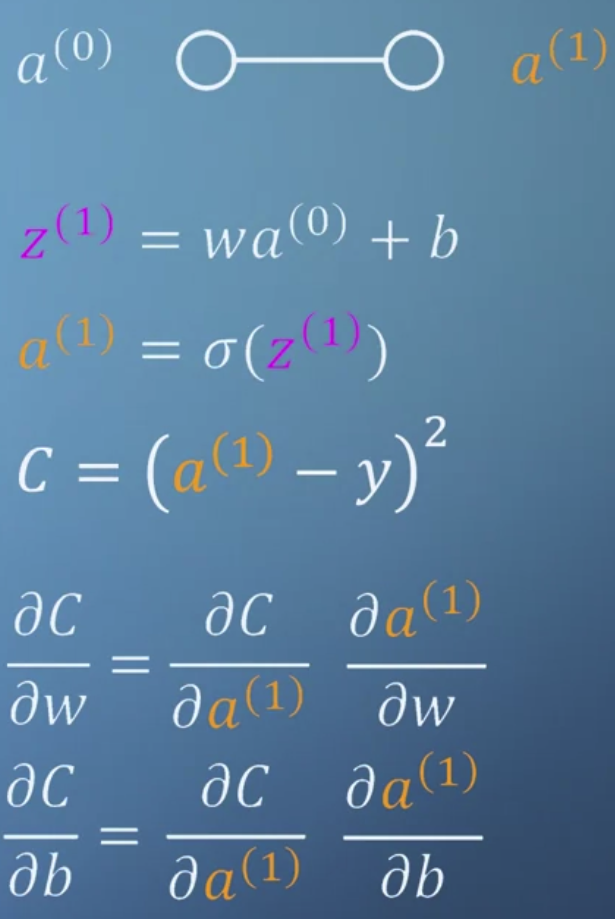

- 위 내용을 종합하여 network를 이처럼 표현할 수 있다.
이때 a를 반복적으로 풀어 쓰는 것보다 wa + b를 z로 치환해서 정리하는 것이 훨씬 깔끔하다. - 결국 chain rule을 적용하여 값을 손실함수를 구하고, 이를 통해 값을 업데이트 하는 것으로 이해할 수 있다.
4. Training Neural Networks
- 코드를 통해 얻어지는 y hat을 보고 손실함수값 구하기(1문제)
- 가중치, 편향으로 이뤄진 cost에 대한 contour graph를 보고 알맞은 내용 고르기(1문제)
- Descending perpendicular to the contours will improve the performance of the network.
- Moving across the contours will get you closer to the minimum valley.
- chain rule을 알맞게 적용한 것 고르기(2문제)
- 코드로 편미분 구현하기(1문제)
- 편향 b를 정의(아주 간단)
- 코드로 알맞은 C 구하기(1문제)
- 입력을 바꿔주면 정답을 구할 수 있다.
5. Backpropagation
- 역전파는 multi-layer로 구성된 networks의 output에서 미분값을 계산해 거꾸로 적절한 w,b를 찾아나가는 과정을 뜻한다.
앞서 배운 내용을 떠올려보면 우리는 cost를 최소화하는 w,b를 구해야한다.
따라서 어떤 입력 x0가 주어졌을 때 이를 w,b를 통해 forward하여 output을 구하고,
그 output을 w0,b0에 대해 미분한 값을 구해야한다. - 하지만 multi-layer에는 여러 변수들이 존재한다.
이 문제에서는 2개의 hidden layer가 존재하고 각각 6,7개의 node가 있다.
어차피 node의 개수는 크게 문제되는 것은 아니고(여기서는) w,b 벡터를 통해 계산결과가 forward된다는 것이 중요하다. - 따라서 output으로부터 기존의 w,b 벡터를 업데이트하기 위해 미분을 수행한다면,
각 단계별로 편미분을 수행하고 그 결과를 곱하는 chain-rule을 적용해야 한다. - 일반적으로 마지막 단계를 제외하면 w,b에 대한 미분 중간 과정은 동일하다.
그렇기 때문에 보통 묶어서 w,b를 업데이트하지만 여기서는 이해도를 높이기 위해 따로 계산하도록 되어있다.
문제에서 설명해주는 그대로 따라서 간단한 코드만 작성하면 문제를 풀 수 있다.
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 3주차' 카테고리의 다른 글
| Chain rule intro. (1) | 2022.10.05 |
|---|
