목차
1. Full derivation of the projection
- 앞의 강의에서 다룬 투영행렬을 구하는 과정이 증명되어있다.
사실 강의에서 이미 그 과정을 보여주었기 때문에 특별한 내용은 없었다.
2. Example: projection onto a 2D subspace

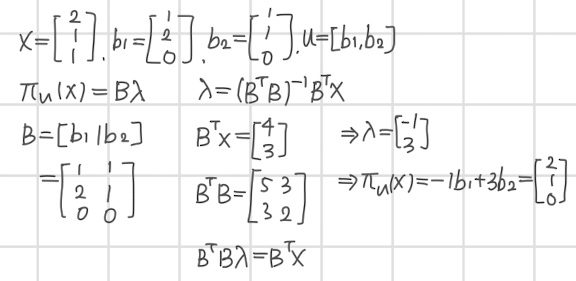
- 3D 공간에 속하는 벡터 x를 2D의 부분공간에 대해 투영한 벡터를 구하는 예시다.
- 결과적으로 투영벡터도 부분공간 u의 기저벡터 b1,b2의 linear combination으로 표현되는 것을 확인할 수 있다.
3. Project 3D data onto a 2D subspace
- 3차원 공간의 벡터 x를 2차원 평면으로 표현되는 부분공간에 대해 내린 투영벡터를 구하는 문제(3개)
- 강의에서 설명된 공식을 잘 이용해야 한다.
- B.T와 B를 곱한 것 vs B.T와 x를 곱한 것을 비교하여 적절한 lambda 벡터를 찾아줘야 한다.
- 만약 projection이 subspace 위에 존재하는 경우 projection에는 어떤 변화도 발생하지 않는다.
4. Orthogonal projections
- 주피터 노트북 환경에서 projection on 1D, 2D를 구현하는 과제
- np.outer( ) - 외적 함수를 사용해야 한다.
이것은 의미상으로 내적(@ / np.dot)과 동일하지만 행렬을 반환하기 때문이다.
즉, 1D에 대해 projection을 구할 때 b @ b.T 를 수행하면 scalar값이 되기 때문에 행렬을 반환하는 외적을 사용하는 것이다. - 그렇기 때문에 n차원에 대해 projection을 구할 때는 굳이 outer 함수를 사용할 필요가 없다.
- np.linalg.norm 함수를 사용하여 벡터의 길이를 구할 수 있다.
projection matrix에 대한 정의에 벡터 b의 norm 제곱이 분모로 들어가는데 여기에 사용하면 된다.
- np.outer( ) - 외적 함수를 사용해야 한다.
출처: Coursera, Mathematics for Machine Learning: PCA, Imperial College London.
'PCA > 3주차' 카테고리의 다른 글
| Projections(1) (0) | 2022.10.07 |
|---|
1. Full derivation of the projection
- 앞의 강의에서 다룬 투영행렬을 구하는 과정이 증명되어있다.
사실 강의에서 이미 그 과정을 보여주었기 때문에 특별한 내용은 없었다.
2. Example: projection onto a 2D subspace

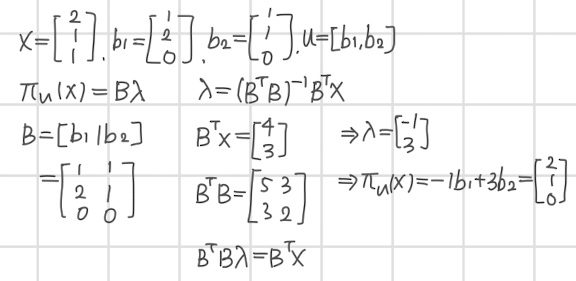
- 3D 공간에 속하는 벡터 x를 2D의 부분공간에 대해 투영한 벡터를 구하는 예시다.
- 결과적으로 투영벡터도 부분공간 u의 기저벡터 b1,b2의 linear combination으로 표현되는 것을 확인할 수 있다.
3. Project 3D data onto a 2D subspace
- 3차원 공간의 벡터 x를 2차원 평면으로 표현되는 부분공간에 대해 내린 투영벡터를 구하는 문제(3개)
- 강의에서 설명된 공식을 잘 이용해야 한다.
- B.T와 B를 곱한 것 vs B.T와 x를 곱한 것을 비교하여 적절한 lambda 벡터를 찾아줘야 한다.
- 만약 projection이 subspace 위에 존재하는 경우 projection에는 어떤 변화도 발생하지 않는다.
4. Orthogonal projections
- 주피터 노트북 환경에서 projection on 1D, 2D를 구현하는 과제
- np.outer( ) - 외적 함수를 사용해야 한다.
이것은 의미상으로 내적(@ / np.dot)과 동일하지만 행렬을 반환하기 때문이다.
즉, 1D에 대해 projection을 구할 때 b @ b.T 를 수행하면 scalar값이 되기 때문에 행렬을 반환하는 외적을 사용하는 것이다. - 그렇기 때문에 n차원에 대해 projection을 구할 때는 굳이 outer 함수를 사용할 필요가 없다.
- np.linalg.norm 함수를 사용하여 벡터의 길이를 구할 수 있다.
projection matrix에 대한 정의에 벡터 b의 norm 제곱이 분모로 들어가는데 여기에 사용하면 된다.
- np.outer( ) - 외적 함수를 사용해야 한다.
출처: Coursera, Mathematics for Machine Learning: PCA, Imperial College London.
'PCA > 3주차' 카테고리의 다른 글
| Projections(1) (0) | 2022.10.07 |
|---|
