Lagrange multipliers

1. Constrained optimisation

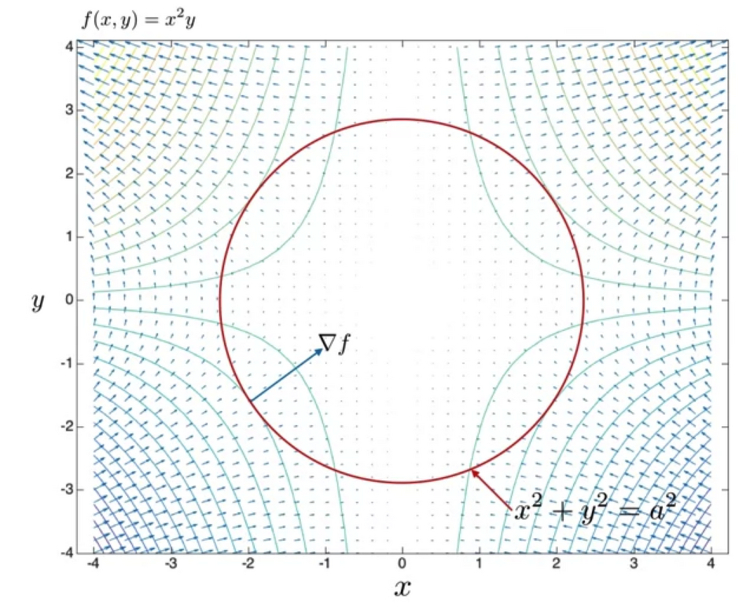
• 이전에 다루었던 함수 f(x,y) = x^2y에 대해서 contour를 생성하면 오른쪽 그림과 같다.
  우리는 gradient vector를 통해 최댓값을 갖는 x,y 지점에 이를 수 있다.
• 이때 최댓값에 이를 수 있는 x,y 쌍의 범위를 원의 형태로 제한(constraint)할 수 있고 이를 함수 g로 표현 가능하다.

 

• 위에서 살펴본대로 f의 값을 최대화하기 위해 제약(constraint) g 함수를 이용할 수 있다.
  이때 두 벡터가 만나는 지점을 구하는 방정식에 Lagrange multiplier가 이용된다.
• 위 방정식을 통해 Lagrange multiplier를 구하고 이를 기존의 식에 다시 대입하여 x와 y의 식을 재구성한다.
• 결과적으로 f를 최대화, 최소화하는 값을 구할 수 있게 된다(x,y가 +-로 각각 두 개이므로 이를 조합한 네 쌍이 solution이 된다).

 

2. Lagrange multipliers

• 이전에 배운 Lagrange multiplier를 실제 구현해보는 과제였다.
• 우선 gradient vector를 구해야 한다.
  따라서 함수 f, g를 각각 x, y에 대해 미분한 결과를 정의한다.
• 그리고 g(x, y) = 0이 되는 지점을 구하는 코드를 실행시켜서 적당한 값을 확인해본다.
• L(x,y,λ)=f(x)−λg(x)

 

3. Optimisation scenarios (Quiz)

• sandpit 게임의 이미지를 가져와서 global minimum으로 converge 할 수 있는 starting point를 고르는 문제가 출제된다.
• 시각화된 자료가 의미하는 내용을 이해하고 정확한 선지를 골라야 한다.

 

 

 

출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.