3.4. LU 분해의 순서
앞 절의 설명한 LU 분해의 순서를 형식적으로 풀어낸 과정

- 분해를 했더라도 L, U를 각각 행렬로서 다루면 메모리를 비효율적으로 사용하게 된다.
비어 있는 장소나 1로 정해져 있는 장소 등은 기록할 필요가 없다.
3.5. LU 분해
정방행렬 A에 대하여
- A = LU 상태로 분해되면 행렬식 det A는 바로 구해진다.

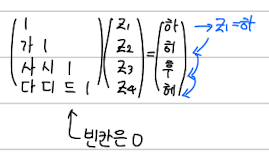
3.6. 일차방정식 LU 분해로 풀다
방향과 계획

푸는 방법
연산량
| 변수소거법 | 가우스 요르단 소거법(Ax = y) | LU 분해 | Lz = y로 풀다 | Ux = z를 풀다 | |
| 나눗셈 | n | n | n | 0 | n |
| 곱셈 | n^3 / 3 | n^3 / 2 | n^3 / 3 | n^2 / 2 | n^2 / 2 |
| 뺄셈 | n^3 / 3 | n^3 / 2 | n^3 / 3 | n^2 / 2 | n^2 / 2 |
- 같은 A에서 여러 가지 y에 대한 Ax = y를 풀 경우에는 한 번 LU 분해해두면 편하다.
출처: 히라오카 카즈유키, 호리 겐, 『프로그래머를 위한 선형대수』, 이창신, 길벗, 2017.
'프로그래머를 위한 선형대수 > 3장' 카테고리의 다른 글
| 3.7. 역행렬을 LU 분해로 구하다 / 3.8. LU 분해의 순서 (2) 예외가 발생한 경우 (0) | 2022.09.13 |
|---|---|
| 3.3. LU 분해 (0) | 2022.09.12 |
| 3.1. 서론 3.2. 준비 운동: 덧셈, 뺄셈, 곱셈, 나눗셈 (0) | 2022.09.12 |
