Stack : resizing-array implementation

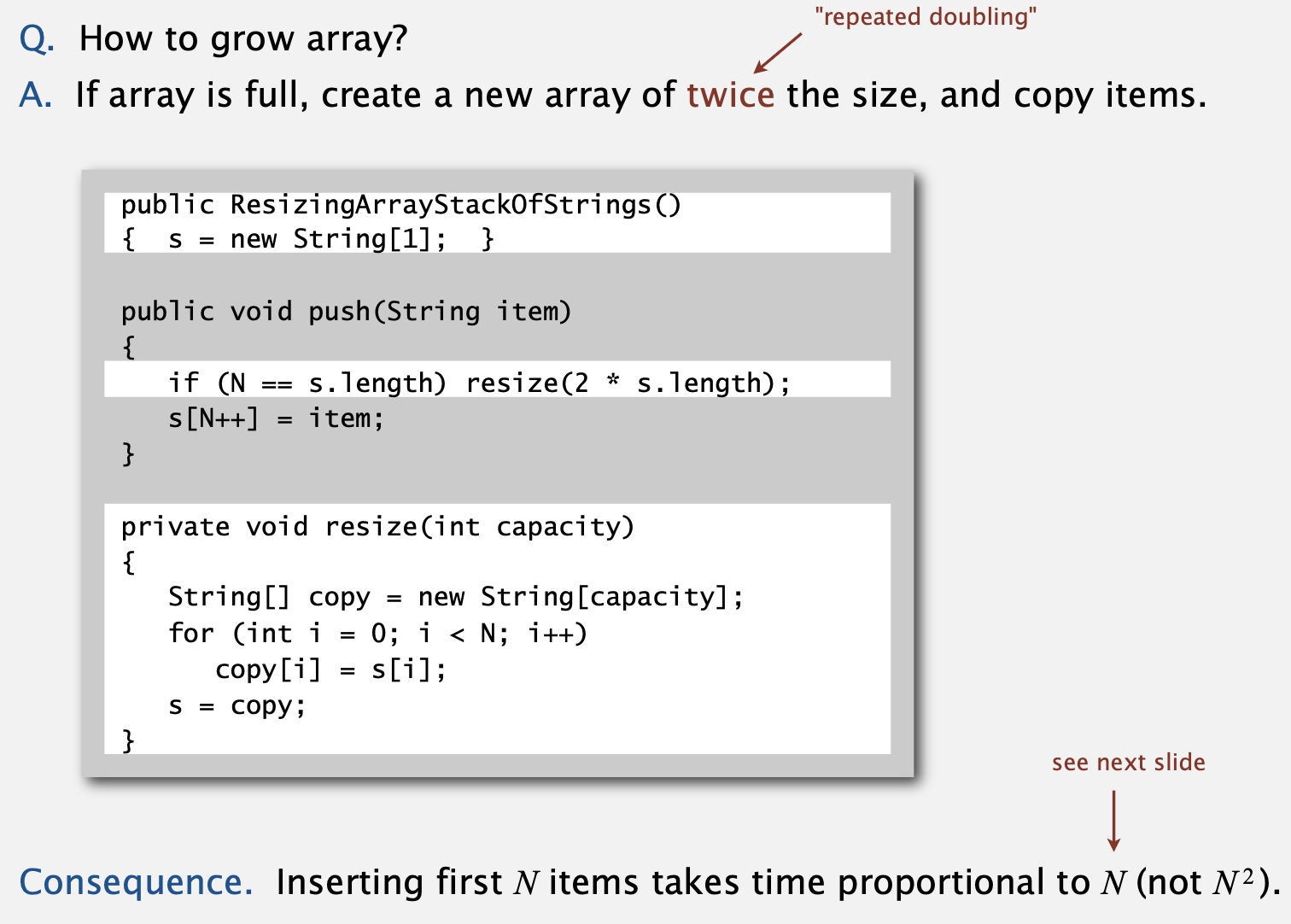
- array의 크기를 재조정하는 것은 아주아주 비효율적인 방식입니다.
왜냐하면 크기를 재조정할 때마다 배열의 모든 아이템을 복사해야 하기 때문이죠.- 이러한 경우 N개의 아이템을 삽입할 때, 총 연산 횟수는 (N^2) / 2이기 때문에 N이 충분히 클 때는 활용 불가능한 방식입니다.
- 따라서 배열의 크기를 매번 재조정하는 것이 아니라, 배열이 꽉 찼을 때만 이를 두 배로 늘리는 방식을 사용합니다.
- 이때는 N개의 아이템을 삽입할 때 N만큼의 시간이 걸립니다.
Stack : amortized cost of adding to a stack
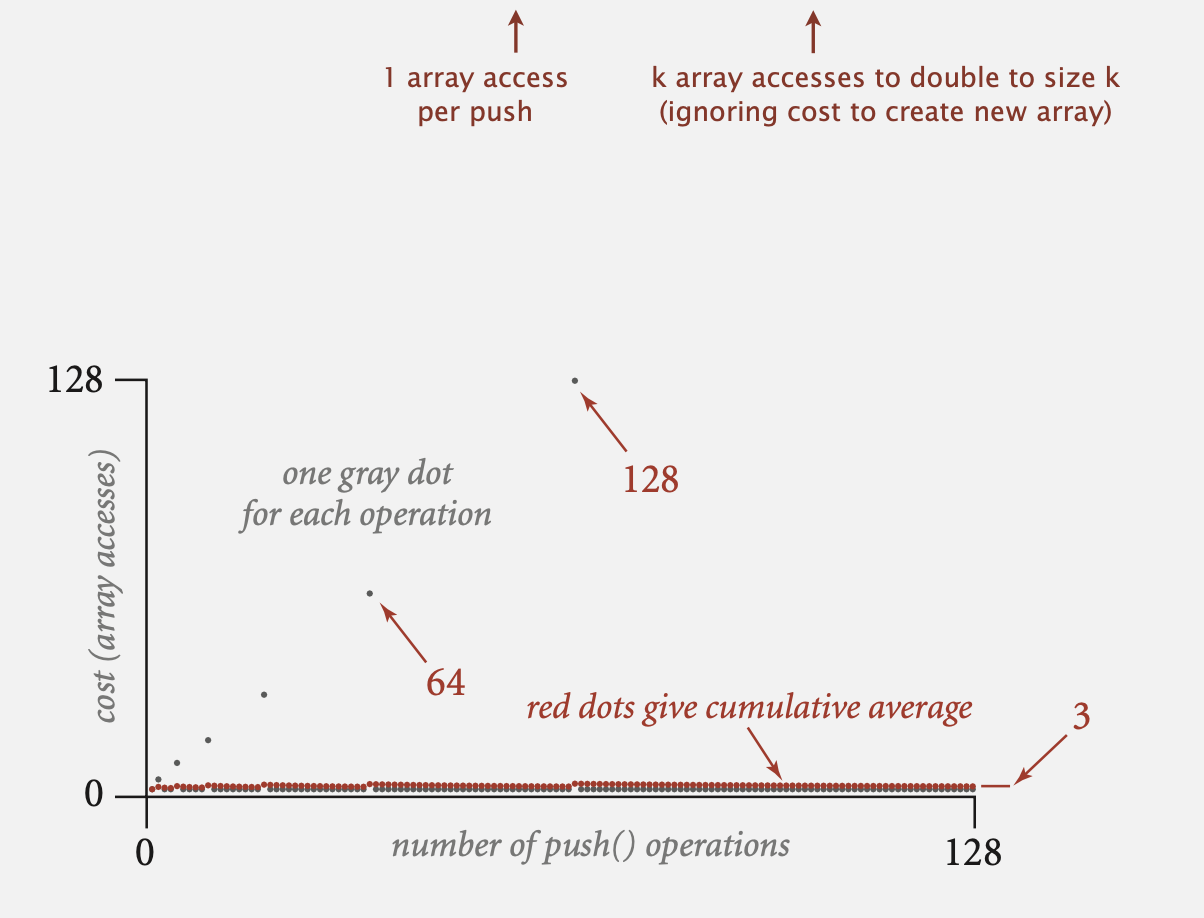
Stack : resizing-array implementation


- 배열의 크기를 줄일 때도, 그 작업을 매번하는 것은 굉장히 비효율적일 것입니다.
따라서 배열 내 비어있는 원소의 개수를 기준으로 배열의 크기를 조정합니다.- 배열 전체의 1/4이 가득 차게 되면 배열을 절반 크기로 줄입니다.
- 원래 N개의 원소가 있었다고 가정하면, 이것이 한 개씩 점점 줄어 1/4개의 원소만 남았을 때 길이를 절반으로 줄이는 것입니다.
- 아래 표에서 언제 배열의 크기가 줄어들게 되었는지 유심히 살펴보면 이해가 쉽습니다.
Stack : resizing-array implementation trace

Stack resizing-array implementation: performance

- 상수의 시간이 걸립니다. M번의 연산에 대해서 M만큼의 시간이 소요됩니다.
Stack resizing-array implementation: memory usage

Stack implementations: resizing array vs. linked list

- 지금까지 stack 구조와 관련해서 살펴본 resizing array 방식과 linked list 방식 중 어떤 것이 더 좋을까요?
이는 요구 사항에 따라 다르다고 합니다.- 만약 최악의 상황에서도 보장된 성능, 처리 시간을 원한다면 linked-list가 좋습니다.
최악의 경우에도 상수 시간이 보장되기 때문이죠. - 하지만 최악의 경우보다도 평균적인 연산 시간에 더 큰 가중치를 두고 있다면 resizing array가 좋습니다.
- 만약 최악의 상황에서도 보장된 성능, 처리 시간을 원한다면 linked-list가 좋습니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 2주차' 카테고리의 다른 글
| Stacks and Queues(6) : Stack and Queue Applications(optional) (0) | 2023.04.12 |
|---|---|
| Stacks and Queues(5) : Iterators (0) | 2023.04.12 |
| Stacks and Queues(4) : Generics (0) | 2023.04.12 |
| Stacks and Queues(3) : Queues (0) | 2023.04.11 |
| Stack and Queues(1) : Stacks (0) | 2023.04.11 |
Stack : resizing-array implementation


- array의 크기를 재조정하는 것은 아주아주 비효율적인 방식입니다.
왜냐하면 크기를 재조정할 때마다 배열의 모든 아이템을 복사해야 하기 때문이죠.- 이러한 경우 N개의 아이템을 삽입할 때, 총 연산 횟수는 (N^2) / 2이기 때문에 N이 충분히 클 때는 활용 불가능한 방식입니다.
- 따라서 배열의 크기를 매번 재조정하는 것이 아니라, 배열이 꽉 찼을 때만 이를 두 배로 늘리는 방식을 사용합니다.
- 이때는 N개의 아이템을 삽입할 때 N만큼의 시간이 걸립니다.
Stack : amortized cost of adding to a stack

Stack : resizing-array implementation


- 배열의 크기를 줄일 때도, 그 작업을 매번하는 것은 굉장히 비효율적일 것입니다.
따라서 배열 내 비어있는 원소의 개수를 기준으로 배열의 크기를 조정합니다.- 배열 전체의 1/4이 가득 차게 되면 배열을 절반 크기로 줄입니다.
- 원래 N개의 원소가 있었다고 가정하면, 이것이 한 개씩 점점 줄어 1/4개의 원소만 남았을 때 길이를 절반으로 줄이는 것입니다.
- 아래 표에서 언제 배열의 크기가 줄어들게 되었는지 유심히 살펴보면 이해가 쉽습니다.
Stack : resizing-array implementation trace

Stack resizing-array implementation: performance

- 상수의 시간이 걸립니다. M번의 연산에 대해서 M만큼의 시간이 소요됩니다.
Stack resizing-array implementation: memory usage

Stack implementations: resizing array vs. linked list

- 지금까지 stack 구조와 관련해서 살펴본 resizing array 방식과 linked list 방식 중 어떤 것이 더 좋을까요?
이는 요구 사항에 따라 다르다고 합니다.- 만약 최악의 상황에서도 보장된 성능, 처리 시간을 원한다면 linked-list가 좋습니다.
최악의 경우에도 상수 시간이 보장되기 때문이죠. - 하지만 최악의 경우보다도 평균적인 연산 시간에 더 큰 가중치를 두고 있다면 resizing array가 좋습니다.
- 만약 최악의 상황에서도 보장된 성능, 처리 시간을 원한다면 linked-list가 좋습니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 2주차' 카테고리의 다른 글
| Stacks and Queues(6) : Stack and Queue Applications(optional) (0) | 2023.04.12 |
|---|---|
| Stacks and Queues(5) : Iterators (0) | 2023.04.12 |
| Stacks and Queues(4) : Generics (0) | 2023.04.12 |
| Stacks and Queues(3) : Queues (0) | 2023.04.11 |
| Stack and Queues(1) : Stacks (0) | 2023.04.11 |
