Shellsort overview

- 정렬을 공부하면서 여러 종류들을 접해봤는데 이건 또 신선하네요..
i 번째 이전의 모든 원소를 살피는 삽입 정렬과 달리 일정 간격(h)만큼과 비교하는 정렬입니다. - 그래서 h 간격에 따라 부분 정렬되어 있습니다.
물론 간격이 1인 경우는 모든 원소가 오름차순으로 정렬되어 있다는 것을 의미하게 됩니다.
h-soring

- 당연한 얘기지만 간격이 크면 부분 정렬된 배열의 크기 자체는 작습니다.
반대로 간격이 작으면 작을수록 배열 전체가 정렬된 상태에 가까워집니다.
Shellsort example: increments 7, 3, 1

Shellsort: intuition

- 그렇다면 이 논리가 어떻게 적용 가능한 것일까요?
바로 작은 간격으로 h 정렬을 수행했을 때도 큰 간격의 h 정렬이 유지되기 때문입니다. - 위 예시에서 보면 7-sort를 적용한 이후 3-sort를 적용해도, 7-sort가 유지되는 것을 볼 수 있습니다.
따라서 간격을 적당히 조절하면서 점점 줄이면 기존의 삽입 정렬보다 효율적으로 정렬을 수행할 수 있습니다.
Shellsort: which increment sequence to use?

- 항상 2를 곱하며 log에 비례하는 연산을 노렸던 것과 달리, 여기서는 3x + 1 항을 사용합니다.
그 이유는 계산하기 쉬워서라고 하네요.
Shellsort: Java implementation

def shell_sort(arr):
n = len(arr)
h = n // 3
while n > 0:
for i in range(h,n):
temp = arr[i]
j = i-h
while j >= 0 and arr[j] > temp:
arr[j+h] = arr[j]
j -= h
arr[j+h] = temp
h //= 3
print(arr)- 정확하게 변환한 것은 아닌데 그래도 얼추 이정도로 변환되는 것 같습니다.
java 코드에서 while문이 중첩되어 있는게 무슨 의미인지 모르겠어서..
Shellsort: visual trace
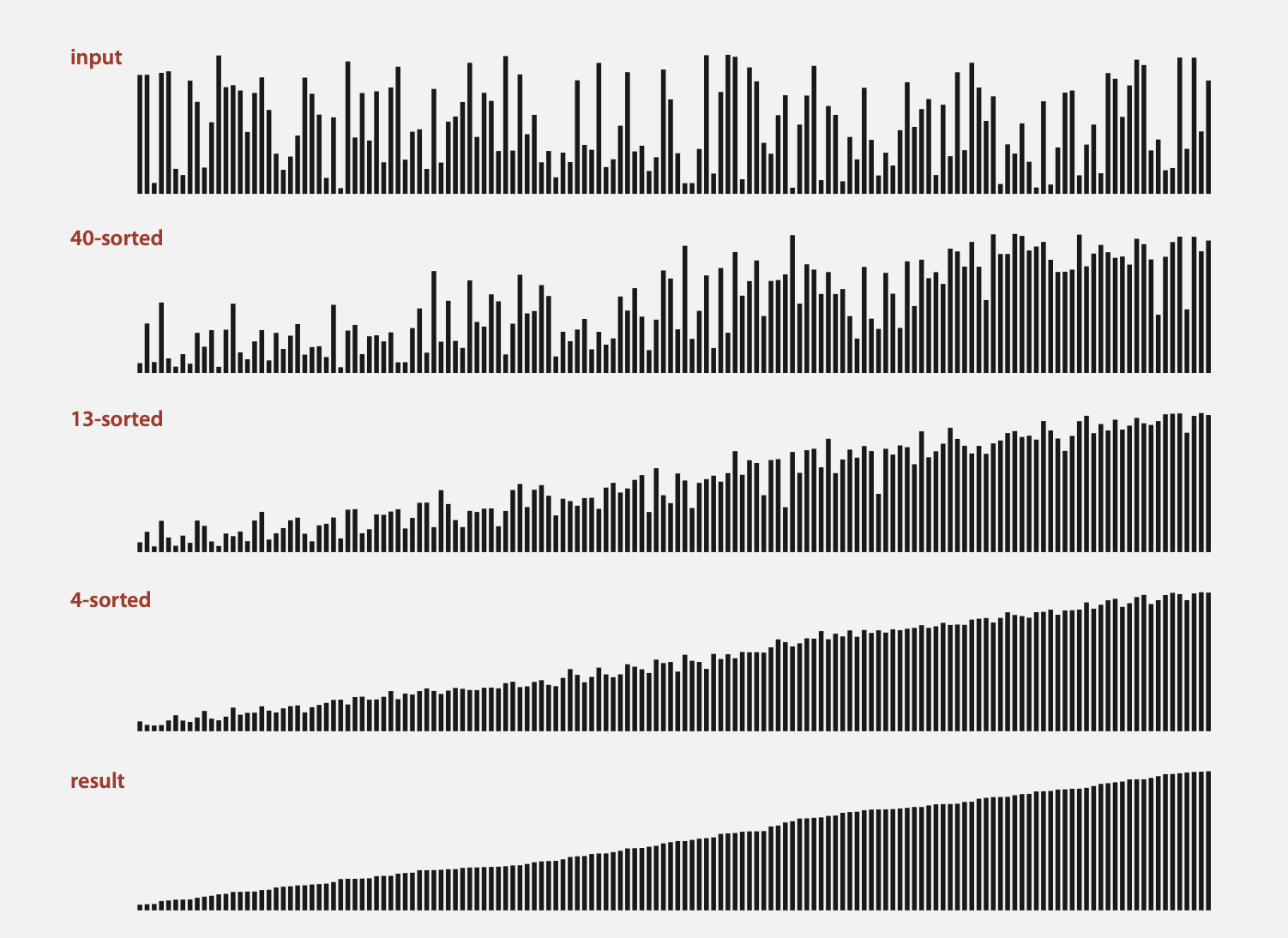
- 위에서 설명한 바와 같이 간격이 작을수록 실제 정렬된 상태 그 자체가 됩니다.
Shellsort: analysis, Why are we interested in shellsort?


- 기존 알고리즘들에 비하면 굉장히 연산 효율이 좋은 정렬이라는 것을 알 수 있습니다.
- 시간 복잡도가 O(N^(3/2))로 기존의 O(N^2)에 비하면 훨씬 낫습니다.
- 결국 배열의 사이즈가 엄청나게 커지더라도 적용 가능한 훌륭한 알고리즘이라고 볼 수 있습니다.
또한 이 정렬을 적용하기 위한 코드도 굉장히 간단하고 짧은 편이라는 것도 장점입니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 2주차' 카테고리의 다른 글
| Elementary Sorts(4) : Convex Hull (0) | 2023.04.18 |
|---|---|
| Elementary Sorts(4) : Shuffling (0) | 2023.04.18 |
| Elementary Sorts(3) : Insertion Sort (0) | 2023.04.17 |
| Elementary Sorts(2) : Selection Sort (0) | 2023.04.17 |
| Elementary Sorts(1) : Sorting Introduction (0) | 2023.04.17 |
