Duplicate keys


일반적으로 대량의 데이터에 대해 정렬을 수행하는 것은 중복되는 key를 기준으로 정렬을 적용하는 경우가 많습니다.
- 위처럼 '도시 - 시간' 형태의 데이터라면 도시를 기준으로 정렬하게 되는 것이죠.
원래는 중복된 key를 포함하는 데이터에 대해 퀵정렬을 수행하는 경우 quadratic(2차) 시간이 걸린다는 문제점이 있었으나,
병합 정렬을 이용하여 그 시간을 획기적으로 줄일 수 있게 되었죠.
Duplicate keys: the problem

하지만 일반적인 병합 정렬 방식을 적용하게 되면, key가 모두 동일한 경우에 대해서는 quadratic 시간이 소요될 것입니다.
이를 방지하기 위해 paritioning item(기준 아이템)과 동일한 것이 확인되는 순간 작업을 멈춰서 NlogN의 시간 복잡도로 단축시킬 수 있습니다.
3-way partitioning


방식은 이와 같습니다.
- lt의 왼쪽에는 lt보다 큰 것을 두지 않는다 = lt가 가장 큰 값으로 유지되도록 한다.
- gt의 오른쪽에는 gt보다 작은 것을 두지 않는다 = gt가 가장 작은 값으로 유지되도록 한다.
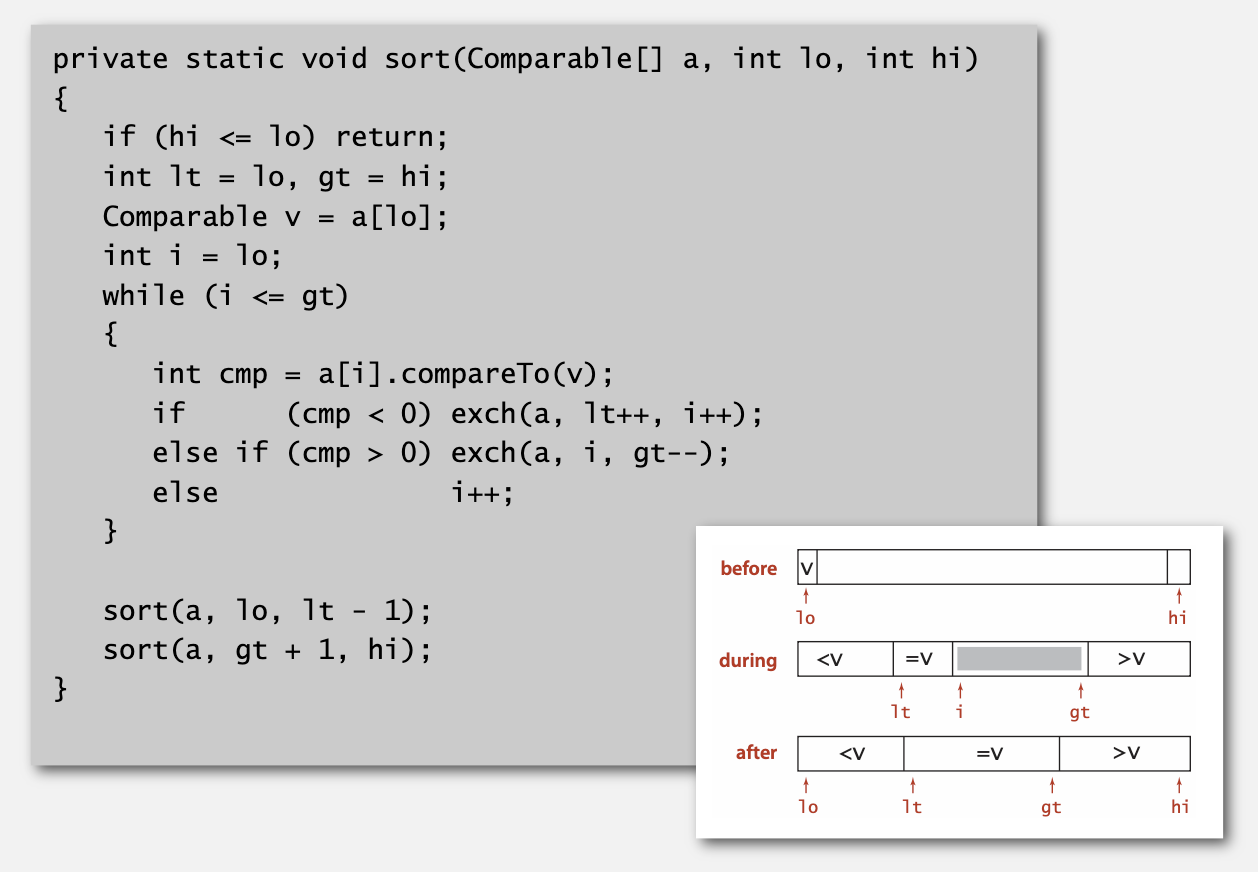
다익스트라 방식으로 코드화하면 우측과 같습니다.
- 스캔 대상 a[i]가 구분 기준 v = a[lo] 보다 작은 경우 : lt와 i를 교환하고 둘을 증가시킵니다.
- lt보다 큰 것은 lt의 왼쪽에 위치할 수 없기 때문입니다.
- 스캔 대상 a[i]가 구분 기준 v보다 작은 경우 : gt와 i를 교환하고 gt를 감소시킵니다.
- gt보다 작은 것은 gt의 오른쪽에 위치할 수 없기 때문입니다.
- 스캔 대상 a[i]가 구분 기준 v와 동일한 경우 : i만 증가시킵니다.
Dijkstra's 3-way paritioning: trace

3-way quicksort: Java implementation
def exch(a, i, j):
a[i], a[j] = a[j], a[i]
def sort(a, lo, hi):
if hi <= lo:
return
lt, gt = lo, hi
v = a[lo]
i = lo
while i <= gt:
cmp = (a[i] > v) - (a[i] < v) # Java's a[i].compareTo(v)
if cmp < 0:
exch(a, lt, i)
lt += 1
i += 1
elif cmp > 0:
exch(a, i, gt)
gt -= 1
else:
i += 1
sort(a, lo, lt - 1)
sort(a, gt + 1, hi)다른 부분은 그냥 파이썬 문법에 맞게 코드를 작성한 것이라 특별할 것은 없고 compareTo를 구현한 부분만 눈여겨 보면 될 것입니다.
대상 객체 a[i]와 인자 v를 비교하고 있습니다.
- 둘이 동일한 경우 0을 반환합니다.
- a[i] > v인 경우 1-0이 되어 1(양수)을 반환합니다.
- a[i] < v인 경우 0-1이 되어 -1(음수)을 반환합니다.
Duplicate keys: lower bound

결론을 말하자면 3-way partitioning은 다양한 분야의 어플리케이션의 시간 복잡도를 선형로그(linearithmic, NlogN)을 선형(linear)시간으로 단축시켜줄 수 있다는 것입니다.
이를 자세히 증명하는 것은 수업의 범위를 벗어나는 것으로 다루지 않는다고 합니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 3주차' 카테고리의 다른 글
| Quicksort(4) : System Sorts (0) | 2023.04.25 |
|---|---|
| Quicksort(2) : Selection (0) | 2023.04.21 |
| Quicksort(1) : Quicksort (0) | 2023.04.21 |
| Mergesort(4),(5) : comparators, stability (0) | 2023.04.20 |
| Mergesort(3) : Sorting Complexity (0) | 2023.04.20 |
