union find

Union-find applications 네.. 뭐.. 이렇게 다양한 분야에 Union-Find 알고리즘이 사용될 수 있다고 하네요! Percolation 과제로 제시되는 문제는 percolation(여과, 투과)입니다. N * N 사이즈의 격자판이 존재합니다. p의 확률로 격자가 오픈되어 있고, 1-p의 확률로 격자가 닫혀있습니다. 격자의 맨 위부터 아래까지 연결되면 percolate라고 판정합니다. 이 알고리즘은 전기, 유동 액체, 사회적 상호작용 등에 적용 가능한 알고리즘이라고 합니다. Likelihood of percolation 공간이 open / closed(1-open) 될 확률에 따라 시스템이 percolate 할지 안할지 달라지겠죠. p의 값을 조정하면서 그 결과가 어떻게 되는지를 시각..

Improvement 1: weighting 기존의 quick-union의 속도 문제를 개선하기 위한 weighted quick-union입니다. 더 큰 트리가 위에 위치합니다. 즉, 작은 트리가 아래에 위치합니다 → worst case를 방지할 수 있습니다. 작은 트리의 루트를 큰 트리의 루트와 연결합니다. 우측의 그림은 기존의 union과 weighted 방식으로 개선된 union의 결과를 도식화 한 것입니다. Weighted quick-union: Python implementation class Weighted_Quick_Union_UF(n): id = [x for x in range(n)] sz = [1 for _ in range(n)] # tree 내 원소 개수 def root(i): whil..

Quick-union [lazy approach] 이번엔 id 배열이 인덱스별로 root 노드를 가리키고 있습니다. 여기서 인덱스와 id 배열의 값이 동일한 것은 자기 자신이 곧 노드라는 뜻입니다. 따라서 p와 q가 연결되어 있는지는 두 노드의 root 노드가 동일한지를 비교하면 됩니다. root 노드를 찾아가는 과정은 재귀적입니다. root 노드의 root가 자기 자신이 될 때까지 과정을 반복하게 됩니다. 여기서 id 배열의 값을 업데이트 할 때는 관련된 모든 값을 변경할 필요가 없습니다. 단지 child가 되는 node의 root를 변경해주면 되는 것입니다. 마찬가지로 python 코드로 구현한 결과물은 다음과 같습니다. class Quick_Union_UF(n): id = [x for x in ra..

Quick-find [eager approach] 지난 시간부터 이어지는 개념을 생각해봅시다. 주어진 7개의 union에 따라 10개의 숫자들은 위와 같은 연결 구조를 띕니다. id라는 배열에서 같은 값을 지닌 인덱스들이 동일한 connected component에 속하는 것입니다. 예를 들어 0, 5, 6은 모두 값이 0이므로 같은 곳에 속하죠. 만약 두 개의 component를 union하면 어떻게 될까요? 기존의 값들을 모두 바꿔줘야 하기 때문에 번거롭습니다. 지금 예시에서는 1과 6을 연결하는데, 0, 5, 6 모두 값을 변경해야 하죠. 그렇기 때문에 두 object를 union할 때 진즉에 관련된 모든 값을 변경하는 방식을 취할 수도 있습니다. 관련된 코드는 자바로 작성되는데, 저는 자바를 잘 ..

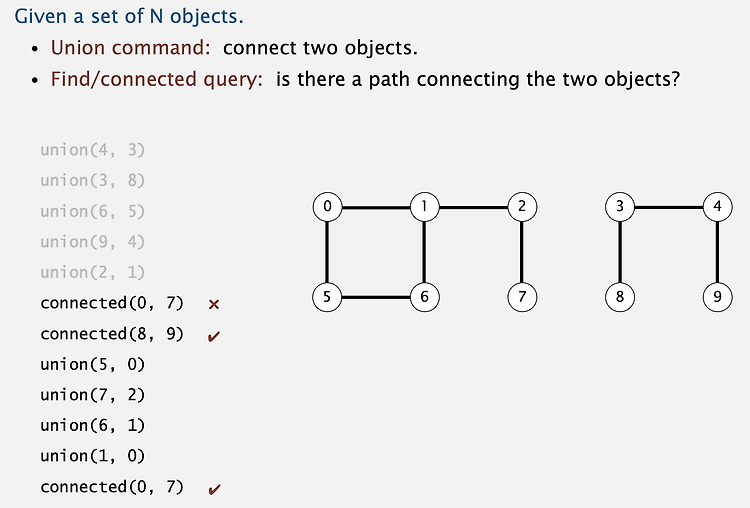
Dynamic Connectivity Union Find 알고리즘을 이해하기 위해서는 Dynamic Connectivity에 대한 기본 개념이 필요합니다. union : 두 object를 연결합니다. connected : 두 object가 연결되어 있는지에 대해 응답합니다. 초기 세팅에 의하면 0과 7은 연결되어 있지 않습니다. 하지만 다른 object들이 연결됨에 따라 두 object 또한 간접적으로 연결되게 되었습니다. Modeling the connections is connected to, 즉 연결되었다는 표현은 크게 세 가지를 포함할 수 있습니다. 1) Reflexive : 자기 자신에게는 항상 연결되어 있는 셈이죠. 2) Symmetric(대칭적) : p가 q에 연결되어 있다면, q도 p에 연..