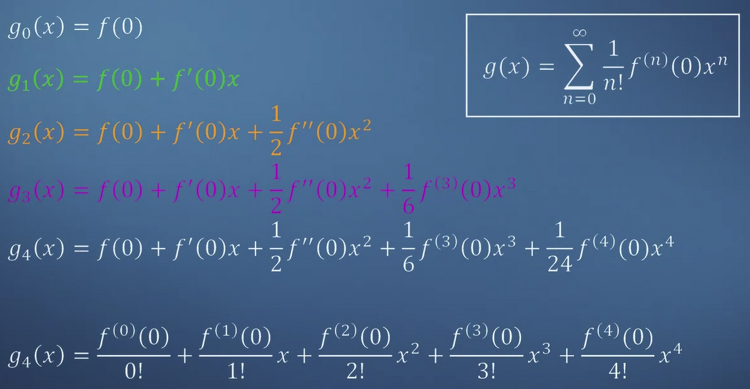Taylor series for approximations(1)

1. Building approximations

1) 이 cooking book을 읽는 사람과 내가 비슷한 오븐을 쓴다고 가정

2) 치킨도 비슷하다고 가정

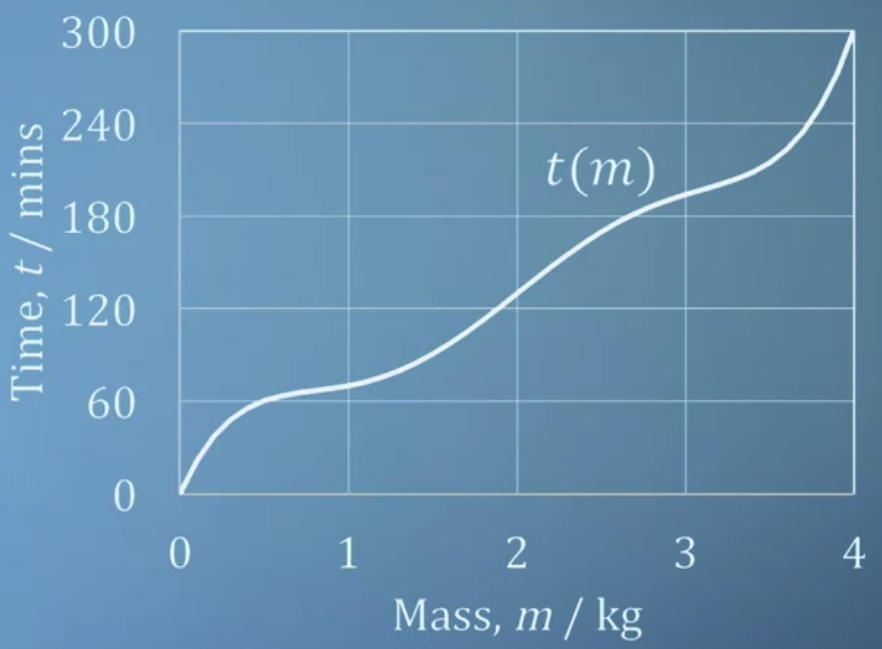
• 다른 조건들이 유사하다고 가정하면 변수들을 줄일 수 있고 이를 통해 간단한 식으로 근사할 수 있게 된다.

 

 

2. Power series

Truncated series

주어진 함수 g의 변수를 하나씩 늘려나가면서 기존의 그래프와 얼마나 유사한지 확인하고 있다.

변수를 늘릴수록 기존의 그래프와 유사해지는 것을 볼 수 있다.

이런 방식으로 쭉 늘어놓은 함수의 모음을 truncated series라고 부른다.

 

 

3. Matching functions and approximations (Quiz)

• 기존의 그래프를 보고 적절한 근사를 고르는 문제들이 출제되어 있다.
  또한 주어진 근사가 몇 번째 근사인지 맞히거나 제대로 근사를 하고 있는게 맞는지 검증하는 문제도 있다.
  문제 난이도 자체는 높지 않아 보이는데 어떤 근거와 논리로 정답을 고르는지 전혀 알 수가 없었다.

 

4. Power series derivation

• 특정 point에서의 모든 정보(이를테면 함수값, 1차 미분계수, 2차 미분계수, etc)를 알면 어떤 함수를 재구성하는데 이 정보들을 사용할 수 있다.
• contininous하고 원하는 만큼 differentiate할 수 있어야 한다는 특징이 있다. -> well behaved

 

1개의 정보(함수값)만을 사용한 g0, 함수값과 미분계수(2개의 정보)를 사용한 g1

• 함수값, 1,2차 미분계수를 사용한 g2
• 계산을 통해 구한 1,2차 미분계수를 그대로 사용하여 식을 재구성했음을 알 수 있다.

 

이전의 식에서 3차의 계수(coefficient)만 구하면 된다.

 

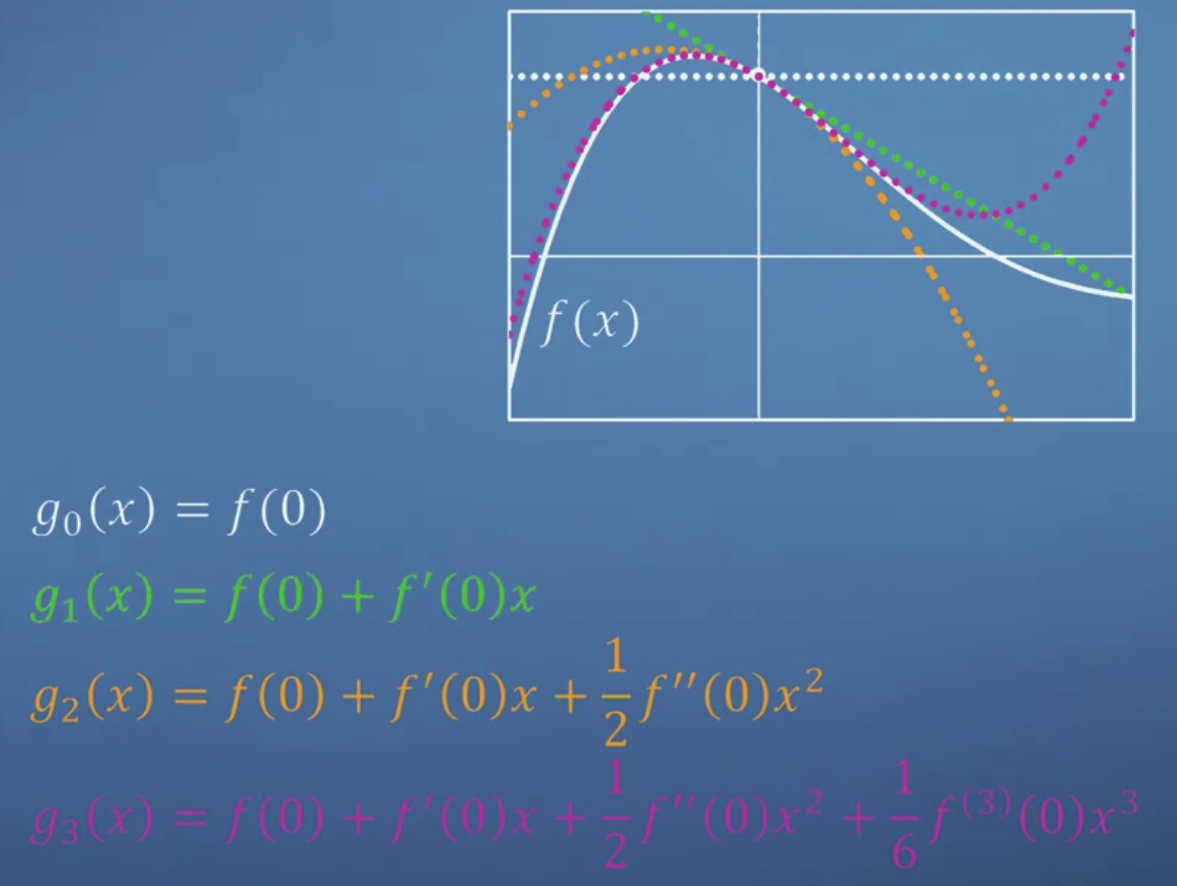
• 지금까지의 과정을 통해 4차의 계수가 어떻게 계산될지는 쉽게 짐작할 수 있다.
• 이와 같은 계산 패턴을 우리는 factorial로 표현할 수 있고, 이를 일반화하면 1/n!에 f를 n번 미분한 결과를 곱하여 모두 더한 것으로 이해할 수 있게 된다.
• 이를 Maclaurin series라고 한다. x = 0에서의 모든 것을 알 수 있으면 재구성이 가능하다.

 

 

 

출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.