1. Simple linear regression
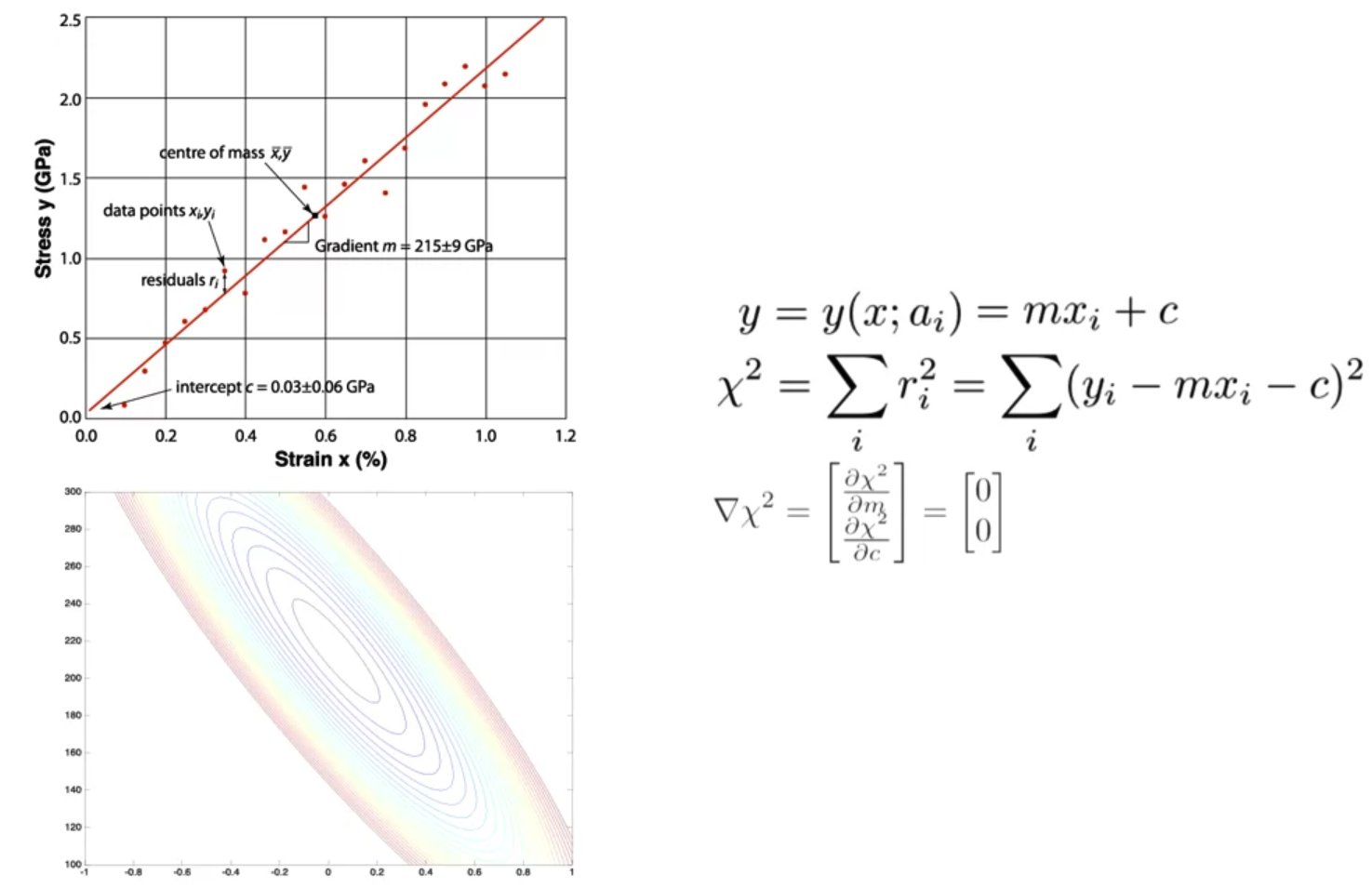
- 어떤 데이터들을 잘 설명하는 직선을 구할 수 있다.
데이터들을 기반으로 어떤 직선이 데이터의 분포를 가장 잘 표현할 수 있는지에 대해 고민하는 것이다. - 이 직선으로 예측된 값이 실제값과 얼마나 떨어져있는지 확인하기 위한 식이 카이제곱이다.
실제값에서 예측값을 빼서 제곱한 값들을 모두 더한 것이 된다.
이 값이 곧 오차(loss)를 의미하게 되고 이를 최소화해야 우리가 원하는 최적의 직선을 얻을 수 있게 된다. - 결국 이 오차를 끝까지 최소화하면 그 값은 0이 될 것이다.
따라서 카이제곱을 구성하는 변수인 m과 c에 대해 편미분을 수행하여 카이제곱벡터를 구하고,
이것이 영벡터와 같아지는 때가 언제인지 구하면 된다.
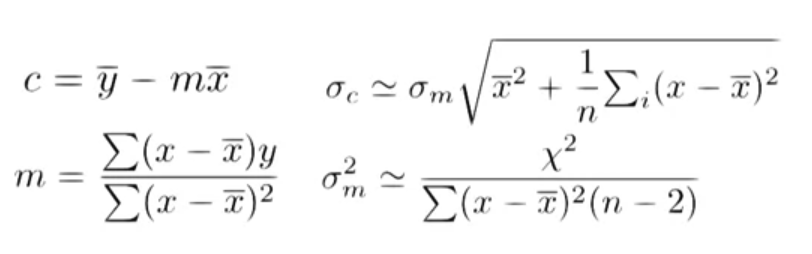
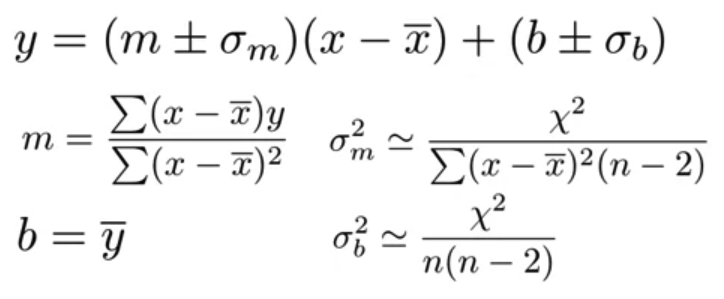
- 위 과정에서 c와 m에 대한 식을 정리할 수 있게 되고, 이를 통해 각 변수에 대한 표준편차를 정리할 수 있다.
그리고 그 결과를 우리가 추정하여 얻고자 하는 식 y에 적용한다.
2. Linear regression (Quiz)
- 데이터의 분포를 보고 linear regression에 적합한지 아닌지 고르기
- 그냥 직선의 형태로 표현될 수 있는 데이터의 분포를 고르면 된다.
- 카이제곱에 사용되는 m과 c를 numpy를 이용한 코드로 구현하기
m = (np.sum(np.dot((xdat-xbar),ydat))) / (np.sum(np.dot((xdat-xbar),(xdat-xbar))))
c = ybar - np.dot(m,xbar)- np.sum, np.dot 함수를 이용하여 m, c를 정의대로 구현할 수 있다.
이렇게 코드로 구현하면 실제 오차를 구하기 위해 손으로 직접 계산할 필요가 없어진다. - 하지만 이런 것도 사실 정의할 필요 없이 특정 라이브러리의 함수를 이용하여 한번에 처리할 수 있다.
scipy의 stats에는 linregress라는 함수가 있는데, x data, y data를 argument로 받아서 slope m, intercept c를 반환해준다.
regression = stats.linregress(xdat,ydat)
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 6주차' 카테고리의 다른 글
| Non-linear regression (0) | 2022.10.23 |
|---|
1. Simple linear regression

- 어떤 데이터들을 잘 설명하는 직선을 구할 수 있다.
데이터들을 기반으로 어떤 직선이 데이터의 분포를 가장 잘 표현할 수 있는지에 대해 고민하는 것이다. - 이 직선으로 예측된 값이 실제값과 얼마나 떨어져있는지 확인하기 위한 식이 카이제곱이다.
실제값에서 예측값을 빼서 제곱한 값들을 모두 더한 것이 된다.
이 값이 곧 오차(loss)를 의미하게 되고 이를 최소화해야 우리가 원하는 최적의 직선을 얻을 수 있게 된다. - 결국 이 오차를 끝까지 최소화하면 그 값은 0이 될 것이다.
따라서 카이제곱을 구성하는 변수인 m과 c에 대해 편미분을 수행하여 카이제곱벡터를 구하고,
이것이 영벡터와 같아지는 때가 언제인지 구하면 된다.
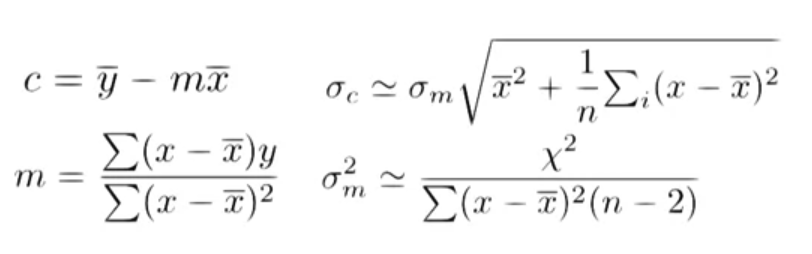
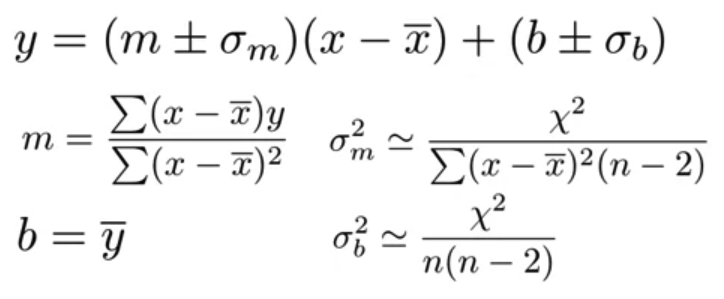
- 위 과정에서 c와 m에 대한 식을 정리할 수 있게 되고, 이를 통해 각 변수에 대한 표준편차를 정리할 수 있다.
그리고 그 결과를 우리가 추정하여 얻고자 하는 식 y에 적용한다.
2. Linear regression (Quiz)
- 데이터의 분포를 보고 linear regression에 적합한지 아닌지 고르기
- 그냥 직선의 형태로 표현될 수 있는 데이터의 분포를 고르면 된다.
- 카이제곱에 사용되는 m과 c를 numpy를 이용한 코드로 구현하기
m = (np.sum(np.dot((xdat-xbar),ydat))) / (np.sum(np.dot((xdat-xbar),(xdat-xbar))))
c = ybar - np.dot(m,xbar)- np.sum, np.dot 함수를 이용하여 m, c를 정의대로 구현할 수 있다.
이렇게 코드로 구현하면 실제 오차를 구하기 위해 손으로 직접 계산할 필요가 없어진다. - 하지만 이런 것도 사실 정의할 필요 없이 특정 라이브러리의 함수를 이용하여 한번에 처리할 수 있다.
scipy의 stats에는 linregress라는 함수가 있는데, x data, y data를 argument로 받아서 slope m, intercept c를 반환해준다.
regression = stats.linregress(xdat,ydat)
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 6주차' 카테고리의 다른 글
| Non-linear regression (0) | 2022.10.23 |
|---|
