Non-linear regression

1. General non linear least squares

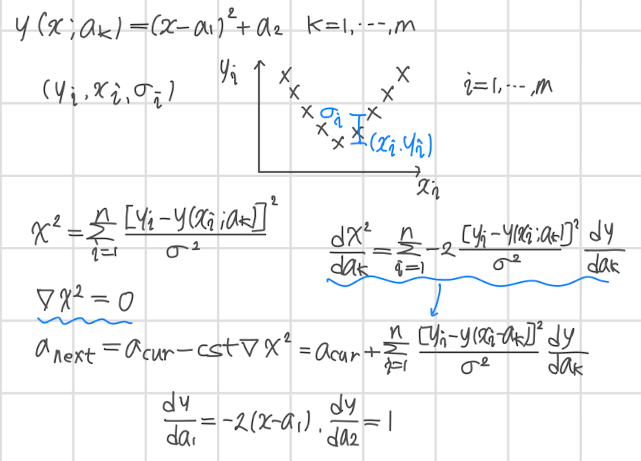
• non-linear function의 최솟값을 찾는 과정을 식으로 전개하면 위와 같다.
  이때도 마찬가지로 loss에 해당하는 카이제곱을 구해야한다.
  그러나 변수가 여러 개이므로 주어진 y식을 각 변수에 대해 편미분한 결과를 파악해두어야 한다.
• linear regression를 수행할 때와 마찬가지로 카이제곱 벡터가 0이 될때까지 기존의 값에서 카이제곱의 미분한 결과를 반복적으로 빼주어야 한다.
  이때 dy / da_k는 y가 a1, a2로 구성된 식이므로 이를 계산하기 전 식을 나타내고 있다.

 

 

2. Fitting a non-linear function (Quiz)

• 비선형 함수를 적용할 수 있는 데이터 분포 고르기
• 카이제곱 식에 대해 올바른 설명 고르기
  • 우리의 목표는 카이제곱을 0으로 만들어(최소화해서) 최적의 함수를 구하는 것이다.
  • parameter X를 제곱하는 것은 불확실성의 부정적 효과를 최소화하기 위함이다.
• 카이제곱, Jacobian, Gaussian distribution의 식 구하기
  • 편미분을 올바르게 적용해서 답안을 골라야 한다.
  • 지수함수에 대해 편미분을 수행할 때는 합성함수를 미분할때의 규칙을 적용하면 된다.

 

3. Fitting the distribution of heights data (Assignment)

• numpy를 이용하여 다변수로 함수의 최적화를 구현하는 과제.
  특정 함수가 주어졌을 때 이를 편미분한 결과를 코드로 구현해야 한다.
• 과제에서는 mu, sigma에 대해 편미분을 수행하도록 되어있었다.
  따라서 두 변수를 각각 Jacobian의 element로 구성하고 이를 이용하여 값을 업데이트하면 된다.

 

 

 

출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.