Finding the size of a vector, its angle, and projection

1. Modulus & inner product

 

벡터를 단위벡터로 표현하기

• 벡터는 length(길이)와 direction(방향)을 가진다.
• 단위벡터 i,j 로 벡터 r을 표현할 수 있다.

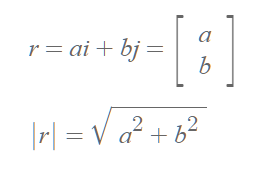
• i 와 j 의 상수배를 제곱하고 루트를 씌우면 r의 크기(길이)가 된다. 이는 피타고라스 정리에 의한 것이다.

 

Inner(dot) product 정의하기(내적)

• 내적은 inner product, dot product, scalar product, projection product 등 다양하게 불린다.
• 두 벡터 r, s 가 있을 때 innder product는 다음과 같이 정의된다.

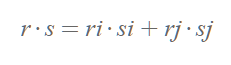
• 결과값은 벡터가 아닌 스칼라다.

 

벡터의 성질 세 가지

​1) commutative (교환법칙 성립)

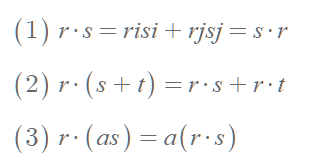
2) distribute over addtion (덧셈에 대해 분배법칙 성립)

3) associative over scalar multiplication (스칼라곱에 대해 결합법칙 성립)

 

 

link between dot product and the length or modulus of a vector (내적과 벡터 길이의 관계)

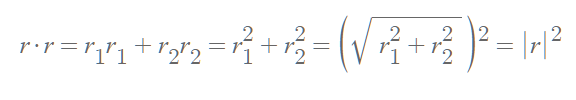
• 벡터의 size를 알고 싶으면 벡터 자신과 내적을 시키고 루트를 씌우면 된다.

 

 

2. Cosine & dot product

 

코사인 법칙으로 내적의 의미 파악하기

​

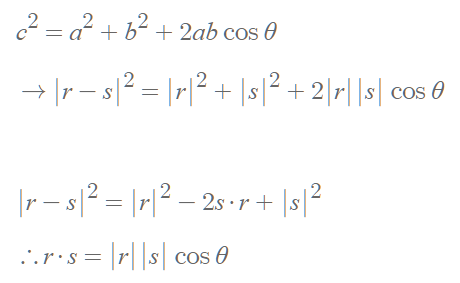
• 벡터 r, s의 내적(dot product)은 두 벡터의 크기(size)와 두 벡터 사이의 각을 곱한 값으로 표현된다.

 

cos θ 로 확인할 수 있는 세 가지 방향

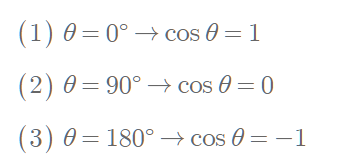
1) 두 벡터 사이의 각이 0도라는 것은 두 벡터의 방향이 같다는 것을 의미한다.

 따라서 두 벡터의 내적은 각 벡터의 크기의 곱이 된다.

 

2) 두 벡터 사이의 각이 90도라는 것은 두 벡터가 서로 직교 혹은 수직한다고 표현한다.(orthogonal or perpendicular to each other)

 두 벡터는 만날 수 없는 방향으로 가게 되므로 cos θ = 0이 되어 두 벡터의 내적은 0이 된다.

 

3) 두 벡터 사이의 각이 180도라는 것은 두 벡터가 정반대 방향을 가리킨다는 것을 의미한다.

 이때 cos θ = -1이 되어 두 벡터의 내적은 각 벡터의 크기의 곱에 음수를 취한 값이 된다. 음수는 벡터에서 방향을 나타내므로 두 벡터가 정반대라는 정보를 담게 된다.

 

요약

• 두 벡터의 내적은 '각 벡터의 크기의 곱 * cos 끼인 각'으로 표현된다.
• 따라서 내적은 벡터의 크기와 두 벡터 간 방향 정보를 담고 있는 것이다.

 

 

3. Projection

 

Scalar projection

• 삼각함수(sohcahtoa)의 cosine 정의를 이용하여 projection을 구한다.

 

 

출처 : Wikipedia

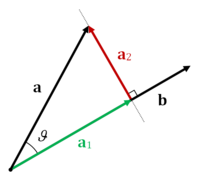
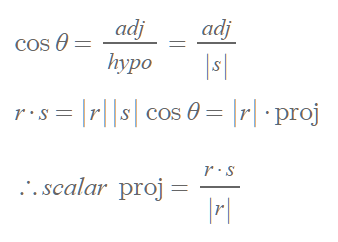
• adj = adjacent(인접변), hypo = hypothenus(빗변)
• cosine의 정의에 따라 벡터 r에서 벡터 s에 내린 사영(projection)을 구할 수 있다. 두 벡터의 내적을 한 벡터의 크기로 나눈 값이 되는데, 내적또한 scalar 값이므로 이 결과값도 scalar값이 된다. 따라서 이를 scalar projection이라고 부른다.
• 내적을 projection product라고 부르는 이유이기도 하다.

 

Vector projection

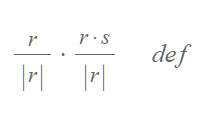
• 사영의 크기는 위에서 구한 scalar projection임을 알 수 있다.(s벡터가 r벡터에 내린 수선)
• 벡터 r을 r의 크기로 나누게 되면 순수하게 방향만 가지고 있는 벡터가 된다(r 방향을 가리키는 unit vector). 따라서 이 식은 '사영의 방향' * '사영의 크기'로 이해할 수 있다.
• 벡터 r을 제외한 벡터의 크기, 벡터 r,s의 내적은 전부 scalar 값이다. 따라서 벡터 한 개와 scalar 의 곱으로 표현된 것이므로 결과값은 벡터가 된다. 따라서 이를 vector projection이라고 부른다.

 

 

4. Dot product of vectors(Quiz 4)

 

벡터의 크기, 내적 구하기(2문항)

 

scalar / vector projection 구하기(2문항)

• s onto r, r onto s 는 다른 결과가 나온다.

 

벡터의 크기 대소비교(1문항)

• 두 벡터의 크기를 따로 구하여 더한 것이 두 벡터를 합친 것의 크기보다 크다.
• 항상 성립하는 명제인지는 모르겠다. 적어도 따로 구한 것이 합친 것 이상일 것이다.

 

내적(dot product)의 설명으로 옳은 것은?(1문항)

• 벡터의 크기는 자기 자신과 내적한 것이다.
• 내적을 이용하여 두 벡터 사이의 각을 구할 수 있다.(내적의 정의)
• 벡터 r에 대한 벡터 s의 사영 벡터는 'r 방향의 유닛 벡터 x scalar 벡터(크기)'로 표현된다.

 

 

 

출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London