1. Changing basis
Coordinate System(좌표계)
- 벡터는 기저 벡터의 합으로 표현된다.
- 이 벡터를 다른 기저 벡터의 합으로 표현할 수 있다.
단, 이 기저 벡터들은 서로 직교해야 한다(orthogonal to each other)
직교하는 vector에 대해 내적(dot product) 취해보기
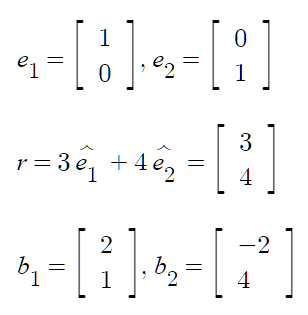
- 기저벡터 e1, e2로 벡터 r을 표현
- 또다른 기저벡터 b1,b2

- scalar projection을 구하고 여기에 b1, b2의 방향벡터를 곱해서 vector projection을 구한다.
- 벡터 r이 기저벡터 b1, b2로 표현되는 것을 확인했다.
요약
- vector는 우리가 지금 표현하는 axes에 묶여있는 것이 아니다.
- basis vector는 data의 공간을 표현한다.
- 위처럼 어떤 벡터를 다른 기저벡터로 표현이 가능한 경우는 다른 기저벡터가 서로 orthogonal(직교)할 때이다.
2. Changing basis(Quiz 5)
벡터 v를 기저벡터 b로 표현하는 문제 5개
- 2차, 3차, 4차에 대해서 각각 계산
- scalar projection에 방향 벡터를 곱해 vector projection을 구하면 된다.
- 사실상 scalar projection만 구하면 정답이 된다. 서로 직교한다는 전제가 있기 때문이다.
3. Basis, vector space, and linear independence
Linearly Independent
- Basis(기저)는 서로 선형독립 관계에 있다.
- 기저로 만들어지는 공간(span)에 들어간 기저의 개수 n은 곧 차원의 개수가 된다(n-dimensional)
정의 및 성질
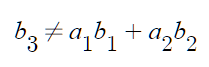
- 임의의 숫자 a1, a2에 대해 위 식을 만족하는 경우 b3는 b1, b2와 선형독립이다.
- 이는 b3가 span(b1, b2) 위에 놓여있지 않음을 의미한다.
- b3는 unit vector(길이가 1인 벡터)가 아니다.
- 또한 다른 벡터와 직교(orthogonal)하면 안 된다.
4. Applications of changing basis
직선으로 표현 가능한 그래프의 예
- x, y 축을 기준으로 여러 데이터들을 점으로 찍고, 이를 관통하는 직선이 있다.
- 점들이 이 직선으로부터 떨어진 거리를 noise라고 볼 수 있다.
- 두 가지 방식(벡터)로 표현할 수 있다.
1) har far along the line
2) har far from the line
두 벡터와 noise 간의 관계
- 이것도 마찬가지로 기저벡터(단위벡터)를 바꾼 것으로 이해할 수 있다.
(이때 변경된 기저벡터는 orthogonal to each other) - 이런 식으로 어떤 벡터의 표현 방식을 바꾸는 것은 실제 data science와 machine learning 분야에서 흔하다.
ex) 픽셀 데이터 → 특징값(눈, 코, 입 등)
5. Linear dependency of a set of vectors
- 선형 독립/종속을 확인하는 간단한 예제 5개
- 선형종속임을 증명할 수 있는 상수 구하기
6. Vector operations assessment
- standard basis를 기준으로 표현된 vector를 다른 basis를 기준으로 표현하기 (2문항)
이때 그 크기(vector projection의 길이)를 구하는 문제도 포함 (1문항) - 주어진 세 개의 열벡터가 선형독립인지 아닌지 판별하기 (1문항)
- 벡터의 덧셈 (1문항)
출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
'Linear Algebra > 2주차' 카테고리의 다른 글
| Finding the size of a vector, its angle, and projection (0) | 2022.09.07 |
|---|
