Two classic sorting algorithms

- 지금까지 배웠던 정렬들과 달리, 앞으로 배울 두 정렬인 '병합 정렬'과 '퀵 정렬'은 엄청나게 효율적이고 지금까지도 널리 쓰이는 공신력 있는 알고리즘입니다.
Mergesort

- 병합 정렬의 기본 아이디어는, 배열을 반으로 쪼개고 그 결과를 합치는 작업을 재귀적으로 반복하는 것입니다.
Abstract in-place merge demo

- 캡쳐본이라 영상이 아니지만, 방법은 이렇습니다.
우선 맨 처음의 배열을 복사한 aux 배열을 생성합니다. - 그리고 이를 반으로 쪼개어 왼쪽의 첫 번째, 오른쪽의 첫 번째 원소에 인덱스 i, j 를 부여합니다.
그리고 오리지날 배열의 첫 번째 인덱스는 k가 됩니다. - i, j 를 비교하여 더 작은 것을 k 자리에 넣고 k는 1 증가합니다.
그리고 i와 j 중에서 k 자리에 들어간 것에 1을 더합니다. - 위 예시의 경우 A가 E보다 더 작으므로 j가 k에 들어가고 j += 1 이 됩니다.
그리고 E, C를 비교하면 C가 더 작으므로 또 j += 1 이 되는 것입니다.
Merging: Java implementation
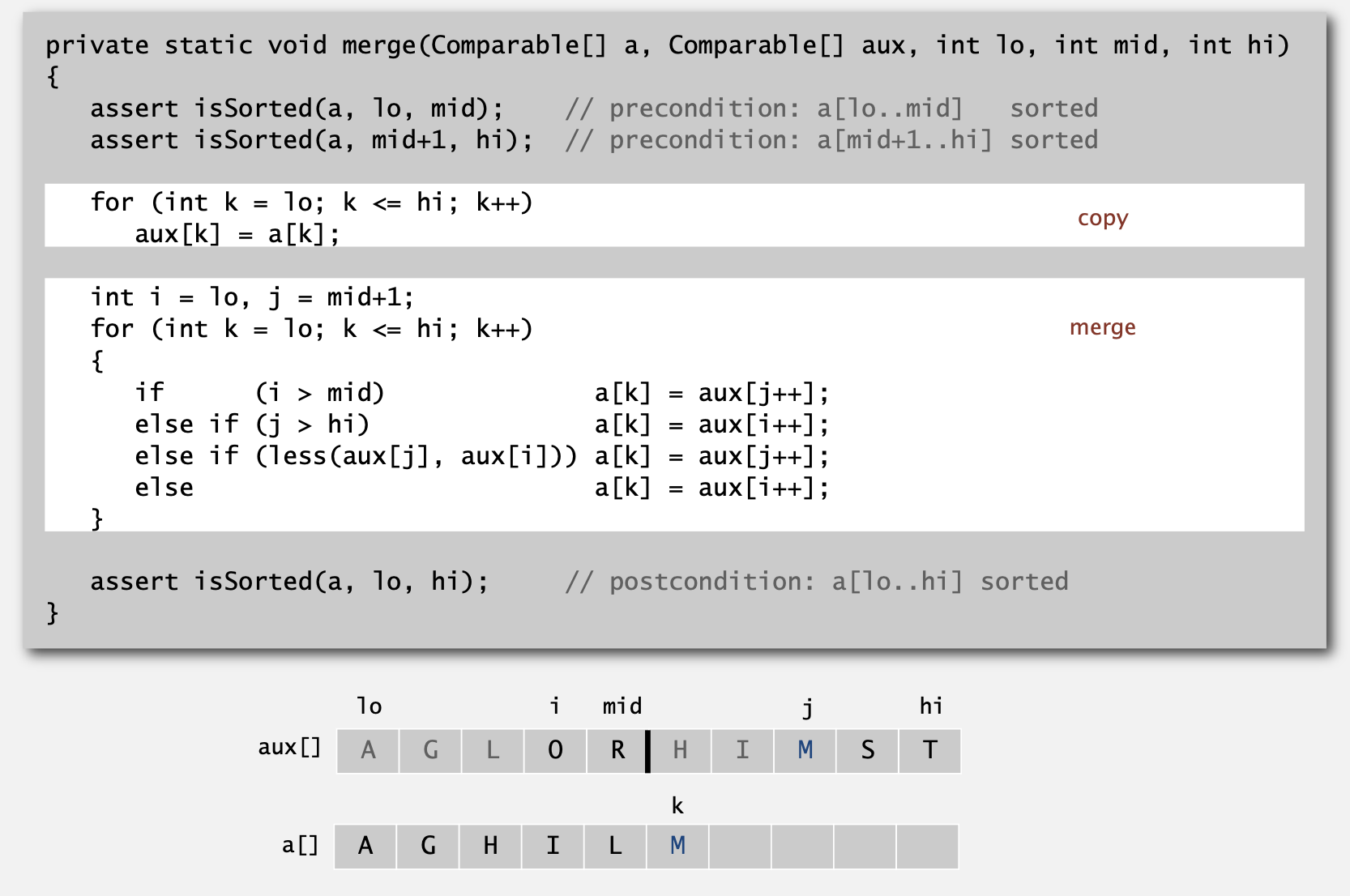
def merge(a, aux, lo, mid, hi):
assert isSorted(a, lo, mid)
assert isSorted(a, mid+1, hi)
for k in range(lo, hi+1):
aux[k] = a[k]
i, j = lo, mid+1
for k in range(lo, hi+1):
if i > mid:
a[k] = aux[j]
j += 1
elif j > hi:
a[k] = aux[i]
i += 1
elif aux[j] < aux[i]:
a[k] = aux[j]
j += 1
else:
a[k] = aux[i]
i += 1
assert isSorted(a, lo, hi)- 파이썬 코드로 변환하면 위와 같습니다.
조건문을 보면 범위가 벗어난 경우를 먼저 처리하고, 범위 내의 경우 대소를 비교하여 k번째 값을 업데이트 하는 것을 알 수 있습니다.
Assertions

- assertion 코드를 사용하여 입력에 문제가 없는지 살펴볼 수 있었습니다.
이는 코드상에 문제가 있는지 없는지를 사전에 확인해주는 기능을 갖고 있습니다.
Mergesort: Java implementation
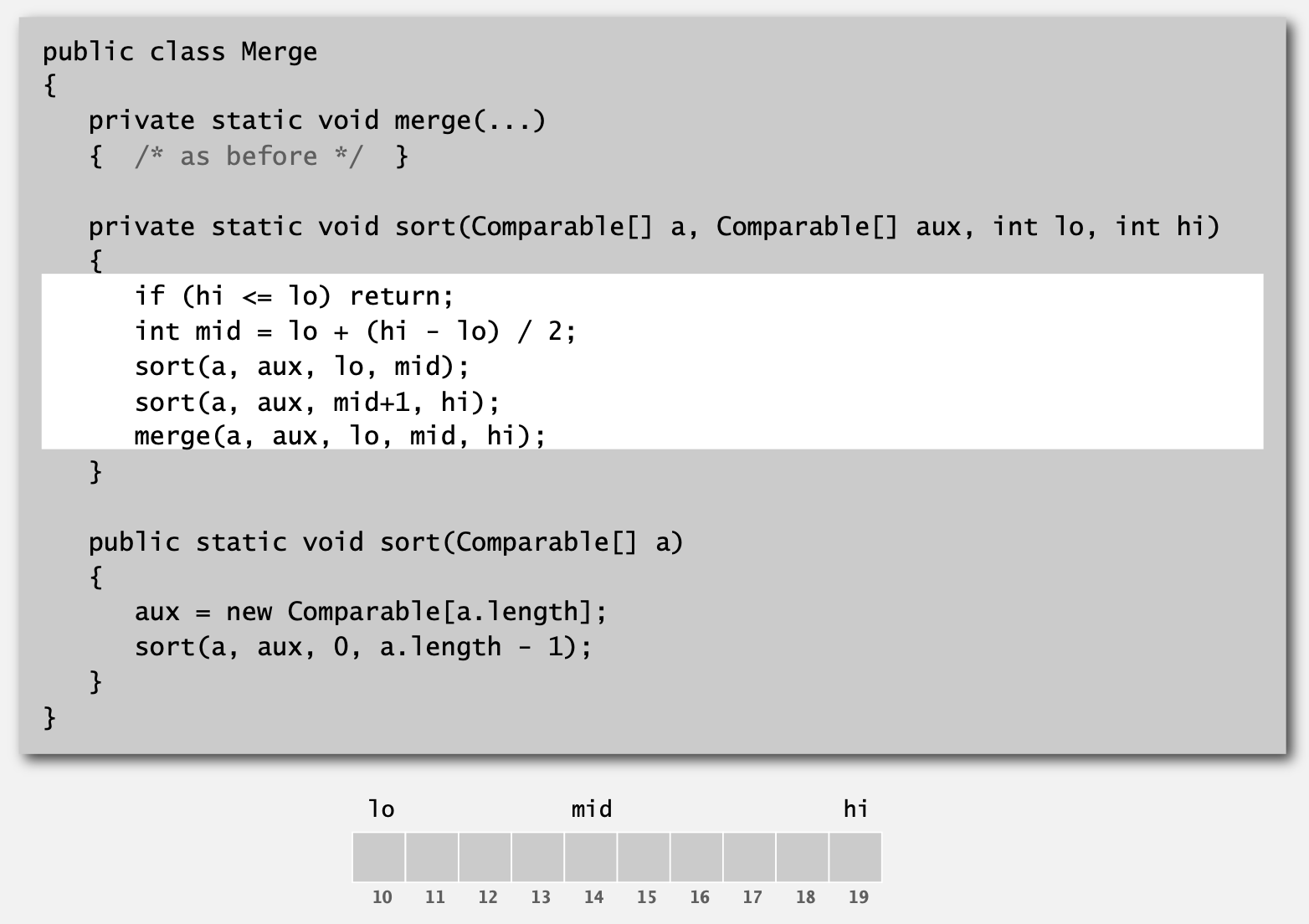
def sort(a, aux, lo, hi):
if hi <= lo:
return
mid = lo + (hi-lo) // 2
sort(a, aux, lo, mid)
sort(a, aux, mid+1, hi)
merge(a, aux, lo, mid, hi)- sort 함수에서는 lo, mid, hi 값을 조정하면서 분할을 수행합니다.
이를 위에서 정의한 merge 함수와 결합하여 '분할 정복(divide & conquer)' 알고리즘을 구현한 것을 알 수 있습니다.
Mergesort: trace

Mergesort: impirical analysis

- 병합 정렬은 삽입 정렬에 비해 어마무시하게 효율적인 알고리즘이라는 것을 위 표를 통해 알 수 있습니다.
이 강의의 메인 주제 중 하나는 시간, 자원을 낭비하는 것보다 효율적인 알고리즘을 이용하는 것의 중요성이라고 다시 강조합니다.
Mergesort: number of compares and array accesses

- C(compare)는 비교, A(array)는 배열에 접근하는 횟수를 뜻합니다.
N이 2의 제곱인 경우를 가정해보면 위 식을 증명하기 쉽습니다.
Divide-and-conquer recurrence: proof by picture
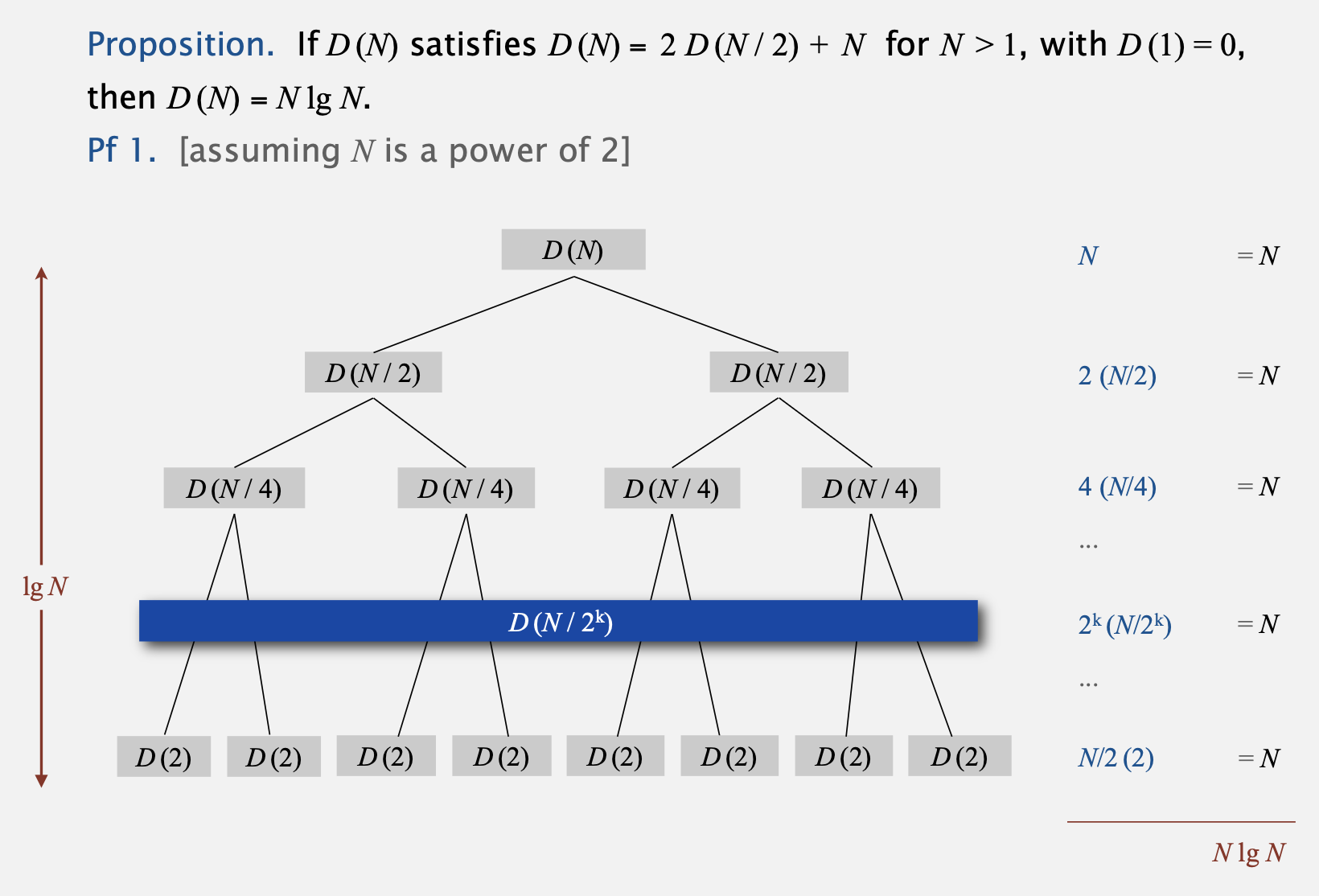

- 주어진 배열을 2로 나누었을 때, 분할된 각 배열에 대해 병합을 수행하는 것은 N만큼의 시간이 걸립니다.
- 하지만 주어진 배열을 2로 쪼개다보면 이는 logN만큼의 step이 됩니다.
이를 각 step에 걸리는 시간과 곱하면 NlogN이 되는 것을 알 수 있습니다. - 우측의 식은 N을 계속해서 쪼개며 logN의 시간이 소요됨을 식으로 증명하고 있습니다.
Divide-and-conquer recurrence: proof by induction

- 물론 이렇게 가설을 검증하는 방식으로도 증명이 가능합니다.
Mergesort analysis: memory
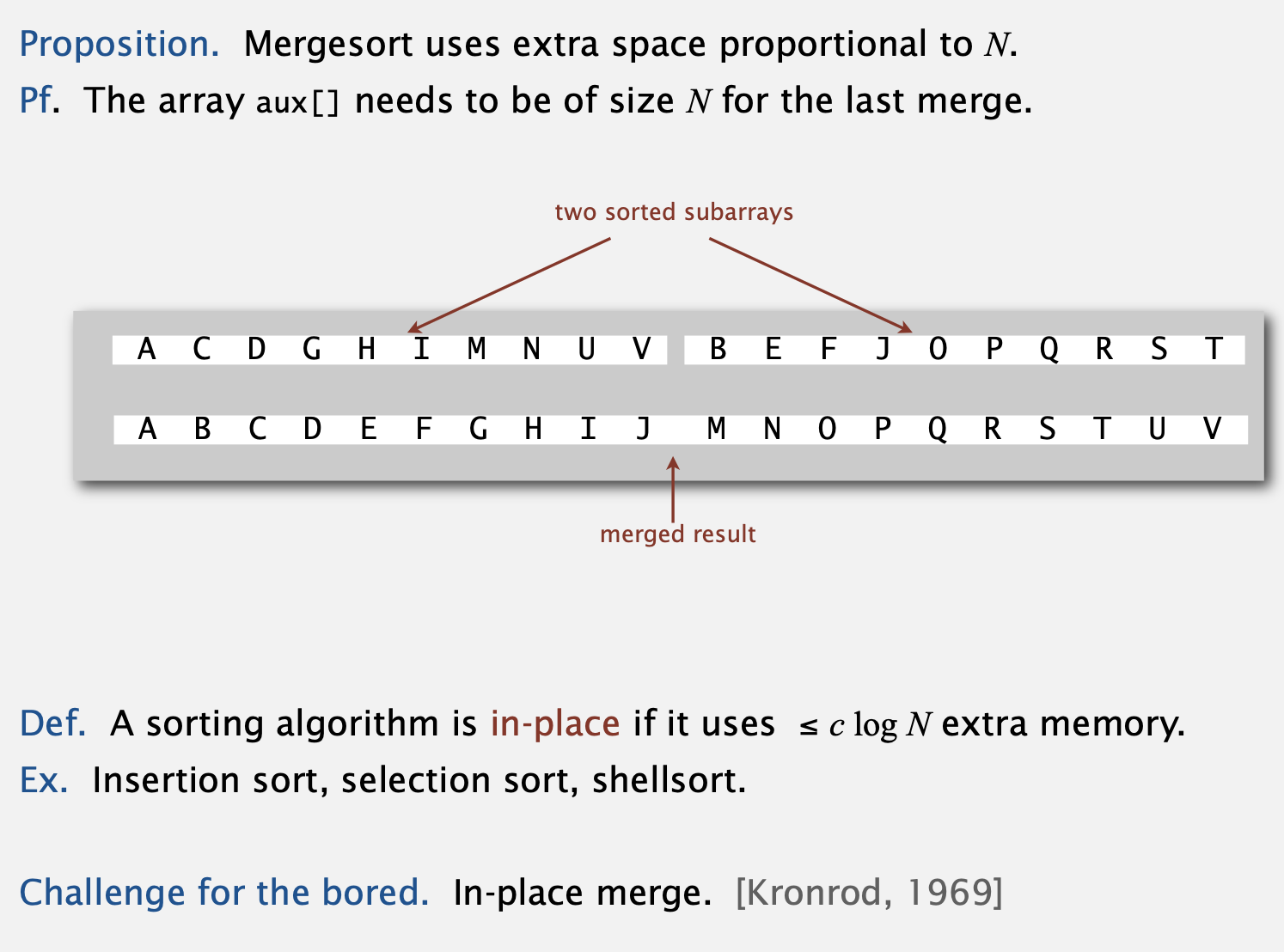
- 병합 정렬은 기존의 배열과 동일한 aux 배열을 갖게 되므로 메모리가 추가로 필요합니다.
Mergesort: practical improvements
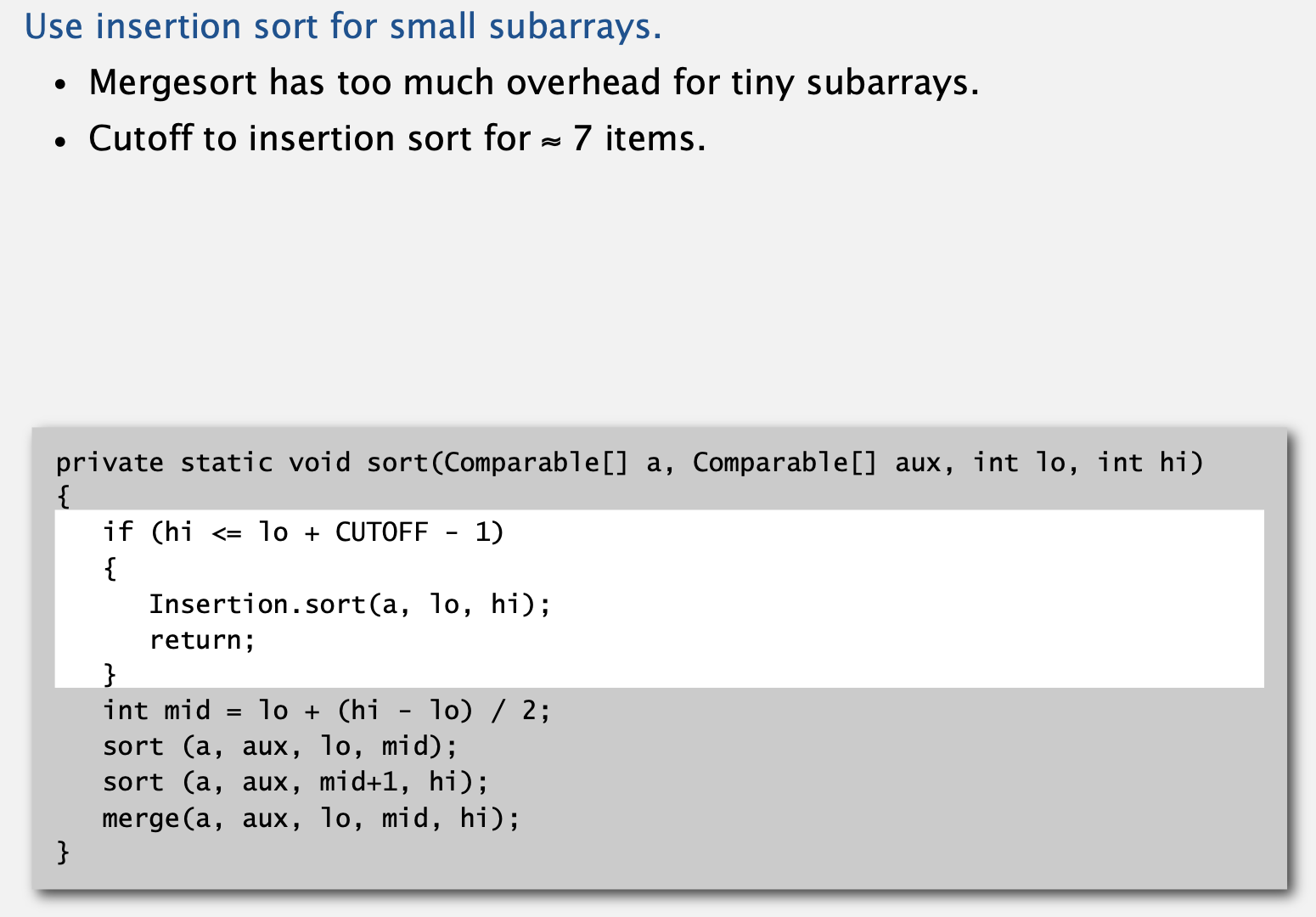

- 병합 정렬을 개선할 수 있는 방법은 여러 가지가 존재합니다.
- 병합 정렬은 너무 작은 배열에 대해 부적합하므로, 삽입 정렬을 추가하여 이를 개선할 수 있습니다.
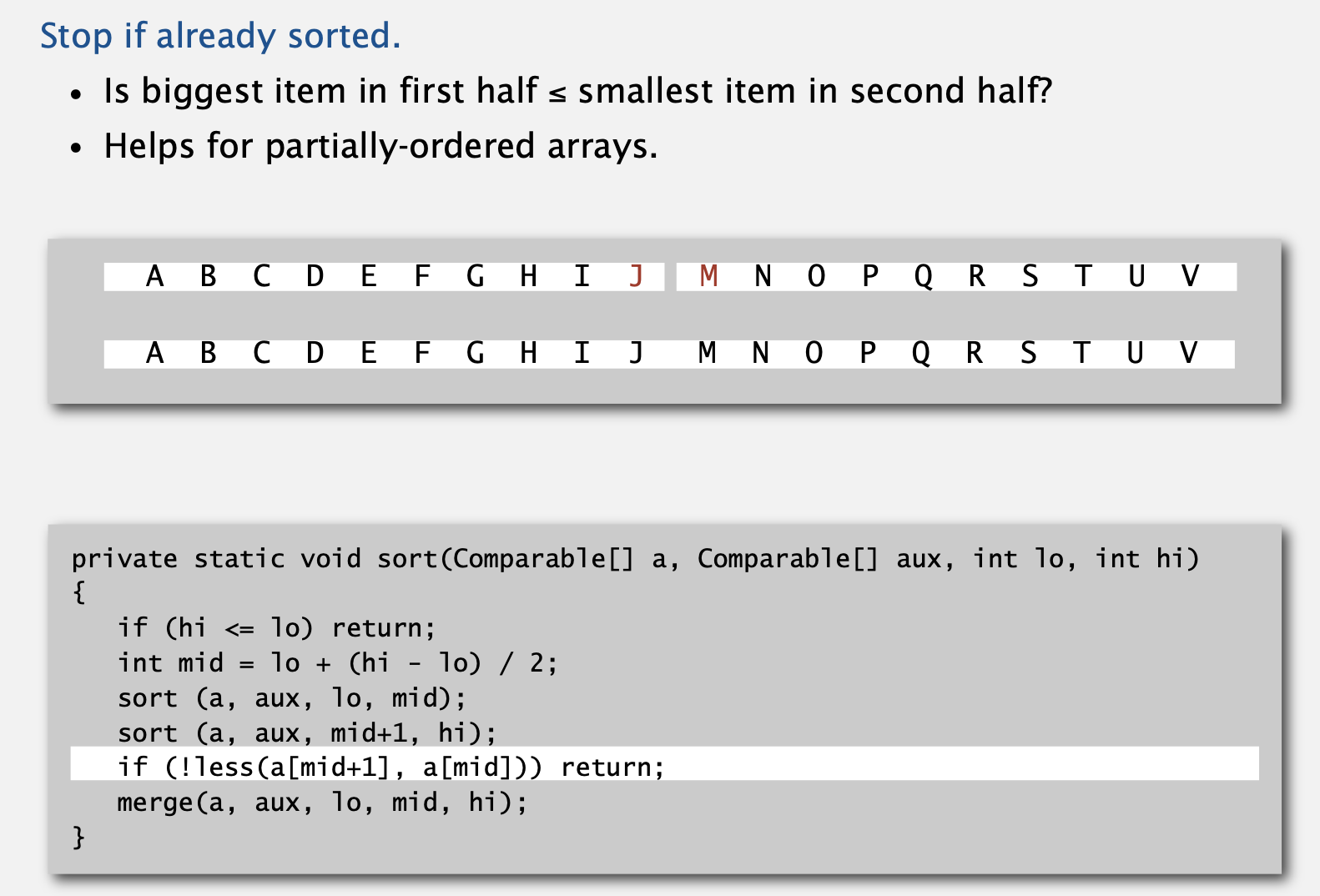
- 부분적으로 정렬된 배열에 대해 break(return)를 걸어줌으로써 알고리즘을 개선할 수 있습니다.
- 재귀적으로 함수를 호출하는 과정에서, 오리지날 배열과 aux 배열의 역할을 교환하여 시간을 아낄 수 있습니다.
Bottom-up mergesort

- 중간부터 절반씩 쪼개는 것이 아니라, 1부터 시작하여 2를 곱하는 범위 내의 부분 정렬을 합치는 방식으로 정렬을 구현한 것이 bottom-up 방식입니다.
- 범위가 2를 곱하는 방식으로 증가하기 때문에 logN 만큼의 step이 존재하고, 각 step에서 N만큼의 배열 접근이 발생하기 때문에 총 시간 복잡도는 NlogN으로 일반 병합 정렬과 동일합니다.
Bottom-up mergesort: Java implementation
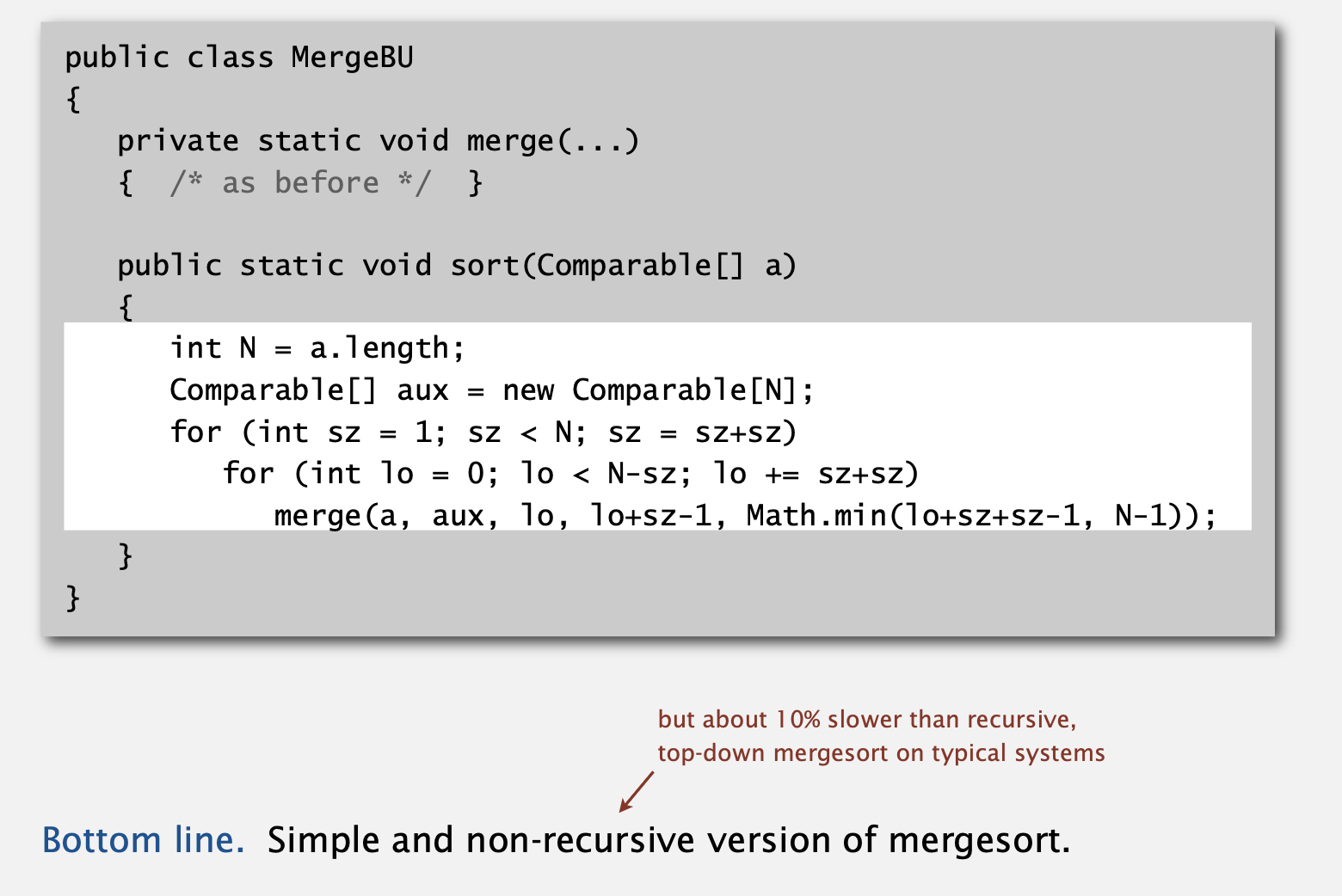
def MergeBU(a):
n = len(a)
aux = []
for sz in range(1,n,sz):
for lo in range(0,n-sz,sz):
merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, n-1))- 사용된 merge 함수는 위와 동일합니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 3주차' 카테고리의 다른 글
| Quicksort(3) : Duplicate Keys (0) | 2023.04.25 |
|---|---|
| Quicksort(2) : Selection (0) | 2023.04.21 |
| Quicksort(1) : Quicksort (0) | 2023.04.21 |
| Mergesort(4),(5) : comparators, stability (0) | 2023.04.20 |
| Mergesort(3) : Sorting Complexity (0) | 2023.04.20 |
