Complexity of sorting

- 정렬 알고리즘의 계산 복잡도를 정리하는 내용입니다.
상한선은 당연히 최대치/최악의 경우를 나타내고 있으므로 guarantee라는 표현이 쓰였습니다. - 하한선은 이보다 더 좋을 수 없는 최선의 경우가 증명된 것을 뜻합니다.
- 최적 알고리즘은 X라는 문제에 대해 최선의 것으로 증명된 경우에 해당하며 상한선과 하한선 사이에 위치합니다.
Decision tree (for 3 distinct a, b, and c)
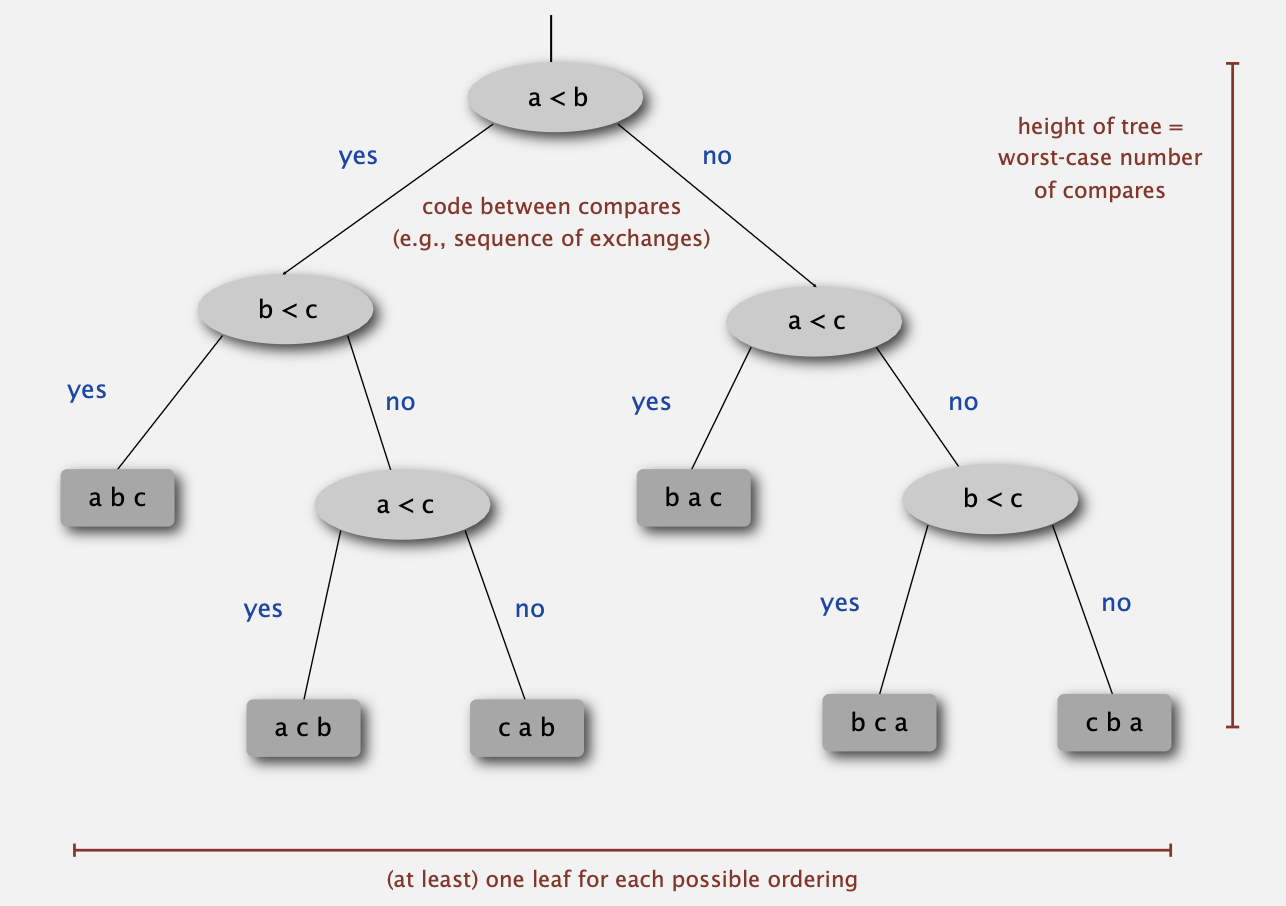
- 의사 결정 나무를 통해 정렬에 대한 결정을 시각화할 수 있습니다.
여기서는 각 비교를 합쳐 맨 마지막에 세 개의 값을 비교한 결과물을 얻어낼 수 있음을 보여주고 있습니다. - 트리의 높이는 비교를 가장 많이 해야 하는 최악의 경우를 뜻하게 됩니다.
Compare-based lower bound for sorting


- 의사 결정 나무를 통해 정렬 알고리즘의 상한선과 하한선을 증명하고 있습니다.
- 최악의 경우에 해당하는 트리의 높이 h에 대해, 이진 트리는 2의 h승만큼의 leaves를 갖습니다.
- 또 N개의 값에 대해 정렬하는 상황에서는 적어도 N!의 leaves가 존재할 것을 알 수 있습니다.
- 따라서 leaves의 개수는 2^h 보다는 적고 N! 보다는 많다고 부등식이 정리됩니다.
- 여기에 log를 취하면 log(N!)이 NlogN에 비례하기 때문에 하한선이 NlogN이 되는 것을 알 수 있습니다.
Complexity of sorting

- 따라서 상한선과 하한선에 mergesort(합병 정렬)을 기준으로 설정됩니다.
Complexity results in context


- 하지만 이전에 살펴본 것처럼 합병 정렬은 메모리 관리 측면에서는 효율적이지 않습니다.
오리지날 배열을 복사한 aux 배열을 활용하기 때문에 적어도 두 배 이상의 메모리를 차지하게 되기 때문이죠. - 또한 복잡도에 관한 재밌는 특징 중 하나는 하한선에 그다지 많은 정보가 포함되어 있지 않다는 것입니다.
- 왜냐하면 하한선은 최선의 경우를 가정하고 구한 복잡도인데, 사실 key values의 분포나, key의 특징, 정렬된 상태에 따라 이것에 영향을 줄 수 있는 요소가 너무 많기 때문이죠.
- 아마 이런 점 때문에 우리가 일반적으로 시간 복잡도를 계산할 때는 최악을 가정하는 빅 오 표기법을 쓰는게 아닐까 싶었습니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 3주차' 카테고리의 다른 글
| Quicksort(3) : Duplicate Keys (0) | 2023.04.25 |
|---|---|
| Quicksort(2) : Selection (0) | 2023.04.21 |
| Quicksort(1) : Quicksort (0) | 2023.04.21 |
| Mergesort(4),(5) : comparators, stability (0) | 2023.04.20 |
| Mergesort(1),(2) : Mergesort, Bottom-up Mergesort (0) | 2023.04.19 |
Complexity of sorting

- 정렬 알고리즘의 계산 복잡도를 정리하는 내용입니다.
상한선은 당연히 최대치/최악의 경우를 나타내고 있으므로 guarantee라는 표현이 쓰였습니다. - 하한선은 이보다 더 좋을 수 없는 최선의 경우가 증명된 것을 뜻합니다.
- 최적 알고리즘은 X라는 문제에 대해 최선의 것으로 증명된 경우에 해당하며 상한선과 하한선 사이에 위치합니다.
Decision tree (for 3 distinct a, b, and c)

- 의사 결정 나무를 통해 정렬에 대한 결정을 시각화할 수 있습니다.
여기서는 각 비교를 합쳐 맨 마지막에 세 개의 값을 비교한 결과물을 얻어낼 수 있음을 보여주고 있습니다. - 트리의 높이는 비교를 가장 많이 해야 하는 최악의 경우를 뜻하게 됩니다.
Compare-based lower bound for sorting


- 의사 결정 나무를 통해 정렬 알고리즘의 상한선과 하한선을 증명하고 있습니다.
- 최악의 경우에 해당하는 트리의 높이 h에 대해, 이진 트리는 2의 h승만큼의 leaves를 갖습니다.
- 또 N개의 값에 대해 정렬하는 상황에서는 적어도 N!의 leaves가 존재할 것을 알 수 있습니다.
- 따라서 leaves의 개수는 2^h 보다는 적고 N! 보다는 많다고 부등식이 정리됩니다.
- 여기에 log를 취하면 log(N!)이 NlogN에 비례하기 때문에 하한선이 NlogN이 되는 것을 알 수 있습니다.
Complexity of sorting

- 따라서 상한선과 하한선에 mergesort(합병 정렬)을 기준으로 설정됩니다.
Complexity results in context


- 하지만 이전에 살펴본 것처럼 합병 정렬은 메모리 관리 측면에서는 효율적이지 않습니다.
오리지날 배열을 복사한 aux 배열을 활용하기 때문에 적어도 두 배 이상의 메모리를 차지하게 되기 때문이죠. - 또한 복잡도에 관한 재밌는 특징 중 하나는 하한선에 그다지 많은 정보가 포함되어 있지 않다는 것입니다.
- 왜냐하면 하한선은 최선의 경우를 가정하고 구한 복잡도인데, 사실 key values의 분포나, key의 특징, 정렬된 상태에 따라 이것에 영향을 줄 수 있는 요소가 너무 많기 때문이죠.
- 아마 이런 점 때문에 우리가 일반적으로 시간 복잡도를 계산할 때는 최악을 가정하는 빅 오 표기법을 쓰는게 아닐까 싶었습니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 3주차' 카테고리의 다른 글
| Quicksort(3) : Duplicate Keys (0) | 2023.04.25 |
|---|---|
| Quicksort(2) : Selection (0) | 2023.04.21 |
| Quicksort(1) : Quicksort (0) | 2023.04.21 |
| Mergesort(4),(5) : comparators, stability (0) | 2023.04.20 |
| Mergesort(1),(2) : Mergesort, Bottom-up Mergesort (0) | 2023.04.19 |
