1. Determinants and inverses
Determinant
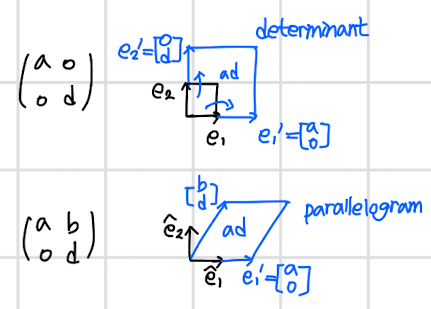
- 공간이 얼마나 넓어졌는지를 나타내는 지표
- 2차원 기준 평행사다리꼴의 면적이 위 예시에 동일하다는 것을 확인할 수 있다. 즉, 행렬식이 같은 경우다.
2차원의 행렬식 구하기

- 2차원의 행렬식은 ad-bc 가 된다.
- 역행렬과 1 / 행렬식, 행렬을 곱하면 단위 행렬이 된다.
행렬식과 역행렬의 관계

- 행렬식이 0인 경우 역행렬은 존재하지 않는다.
- 행렬식이 0이라는 것은 어떤 문제를 풀기에 정보가 불충분하다는 것을 의미하기 때문이다.
- 따라서 기약행 사다리꼴을 만들었을 때, 각 열벡터가 선형 독립이어야만 필요한 정보를 모두 갖추고 있는 것으로 이해할 수 있다.
여기서 선형 독립은, 어떤 열벡터를 다른 열벡터들의 연산을 통해 얻지 못한다는 것을 의미한다.
2. Identifying special matrices
주피터 노트북에서 기약행 사다리꼴 행렬을 만드는 코드 작성하기
- 어떻게 뭘 채우라는건지 알아보기 어렵다.
- 구글링하면 정답 코드도 존재하는 것 같다.
- 풀이를 제출하면 알아서 채점해준다.
출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
'Linear Algebra > 3주차' 카테고리의 다른 글
| Matrix Inverses (0) | 2022.09.17 |
|---|---|
| Matrices in linear algebra: operating on vectors (0) | 2022.09.17 |
1. Determinants and inverses
Determinant

- 공간이 얼마나 넓어졌는지를 나타내는 지표
- 2차원 기준 평행사다리꼴의 면적이 위 예시에 동일하다는 것을 확인할 수 있다. 즉, 행렬식이 같은 경우다.
2차원의 행렬식 구하기

- 2차원의 행렬식은 ad-bc 가 된다.
- 역행렬과 1 / 행렬식, 행렬을 곱하면 단위 행렬이 된다.
행렬식과 역행렬의 관계

- 행렬식이 0인 경우 역행렬은 존재하지 않는다.
- 행렬식이 0이라는 것은 어떤 문제를 풀기에 정보가 불충분하다는 것을 의미하기 때문이다.
- 따라서 기약행 사다리꼴을 만들었을 때, 각 열벡터가 선형 독립이어야만 필요한 정보를 모두 갖추고 있는 것으로 이해할 수 있다.
여기서 선형 독립은, 어떤 열벡터를 다른 열벡터들의 연산을 통해 얻지 못한다는 것을 의미한다.
2. Identifying special matrices
주피터 노트북에서 기약행 사다리꼴 행렬을 만드는 코드 작성하기
- 어떻게 뭘 채우라는건지 알아보기 어렵다.
- 구글링하면 정답 코드도 존재하는 것 같다.
- 풀이를 제출하면 알아서 채점해준다.
출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
'Linear Algebra > 3주차' 카테고리의 다른 글
| Matrix Inverses (0) | 2022.09.17 |
|---|---|
| Matrices in linear algebra: operating on vectors (0) | 2022.09.17 |
