목차
1. Changing to the eigenbasis
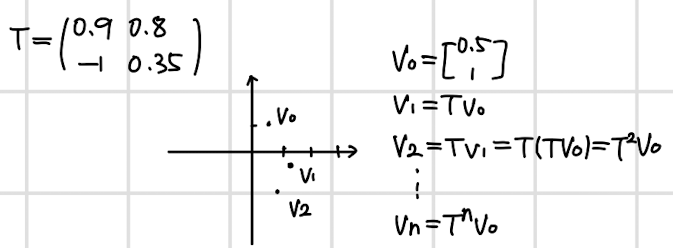
- T라는 사상이 주어진 벡터를 어떻게 이동시키는지는 매번 행렬 T를 곱해보아야 알 수 있다.
- 그러나 시행 횟수 n이 커질수록 이 계산은 매우 복잡해지므로 간단하게 만들고자 한다.
- 이때 diagonal matrix(대각행렬)를 사용하면 이 과정을 간단하게 만들 수 있다.
대각행렬은 주대각선은 전부 1이고, 나머지는 전부 0인 행렬을 말한다.
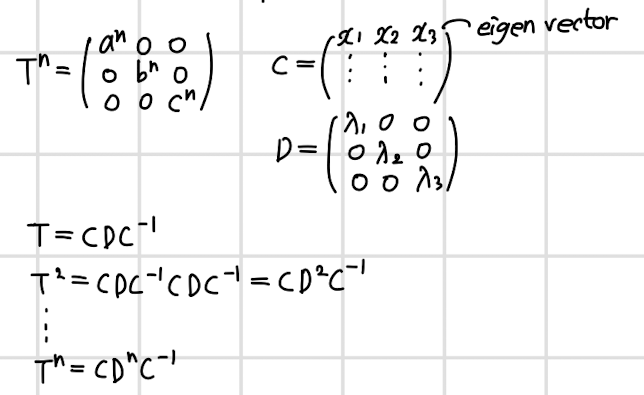
- 대각행렬 T를 반복적으로 곱하면 주대각성분만 제곱의 형태가 된다.
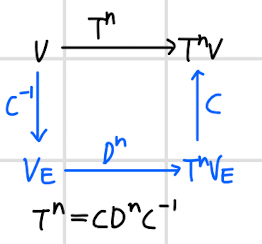
- 고유벡터로 이루어진 행렬 C와, 단위 행렬에 고윳값을 곱한 행렬 D가 있다.
- T를 위와 같은 방식으로 구하면 C와 C의 역행렬이 사라지며 계산량이 확연하게 줄어들고 일반화도 가능하다.
2. Eigenbasis example
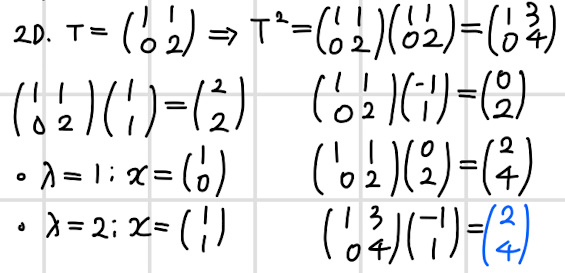
- horizontal shear 사상을 가진 행렬 T의 고유벡터와 고윳값을 구한다.
- 여기서 구한 고유벡터에 좌표를 곱해주면 T 사상을 기준으로 좌표가 표현된다.
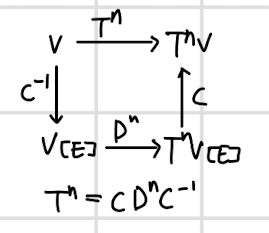
- 이제는 T의 n승을 그대로 구해 계산하지 않고 고유벡터와 그 역행렬을 통해 구해보고자 한다.
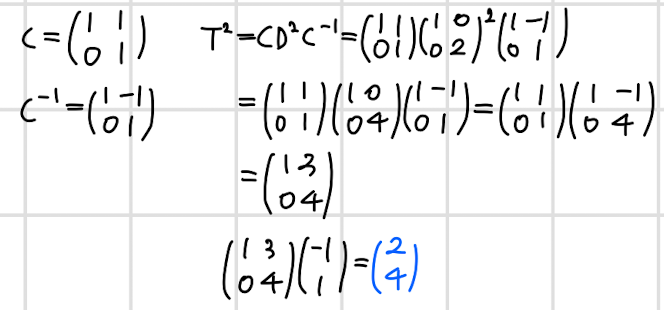
- 동일한 결과가 나온다는 것을 알 수 있다.
- 반복 횟수가 커질수록 실제 계산해야 되는 양이 줄어드므로 이 방식이 훨씬 효율적이다.
- 중간에 계산되는 행렬 D가 대각행렬이기 때문에 연산이 아주 간편하다.
- 이 개념은 다차원으로 혹은 직사각행렬으로 확장될 수 있다.
3. Diagonalisation(대각선화) and applications
- 2차원 벡터 T를 기준으로 D를 구하거나 혹은 그 반대를 구하는 문제 (4문항)
- 2차원 벡터 T의 n승을 구하는 문제(eigen vector 활용) (3문항)
4. Visualising Matrices and Eigen
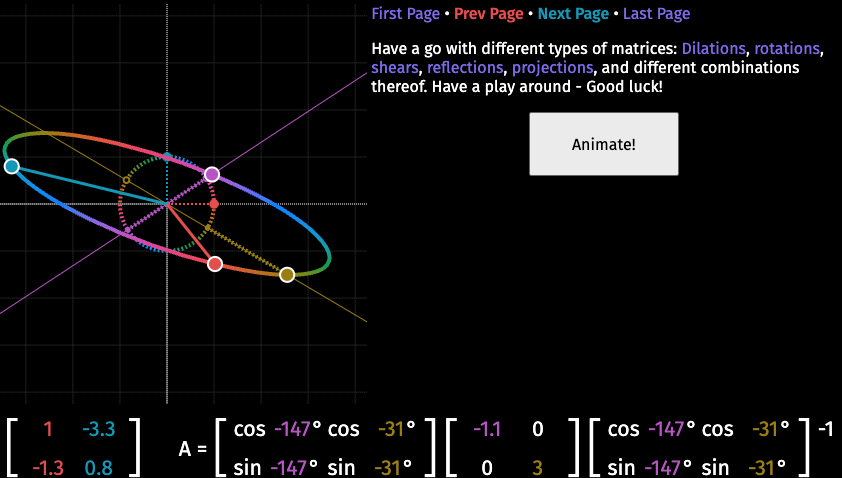
- 팽창, 회전, 기울기, 반사 등의 변형을 직접 시각적으로 확인할 수 있는 툴
출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
'Linear Algebra > 5주차' 카테고리의 다른 글
| Eigenvalues and eigenvectors: Assessment (0) | 2022.09.20 |
|---|---|
| Making the PageRank algorithm (0) | 2022.09.19 |
| Getting into the detail of eigenproblems (0) | 2022.09.18 |
| What are eigen-things? (0) | 2022.09.18 |
1. Changing to the eigenbasis

- T라는 사상이 주어진 벡터를 어떻게 이동시키는지는 매번 행렬 T를 곱해보아야 알 수 있다.
- 그러나 시행 횟수 n이 커질수록 이 계산은 매우 복잡해지므로 간단하게 만들고자 한다.
- 이때 diagonal matrix(대각행렬)를 사용하면 이 과정을 간단하게 만들 수 있다.
대각행렬은 주대각선은 전부 1이고, 나머지는 전부 0인 행렬을 말한다.
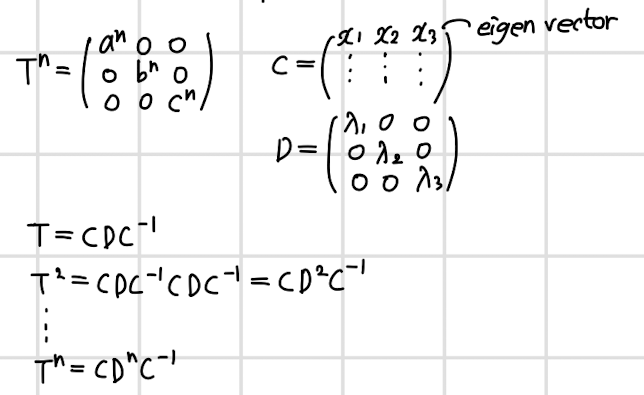
- 대각행렬 T를 반복적으로 곱하면 주대각성분만 제곱의 형태가 된다.
- 고유벡터로 이루어진 행렬 C와, 단위 행렬에 고윳값을 곱한 행렬 D가 있다.
- T를 위와 같은 방식으로 구하면 C와 C의 역행렬이 사라지며 계산량이 확연하게 줄어들고 일반화도 가능하다.

2. Eigenbasis example
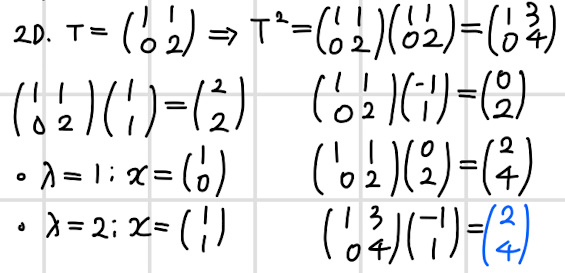
- horizontal shear 사상을 가진 행렬 T의 고유벡터와 고윳값을 구한다.
- 여기서 구한 고유벡터에 좌표를 곱해주면 T 사상을 기준으로 좌표가 표현된다.

- 이제는 T의 n승을 그대로 구해 계산하지 않고 고유벡터와 그 역행렬을 통해 구해보고자 한다.
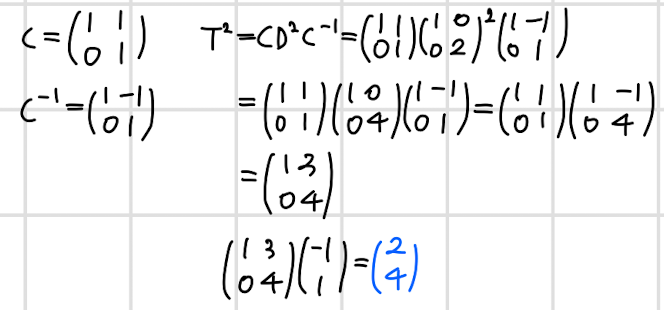
- 동일한 결과가 나온다는 것을 알 수 있다.
- 반복 횟수가 커질수록 실제 계산해야 되는 양이 줄어드므로 이 방식이 훨씬 효율적이다.
- 중간에 계산되는 행렬 D가 대각행렬이기 때문에 연산이 아주 간편하다.
- 이 개념은 다차원으로 혹은 직사각행렬으로 확장될 수 있다.
3. Diagonalisation(대각선화) and applications
- 2차원 벡터 T를 기준으로 D를 구하거나 혹은 그 반대를 구하는 문제 (4문항)
- 2차원 벡터 T의 n승을 구하는 문제(eigen vector 활용) (3문항)
4. Visualising Matrices and Eigen

- 팽창, 회전, 기울기, 반사 등의 변형을 직접 시각적으로 확인할 수 있는 툴
출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
'Linear Algebra > 5주차' 카테고리의 다른 글
| Eigenvalues and eigenvectors: Assessment (0) | 2022.09.20 |
|---|---|
| Making the PageRank algorithm (0) | 2022.09.19 |
| Getting into the detail of eigenproblems (0) | 2022.09.18 |
| What are eigen-things? (0) | 2022.09.18 |
