목차
1. Rise Over Run( rise: y축 증가량, run: x축 증가량)
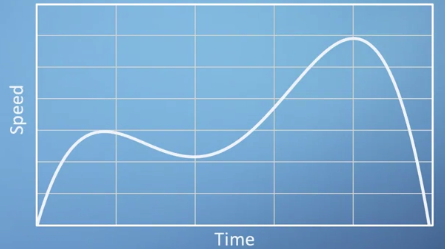
- horizontal line(수평선)은 속도가 동일함을 의미한다.
- accleration: local gradient of a speed-time graph, function of time in graph
- deceleration: negative slope
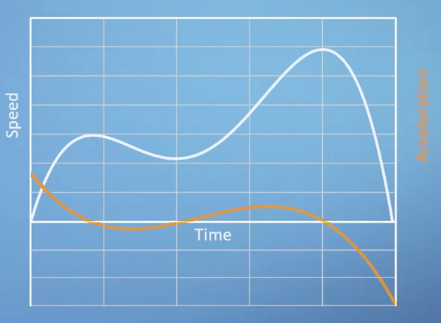
- 시간에 따른 가속도 그래프는 위와 같다.
- 각 지점에서의 경사(slope)를 나타내고 있다.
- 노란색 그래프가 양수인 지점은 속도가 증가하고 있음을, 음수인 지점은 속도가 감소하고 있음을 나타낸다.
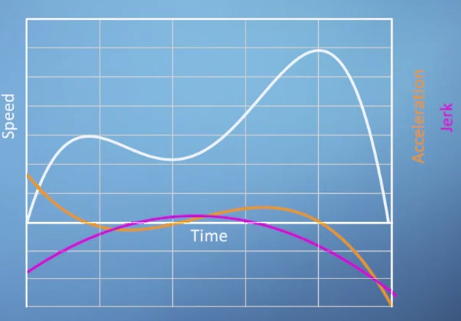
- 가속도 그래프를 한 번 더 미분한 그래프는 보라색으로 표현된다.
- 이것은 차의 흔들거림(jerk)를 나타내게 된다.
- 이런 과정을 거꾸로 하는 것이 anti-derivative라고 불리고 integral과 관련이 있다.
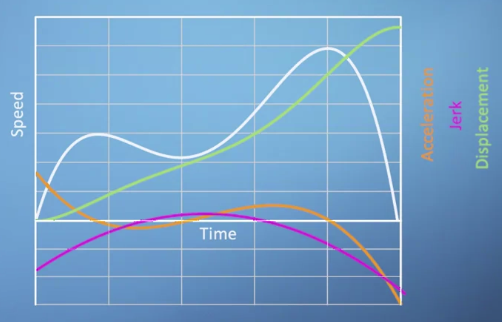
- 시간에 따른 출발점으로부터의 자동차 거리를 나타낸 것이 초록색 선이다.
2. Matching the graph of a function to the graph of its derivative
- 주어진 함수를 보고 알맞은 도함수를 고르는 문제 4개(미분)
- 주어진 도함수를 보고 알맞은 원함수를 모두 고르는 문제 1개(적분)
- 직접 계산하는 스타일은 아니고 직관적으로 미분과 적분의 개념을 파악하는 문제들같다.
고등학교 교육과정에서 미적분을 배우지 않았더라면 이정도의 설명만으로 간단히 풀 수 있었을지는 잘 모르겠다
3. Definition of a derivative
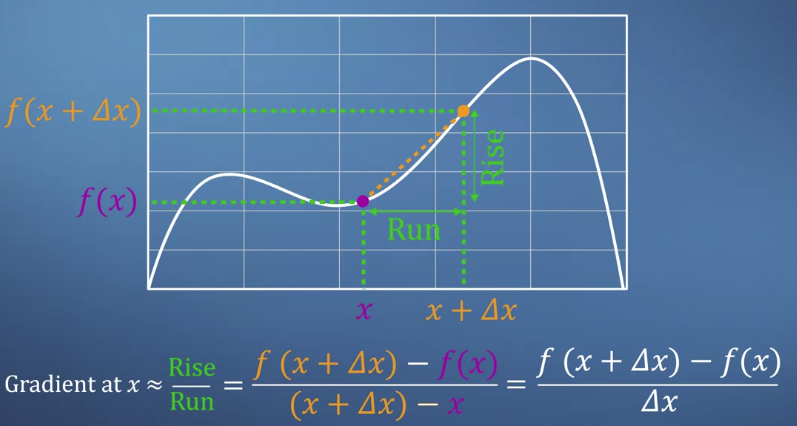
- x에서의 gradient는 위와같이 정의된다.
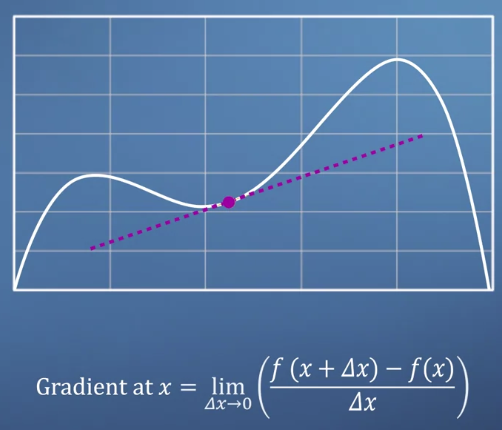
- 델타 x가 0이라는 것을 의미하지 않는다. 0으로 나누는 것은 정의될 수 없기 때문이다.
- 델타 x를 0에 extremely 가깝게 만드는 것이고, 이를 extreme rise over run이라고 부른다.
- 이를 df/dx 또는 f'(x) 라고 표현할 수도 있다.
- 이러한 과정을 differentiate(미분하다)라고 한다.
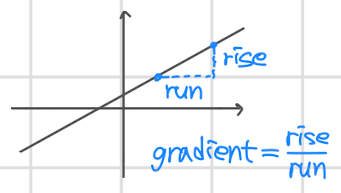
- gradient(기울기)는 위와 같이 'y축의 변화량 / x축의 변화량' 으로 표현된다.
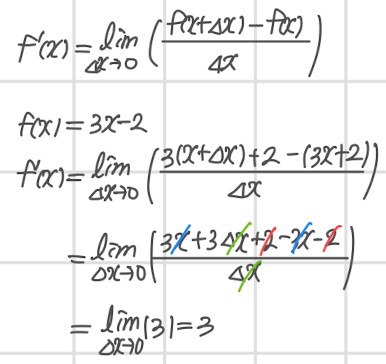
- 미분의 정의에 따라 f(x) = 3x - 2 를 미분한 식과 결과는 위와 같다.

- 미분에 대해서는 위 두가지 rule이 적용된다.
다항수 미분에 대한 결과를 간략하게 표현할 수 있는 Power Rule(b는 정수가 아니어도 된다),
두 함수를 미분한 것을 합친 것은 두 함수를 합쳐서 미분한 것과 동일하다는 Sum Rule이다.
4. Differentiation examples & speicial cases
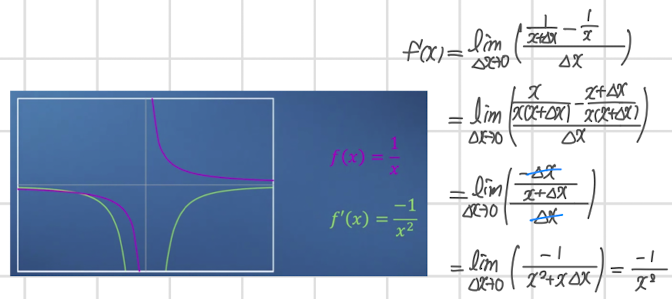
4.1. f(x) = 1 / x
4.2. 지수함수
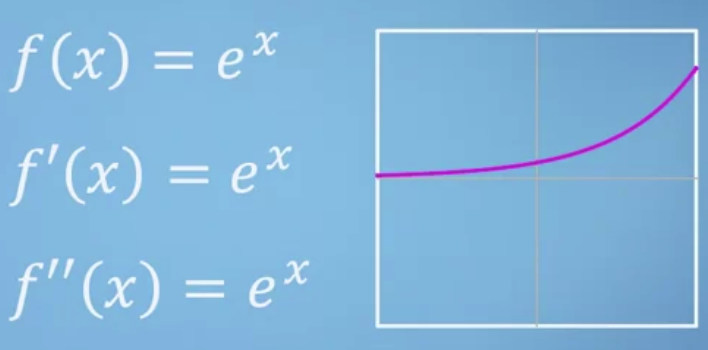
- exponential 함수는 미분을 하면 그 결과로 자기 자신이 나온다.
4.3. Trigonometric Functions, Sine and Cosine(삼각함수)

- sin을 미분하면 cos이다.
- cos을 미분하면 -sin이다.
- -sin을 미분하면 -cos이다.
- -cos을 미분하면 다시 sin으로 돌아온다.
즉 네 번을 주기로 미분의 결과가 반복된다는 것을 알 수 있다.
5. Let's differentiate some functions
- 다항함수 미분(1문제)
- 분수함수 미분(1문제)
- 지수함수 + 삼각함수 미분(1문제)
- 정적분(1문제)
- 무리함수 미분(1문제)
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 1주차' 카테고리의 다른 글
| Time saving rules (2) | 2022.09.24 |
|---|---|
| Back to basics: functions (1) | 2022.09.23 |
1. Rise Over Run( rise: y축 증가량, run: x축 증가량)

- horizontal line(수평선)은 속도가 동일함을 의미한다.
- accleration: local gradient of a speed-time graph, function of time in graph
- deceleration: negative slope

- 시간에 따른 가속도 그래프는 위와 같다.
- 각 지점에서의 경사(slope)를 나타내고 있다.
- 노란색 그래프가 양수인 지점은 속도가 증가하고 있음을, 음수인 지점은 속도가 감소하고 있음을 나타낸다.

- 가속도 그래프를 한 번 더 미분한 그래프는 보라색으로 표현된다.
- 이것은 차의 흔들거림(jerk)를 나타내게 된다.
- 이런 과정을 거꾸로 하는 것이 anti-derivative라고 불리고 integral과 관련이 있다.

- 시간에 따른 출발점으로부터의 자동차 거리를 나타낸 것이 초록색 선이다.
2. Matching the graph of a function to the graph of its derivative
- 주어진 함수를 보고 알맞은 도함수를 고르는 문제 4개(미분)
- 주어진 도함수를 보고 알맞은 원함수를 모두 고르는 문제 1개(적분)
- 직접 계산하는 스타일은 아니고 직관적으로 미분과 적분의 개념을 파악하는 문제들같다.
고등학교 교육과정에서 미적분을 배우지 않았더라면 이정도의 설명만으로 간단히 풀 수 있었을지는 잘 모르겠다
3. Definition of a derivative

- x에서의 gradient는 위와같이 정의된다.

- 델타 x가 0이라는 것을 의미하지 않는다. 0으로 나누는 것은 정의될 수 없기 때문이다.
- 델타 x를 0에 extremely 가깝게 만드는 것이고, 이를 extreme rise over run이라고 부른다.
- 이를 df/dx 또는 f'(x) 라고 표현할 수도 있다.
- 이러한 과정을 differentiate(미분하다)라고 한다.

- gradient(기울기)는 위와 같이 'y축의 변화량 / x축의 변화량' 으로 표현된다.
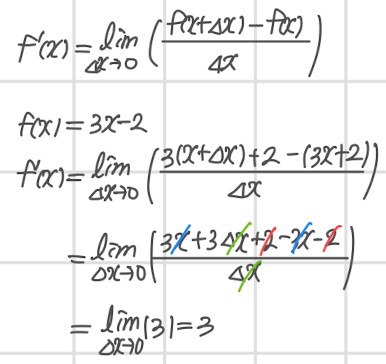
- 미분의 정의에 따라 f(x) = 3x - 2 를 미분한 식과 결과는 위와 같다.

- 미분에 대해서는 위 두가지 rule이 적용된다.
다항수 미분에 대한 결과를 간략하게 표현할 수 있는 Power Rule(b는 정수가 아니어도 된다),
두 함수를 미분한 것을 합친 것은 두 함수를 합쳐서 미분한 것과 동일하다는 Sum Rule이다.
4. Differentiation examples & speicial cases
4.1. f(x) = 1 / x

4.2. 지수함수

- exponential 함수는 미분을 하면 그 결과로 자기 자신이 나온다.
4.3. Trigonometric Functions, Sine and Cosine(삼각함수)

- sin을 미분하면 cos이다.
- cos을 미분하면 -sin이다.
- -sin을 미분하면 -cos이다.
- -cos을 미분하면 다시 sin으로 돌아온다.
즉 네 번을 주기로 미분의 결과가 반복된다는 것을 알 수 있다.
5. Let's differentiate some functions
- 다항함수 미분(1문제)
- 분수함수 미분(1문제)
- 지수함수 + 삼각함수 미분(1문제)
- 정적분(1문제)
- 무리함수 미분(1문제)
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 1주차' 카테고리의 다른 글
| Time saving rules (2) | 2022.09.24 |
|---|---|
| Back to basics: functions (1) | 2022.09.23 |
