목차
1. Product rule
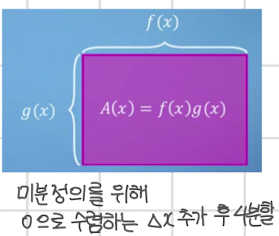

- A(x)를 원래의 보라색 사각형을 제외한 나머지 세 부분을 합친 것으로 정의한다.
- 델타 x가 0으로 수렴하면 흰색 사각형의 면적은 0이 되므로 사라진다.
- 남은 초록색과 노란색 사각형의 면적에 대한 식으로 정리하고 양 변을 델타 x로 나눈다.
이는 미분의 정의에 맞게끔 식을 조정하는 과정이다. - 마지막으로 식을 쪼갠 뒤 f(x)와 g(x)를 나누고 델타 x를 0으로 수렴하게 만들면 미분의 정의에 의해 마지막 식이 도출된다.
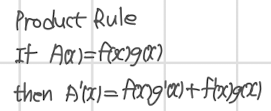
- 위 내용을 정리하면 Product Rule, 곱 규칙이 되고 식은 위와 같다.
곱의 미분 = 앞미분 + 뒷미분
2. Practicing the product rule
- product rule의 정의(2문제)
'세 개를 연속으로 곱하는 경우는 어떻게 되는가'
; 마찬가지로 하나씩 미분한 결과를 더 한 세 항의 합으로 표현된다. - 다항함수의 곱 미분(1문제)
- 다항함수, 삼각함수의 곱 미분(1문제)
- 자연지수함수, 유리함수의 곱 미분(1문제)
- 다항함수, 자연지수함수, 삼각함수의 곱 미분(1문제)
3. Chain rule
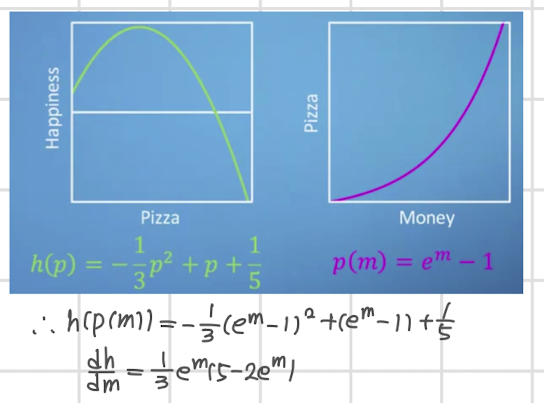
- 다항함수 h의 변수로 자연지수함수 p를 주게 되면 이것의 미분은 어떻게 되는지 확인해보고자 한다.
- 따라서 h의 변수 p 대신 p(m) 을 사용한 식이 전개 되어있다.
- 둘의 그래프를 각각 그리면 위와 같다.

- 여기서는 chain rule(연쇄법칙)을 증명하지는 않았다.
- 합성함수의 경우 변수를 바꾸어 표현하지 않더라도 각 함수를 미분한 결과를 곱해줌으로써 도함수를 구할 수 있다.
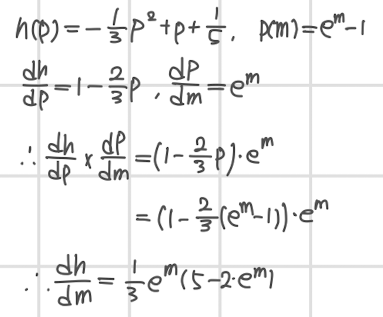
- h를 p에 대해 p를 m에 대해 각각 미분한다.
- 그 결과를 곱해준다.
- 우리가 구하고자 하는 것은 h를 m에 대해 미분한 것이므로, 남아있는 p를 m에 대한 식으로 치환하면 된다.
- 이를 통해 연쇄법칙을 확인할 수 있다.

- 연쇄법칙을 통해 구한 h(appiness)와 m(oney)의 관계를 그래프로 그린 것이 노란색이다.
4. Taming a beast

- 굉장히 복잡해보이는 위의 함수 f도 chain rule을 통해 간단히 정리할 수 있다.
- f를 두 함수 g,h로 나눈 뒤에 각각의 도함수를 구한다.
이 도함수를 합치는 것이 chain rule이다.
두 함수 g,h의 곱을 미분하는 것이기 때문이다. - g를 미분하는 경우 삼각함수의 미분과 다항함수의 미분이 섞여있다.
h를 미분하는 경우 자연지수함수와 다항함수의 미분이 섞여있다.
5. Practicing the chain rule
- 함성함수의 미분(1문제)
- 일반적인 함성함수의 미분을 연쇄법칙으로 풀이할 수 있다.
- 약간 어색하게 보이긴하지만 g(h) = g(h(x)) 로 풀이하면 이해된다.
- 자연지수함수의 미분(1문제)
- 밑은 자연상수, 지수는 다항식인 문제다. 따라서 연쇄법칙을 통해 풀이하도록 한다.
- 삼각함수의 미분(1문제)
- 삼각함수를 세제곱한 함수를 미분하는 문제
- tan(x)를 미분하는 문제
- 이 문제는 여러가지 풀이가 존재한다. 기본적으로 tan = sin / cos 임을 이용한다.
- 1) 연쇄법칙: sin과 cos의 역수를 각각 함수 f, g로 두고 연쇄법칙을 적용하여 f', g'을 구한다. 이후 곱의 미분법을 적용한다.
- 2) 몫의 미분법: 분자의 sin과 분모의 cos을 각각 함수 f, g로 두고 f / g 꼴의 몫의 미분법을 적용한다.
이때 결과물은 (f'g - fg') / g^2 이 된다. - 3) 곱의 미분법: sin과 cos의 역수를 각각 함수 f, g로 두고 곱의 미분법을 적용한다.(틀린 풀이)
이 풀이에서 주의할 점은 1/cos 을 미분한 것은 1/x 를 미분하는 것과 다른 결과로 나타난다는 것이다.
변수가 아닌 함수가 분모로 들어간 경우는 몫의 미분법을 적용해야 한다.
마찬가지로 분모가 cos이고 분자가 sin이므로 f / g 꼴의 몫의 미분법을 적용해야 한다.
요약하면 곱의 미분법을 적용하는 것 자체가 몫의 미분법을 쓰겠다는 뜻이다.
- 삼중첩 미분: 자연상수의 지수함수, 이때 지수는 삼각함수이고 삼각함수의 변수는 다항식
- 연쇄법칙을 적용하여 풀이하면 된다.
이때 우리가 구하고 싶은 것은 df / dx , f를 x에 대해 미분한 것이므로 변수 g, h가 남아있다면 전부 x로 표현될 수 있도록 해야 한다.
- 연쇄법칙을 적용하여 풀이하면 된다.
6. Unleahshing the toolbox
- Sum Rule 적용하기(1문제)
- 세 개의 항을 합친 함수를 미분한 결과를 구한다.
이때는 각각을 미분한 결과를 합치면 된다. - Power Rule도 활용된다.
- 세 개의 항을 합친 함수를 미분한 결과를 구한다.
- Product Rule(1문제)
- 어떤 함수가 여러 함수의 곱으로 표현된 경우, 각 함수를 하나씩 미분한 결과들을 더하면 된다.
- Chain Rule(3문제)
- 단순 연쇄법칙 하나만 적용해서 풀 수 있는 문제 한 개와 곱의 미분까지 적용해야 풀 수 있는 문제 두 개가 있다.
- 이 중 하나는 삼각함수로 구성되어 변수에 파이(180도)를 집어 넣어 식을 간단하게 만드는 것이 목표이다.
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 1주차' 카테고리의 다른 글
| Gradients and derivatives (2) | 2022.09.23 |
|---|---|
| Back to basics: functions (1) | 2022.09.23 |
1. Product rule


- A(x)를 원래의 보라색 사각형을 제외한 나머지 세 부분을 합친 것으로 정의한다.
- 델타 x가 0으로 수렴하면 흰색 사각형의 면적은 0이 되므로 사라진다.
- 남은 초록색과 노란색 사각형의 면적에 대한 식으로 정리하고 양 변을 델타 x로 나눈다.
이는 미분의 정의에 맞게끔 식을 조정하는 과정이다. - 마지막으로 식을 쪼갠 뒤 f(x)와 g(x)를 나누고 델타 x를 0으로 수렴하게 만들면 미분의 정의에 의해 마지막 식이 도출된다.
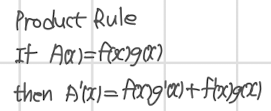
- 위 내용을 정리하면 Product Rule, 곱 규칙이 되고 식은 위와 같다.
곱의 미분 = 앞미분 + 뒷미분
2. Practicing the product rule
- product rule의 정의(2문제)
'세 개를 연속으로 곱하는 경우는 어떻게 되는가'
; 마찬가지로 하나씩 미분한 결과를 더 한 세 항의 합으로 표현된다. - 다항함수의 곱 미분(1문제)
- 다항함수, 삼각함수의 곱 미분(1문제)
- 자연지수함수, 유리함수의 곱 미분(1문제)
- 다항함수, 자연지수함수, 삼각함수의 곱 미분(1문제)
3. Chain rule

- 다항함수 h의 변수로 자연지수함수 p를 주게 되면 이것의 미분은 어떻게 되는지 확인해보고자 한다.
- 따라서 h의 변수 p 대신 p(m) 을 사용한 식이 전개 되어있다.
- 둘의 그래프를 각각 그리면 위와 같다.

- 여기서는 chain rule(연쇄법칙)을 증명하지는 않았다.
- 합성함수의 경우 변수를 바꾸어 표현하지 않더라도 각 함수를 미분한 결과를 곱해줌으로써 도함수를 구할 수 있다.
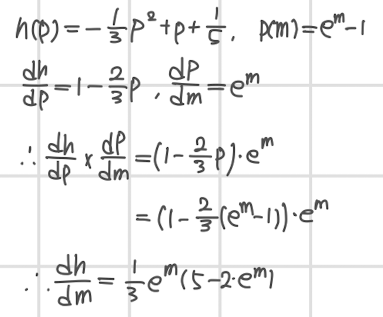
- h를 p에 대해 p를 m에 대해 각각 미분한다.
- 그 결과를 곱해준다.
- 우리가 구하고자 하는 것은 h를 m에 대해 미분한 것이므로, 남아있는 p를 m에 대한 식으로 치환하면 된다.
- 이를 통해 연쇄법칙을 확인할 수 있다.

- 연쇄법칙을 통해 구한 h(appiness)와 m(oney)의 관계를 그래프로 그린 것이 노란색이다.
4. Taming a beast

- 굉장히 복잡해보이는 위의 함수 f도 chain rule을 통해 간단히 정리할 수 있다.
- f를 두 함수 g,h로 나눈 뒤에 각각의 도함수를 구한다.
이 도함수를 합치는 것이 chain rule이다.
두 함수 g,h의 곱을 미분하는 것이기 때문이다. - g를 미분하는 경우 삼각함수의 미분과 다항함수의 미분이 섞여있다.
h를 미분하는 경우 자연지수함수와 다항함수의 미분이 섞여있다.
5. Practicing the chain rule
- 함성함수의 미분(1문제)
- 일반적인 함성함수의 미분을 연쇄법칙으로 풀이할 수 있다.
- 약간 어색하게 보이긴하지만 g(h) = g(h(x)) 로 풀이하면 이해된다.
- 자연지수함수의 미분(1문제)
- 밑은 자연상수, 지수는 다항식인 문제다. 따라서 연쇄법칙을 통해 풀이하도록 한다.
- 삼각함수의 미분(1문제)
- 삼각함수를 세제곱한 함수를 미분하는 문제
- tan(x)를 미분하는 문제
- 이 문제는 여러가지 풀이가 존재한다. 기본적으로 tan = sin / cos 임을 이용한다.
- 1) 연쇄법칙: sin과 cos의 역수를 각각 함수 f, g로 두고 연쇄법칙을 적용하여 f', g'을 구한다. 이후 곱의 미분법을 적용한다.
- 2) 몫의 미분법: 분자의 sin과 분모의 cos을 각각 함수 f, g로 두고 f / g 꼴의 몫의 미분법을 적용한다.
이때 결과물은 (f'g - fg') / g^2 이 된다. - 3) 곱의 미분법: sin과 cos의 역수를 각각 함수 f, g로 두고 곱의 미분법을 적용한다.(틀린 풀이)
이 풀이에서 주의할 점은 1/cos 을 미분한 것은 1/x 를 미분하는 것과 다른 결과로 나타난다는 것이다.
변수가 아닌 함수가 분모로 들어간 경우는 몫의 미분법을 적용해야 한다.
마찬가지로 분모가 cos이고 분자가 sin이므로 f / g 꼴의 몫의 미분법을 적용해야 한다.
요약하면 곱의 미분법을 적용하는 것 자체가 몫의 미분법을 쓰겠다는 뜻이다.
- 삼중첩 미분: 자연상수의 지수함수, 이때 지수는 삼각함수이고 삼각함수의 변수는 다항식
- 연쇄법칙을 적용하여 풀이하면 된다.
이때 우리가 구하고 싶은 것은 df / dx , f를 x에 대해 미분한 것이므로 변수 g, h가 남아있다면 전부 x로 표현될 수 있도록 해야 한다.
- 연쇄법칙을 적용하여 풀이하면 된다.
6. Unleahshing the toolbox
- Sum Rule 적용하기(1문제)
- 세 개의 항을 합친 함수를 미분한 결과를 구한다.
이때는 각각을 미분한 결과를 합치면 된다. - Power Rule도 활용된다.
- 세 개의 항을 합친 함수를 미분한 결과를 구한다.
- Product Rule(1문제)
- 어떤 함수가 여러 함수의 곱으로 표현된 경우, 각 함수를 하나씩 미분한 결과들을 더하면 된다.
- Chain Rule(3문제)
- 단순 연쇄법칙 하나만 적용해서 풀 수 있는 문제 한 개와 곱의 미분까지 적용해야 풀 수 있는 문제 두 개가 있다.
- 이 중 하나는 삼각함수로 구성되어 변수에 파이(180도)를 집어 넣어 식을 간단하게 만드는 것이 목표이다.
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 1주차' 카테고리의 다른 글
| Gradients and derivatives (2) | 2022.09.23 |
|---|---|
| Back to basics: functions (1) | 2022.09.23 |
