목차
1. The Sandpit

- 간단한 함수에 대해서는 값이 최대가 되는 좌표가 어디인지 파악하기가 쉽다.
위 그래프는 Jacobian vector를 통해 표현한 것이다.
그러나 대부분은 이렇게 간단하지는 않다.
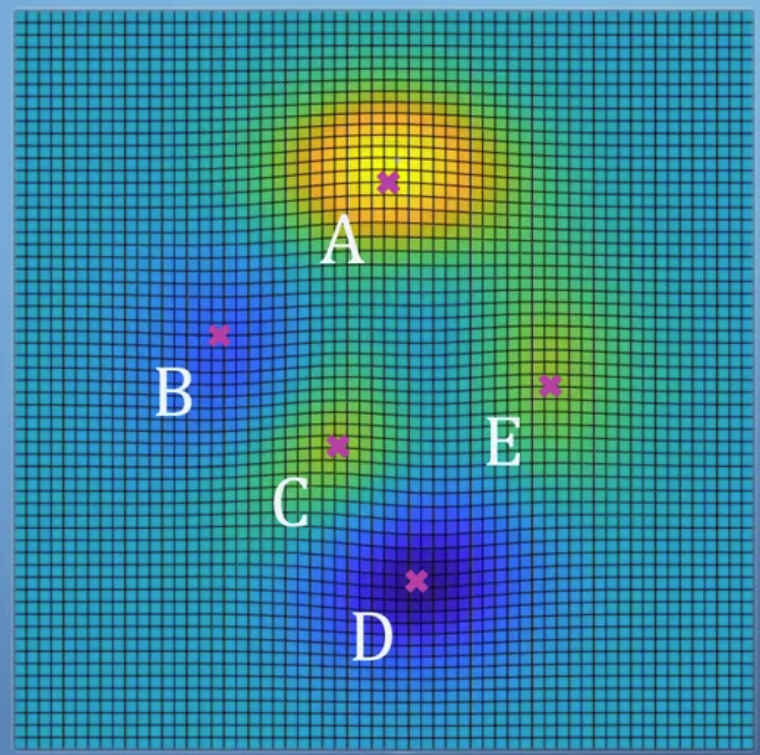
- 앞서 다루었던 복잡한 식을 표현하면 위와 같다.
여기서는 global maximum A와 local maximum C,E가 존재한다.
반대로 global minimum D와 local minimum B가 존재한다.
얼마나 가파른지에 대한(gradient) 정보를 각 좌표를 기준으로 표시하면 아래 그래프와 같다.
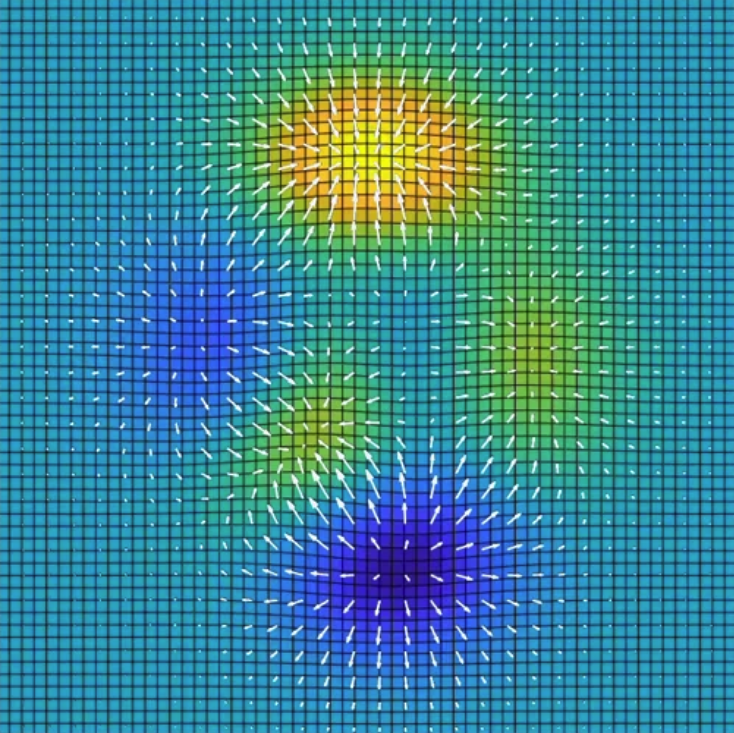
- 우리는 모든 것을 관망하는 입장에서 어디로 가야 가장 높은지 혹은 가장 낮은지를 알 수 있다.
하지만 실제로는 모든 데이터에 대한 정보를 파악하고 미리 알 수는 없으므로 마치 밤길을 거니는 것과 동일하다.
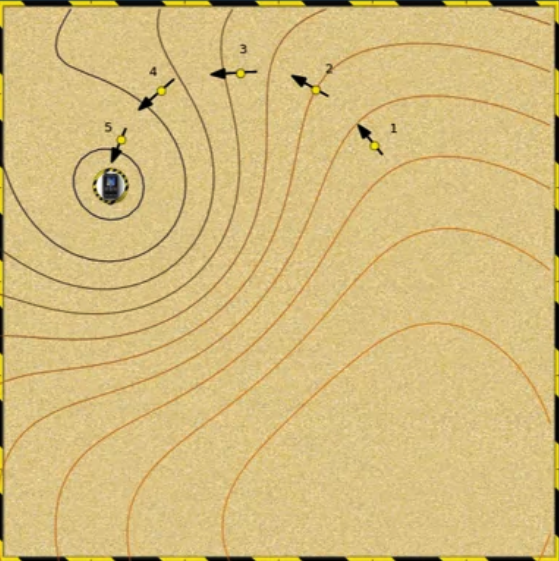
- 이를 모래구덩이 게임에 비유할 수 있다.
- 이렇게 특정 포인트에 잘못 빠질 수 있다는 점이 우리가 앞으로 만날 optimization(최적화)에서의 문제점이다.
2. The Sandpit - Part 1,2
- 주피터 노트북을 통해 실제 Sandpit game을 통해 gradient descent에 대한 intuition을 높이도록 했다.
- Jacovian vector 없이 정확한 global minimum을 찾는 것이란 사실상 불가능에 가깝다(사방팔방 다 찍어야 된다.)
- Contour(등고선)가 꼬여있는 경우 벡터가 서로 반대 방향으로 어지럽게 얽힌다.
- 지나치게 깊은 local minimum이 있는 경우 찾기가 더욱 어렵다.
3. The Hessian

- 벡터로 표현되는 Jacobian에서 편미분을 한 번 더 수행하여 matrix로 표현한 것이 Hessian이다.

- Hessian은 symmetrical(대칭적)하며 행렬식을 통해 공간의 모양새를 파악할 수 있게 도와준다.
- 공간의 모양새라는 것은 공간의 높고 낮음을 의미한다.

- Jacobian만 가지고는 어느 지점이 최대 혹은 최소인지 파악하기 어렵다.
- 물론 다른 모든 포인트에 대해서 값을 대입해보면 알 수 있지만 굉장히 불편한 과정이다.
- Hessian의 determinant(행렬식)이 4이고 이것이 곧 minimum이 된다.
- 만약 Hessian의 (0,0)의 값이 음수라면 이 행렬의 행렬식은 maximum이 된다
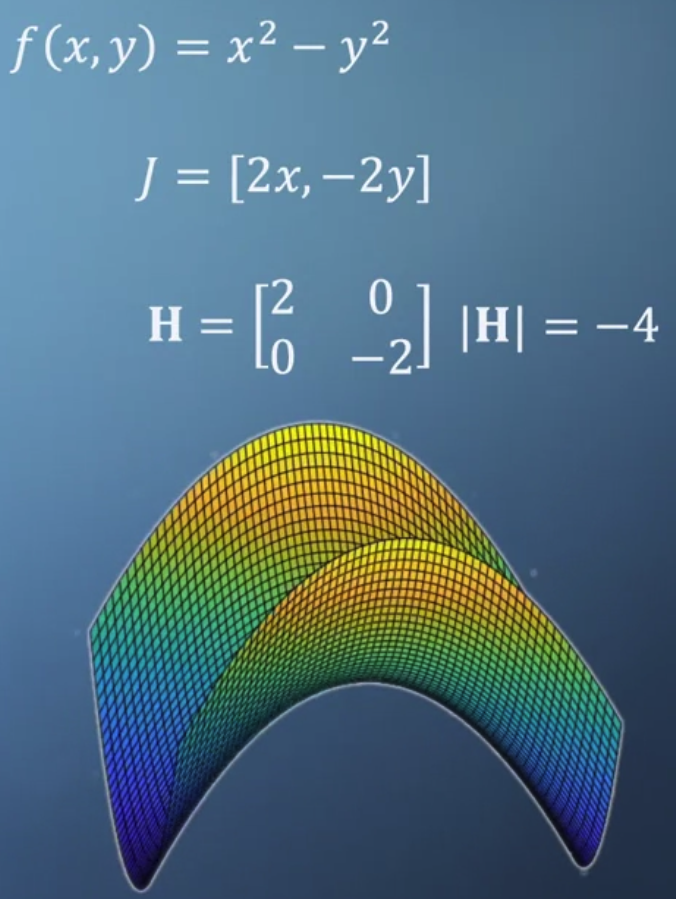
- 이 함수에 대한 Hessian을 구하고 이것의 행렬식을 구하면 음수가 나온다.
이 경우는 saddle(말의 안장)이라고 하며 peak를 찾기 굉장히 어려운 형태 중 하나다.
4. Calculating Hessians
- 2,3차원 Hessian matrix 구하기(5문제)
5. Reality is hard
1) 실제 matrix를 다룰 때는 2,3차원이 아닌 수백, 수천 차원에 대해 다루기 때문에 수학적으로밖에 접근할 수 없다.
2) 2차원에 대한 문제를 다룰지라도 모든 포인트에 대해 값을 계산하는 것은 굉장히 많은 비용을 요구한다.
3) 실제로는 결과에 noise가 생기도록 하는 많은 요인들이 존재한다. 예를 들면 함수의 불연속성이 그렇다.
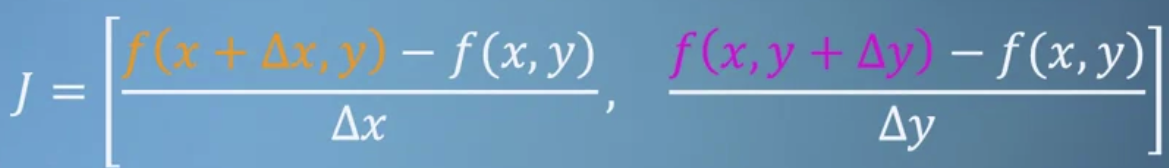
- 따라서 미분의 개념을 Jacobian에도 적용한다.
모든 포인트에 대해 계산하지 않고 일부만 가지고 계산을 수행하는 것이다.
이때 주의할 점이 있다.- 1) x 또는 y의 변화량이 너무 작으면 컴퓨터에서 계산이 불가능하다.
어떤 변화도 생기지 않는 것이다. - 2) data에 noise가 존재하는 경우 계산이 어려워진다.
이때는 여러 step에 대해 gradient를 계산하고 이것들의 평균을 구하는 방식을 취한다(가장 기본적인 방법).
- 1) x 또는 y의 변화량이 너무 작으면 컴퓨터에서 계산이 불가능하다.
6. Assessment: Jacobians and Hessians
- Jacobian 또는 Hessian을 구하고 특정 포인트 대입하기(5문제)
- 편미분(다른 변수를 상수 취급)에만 유의하여 식을 전개하면 어려운 것은 아니다.
- 삼각함수 미분이 반복된다는 것을 꼭 기억해두자. sin → cos → -sin → -cos (cos을 미분하면 음수가 된다)
- Jacobian은 vector고 Hessian은 matrix라서 값이라는 표현이 정확하지는 않은데 뭐라고 해야할지 모르겠다 😅
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 2주차' 카테고리의 다른 글
| Jacobians - vectors of derivatives (0) | 2022.09.29 |
|---|---|
| Moving to multivariate (2) | 2022.09.29 |
1. The Sandpit

- 간단한 함수에 대해서는 값이 최대가 되는 좌표가 어디인지 파악하기가 쉽다.
위 그래프는 Jacobian vector를 통해 표현한 것이다.
그러나 대부분은 이렇게 간단하지는 않다.

- 앞서 다루었던 복잡한 식을 표현하면 위와 같다.
여기서는 global maximum A와 local maximum C,E가 존재한다.
반대로 global minimum D와 local minimum B가 존재한다.
얼마나 가파른지에 대한(gradient) 정보를 각 좌표를 기준으로 표시하면 아래 그래프와 같다.

- 우리는 모든 것을 관망하는 입장에서 어디로 가야 가장 높은지 혹은 가장 낮은지를 알 수 있다.
하지만 실제로는 모든 데이터에 대한 정보를 파악하고 미리 알 수는 없으므로 마치 밤길을 거니는 것과 동일하다.

- 이를 모래구덩이 게임에 비유할 수 있다.
- 이렇게 특정 포인트에 잘못 빠질 수 있다는 점이 우리가 앞으로 만날 optimization(최적화)에서의 문제점이다.
2. The Sandpit - Part 1,2
- 주피터 노트북을 통해 실제 Sandpit game을 통해 gradient descent에 대한 intuition을 높이도록 했다.
- Jacovian vector 없이 정확한 global minimum을 찾는 것이란 사실상 불가능에 가깝다(사방팔방 다 찍어야 된다.)
- Contour(등고선)가 꼬여있는 경우 벡터가 서로 반대 방향으로 어지럽게 얽힌다.
- 지나치게 깊은 local minimum이 있는 경우 찾기가 더욱 어렵다.
3. The Hessian

- 벡터로 표현되는 Jacobian에서 편미분을 한 번 더 수행하여 matrix로 표현한 것이 Hessian이다.

- Hessian은 symmetrical(대칭적)하며 행렬식을 통해 공간의 모양새를 파악할 수 있게 도와준다.
- 공간의 모양새라는 것은 공간의 높고 낮음을 의미한다.

- Jacobian만 가지고는 어느 지점이 최대 혹은 최소인지 파악하기 어렵다.
- 물론 다른 모든 포인트에 대해서 값을 대입해보면 알 수 있지만 굉장히 불편한 과정이다.
- Hessian의 determinant(행렬식)이 4이고 이것이 곧 minimum이 된다.
- 만약 Hessian의 (0,0)의 값이 음수라면 이 행렬의 행렬식은 maximum이 된다
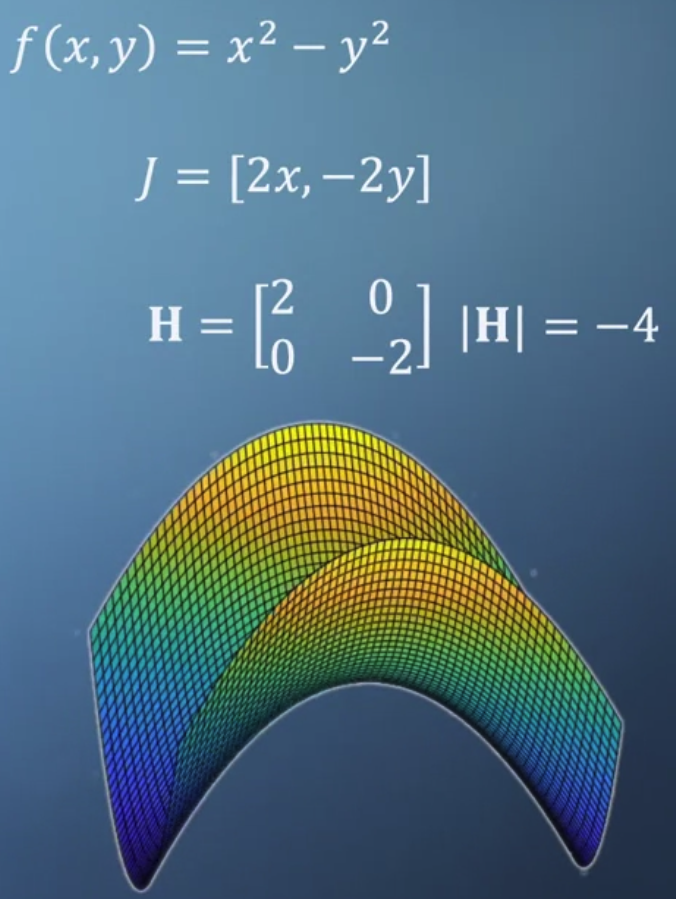
- 이 함수에 대한 Hessian을 구하고 이것의 행렬식을 구하면 음수가 나온다.
이 경우는 saddle(말의 안장)이라고 하며 peak를 찾기 굉장히 어려운 형태 중 하나다.
4. Calculating Hessians
- 2,3차원 Hessian matrix 구하기(5문제)
5. Reality is hard
1) 실제 matrix를 다룰 때는 2,3차원이 아닌 수백, 수천 차원에 대해 다루기 때문에 수학적으로밖에 접근할 수 없다.
2) 2차원에 대한 문제를 다룰지라도 모든 포인트에 대해 값을 계산하는 것은 굉장히 많은 비용을 요구한다.
3) 실제로는 결과에 noise가 생기도록 하는 많은 요인들이 존재한다. 예를 들면 함수의 불연속성이 그렇다.
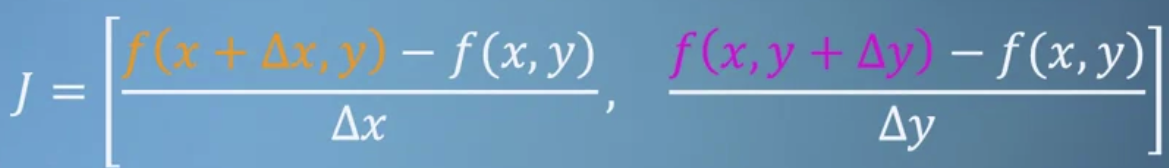
- 따라서 미분의 개념을 Jacobian에도 적용한다.
모든 포인트에 대해 계산하지 않고 일부만 가지고 계산을 수행하는 것이다.
이때 주의할 점이 있다.- 1) x 또는 y의 변화량이 너무 작으면 컴퓨터에서 계산이 불가능하다.
어떤 변화도 생기지 않는 것이다. - 2) data에 noise가 존재하는 경우 계산이 어려워진다.
이때는 여러 step에 대해 gradient를 계산하고 이것들의 평균을 구하는 방식을 취한다(가장 기본적인 방법).
- 1) x 또는 y의 변화량이 너무 작으면 컴퓨터에서 계산이 불가능하다.
6. Assessment: Jacobians and Hessians
- Jacobian 또는 Hessian을 구하고 특정 포인트 대입하기(5문제)
- 편미분(다른 변수를 상수 취급)에만 유의하여 식을 전개하면 어려운 것은 아니다.
- 삼각함수 미분이 반복된다는 것을 꼭 기억해두자. sin → cos → -sin → -cos (cos을 미분하면 음수가 된다)
- Jacobian은 vector고 Hessian은 matrix라서 값이라는 표현이 정확하지는 않은데 뭐라고 해야할지 모르겠다 😅
출처: Coursera, Mathematics for Machine Learning: Multivariate Calculus, Imperial College London.
'Multivariate Calculus > 2주차' 카테고리의 다른 글
| Jacobians - vectors of derivatives (0) | 2022.09.29 |
|---|---|
| Moving to multivariate (2) | 2022.09.29 |
