목차
1. Binary Classification
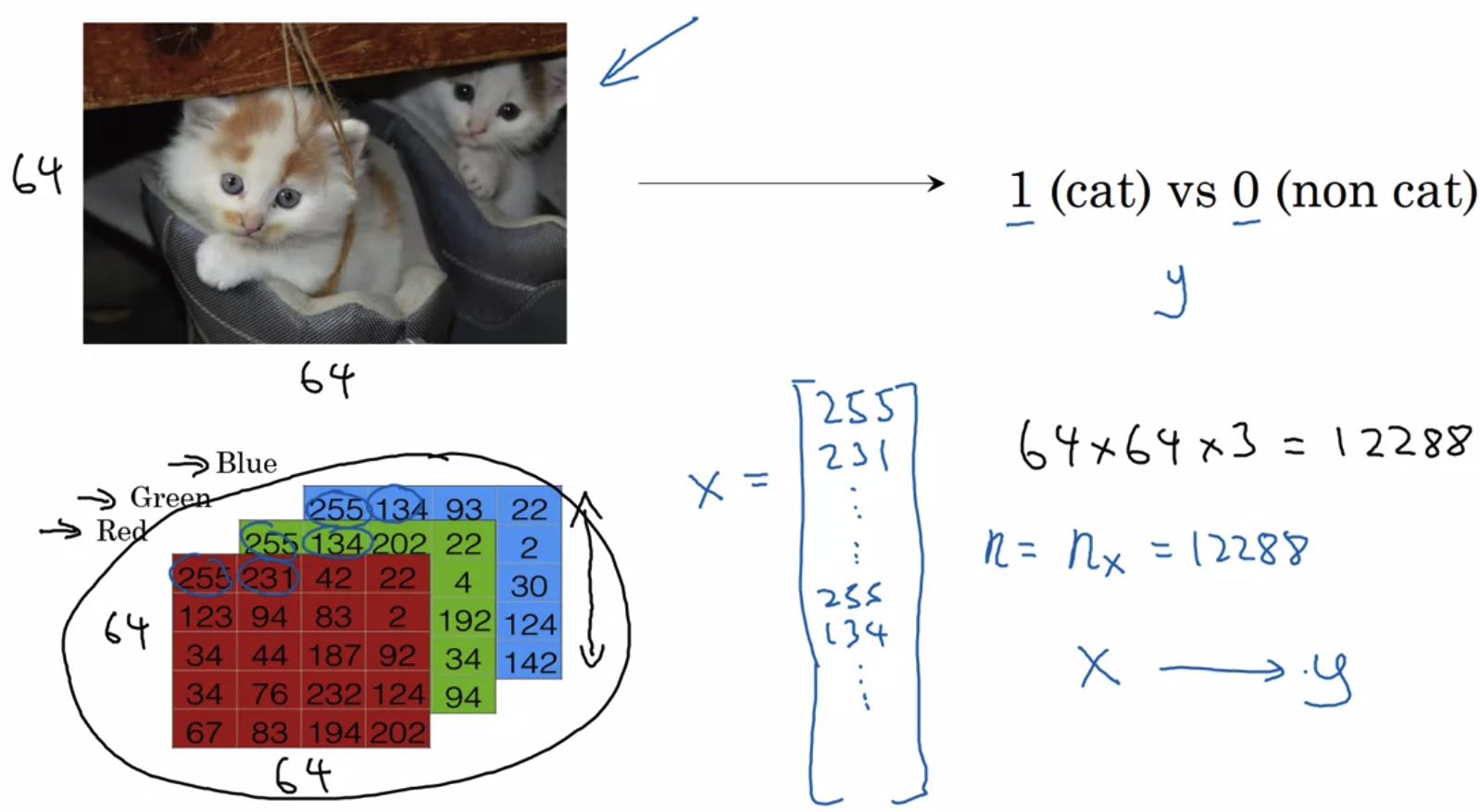
- binary classification(이진 분류)는 위와 같이 '~이다, ~가 아니다'로 구분하는 것이 예가 될 수 있다.
- 이미지는 Red, Green, Blue 세 가지의 정보를 담고 있는 세 개의 채널로 구성된다.
그 크기를 표현하면 3 x 64 x 64가 된다.(예시) - 이를 input X로 표현하면 12288(곱셈 결과)가 된다. 이것이 곧 차원이 된다.
Notation
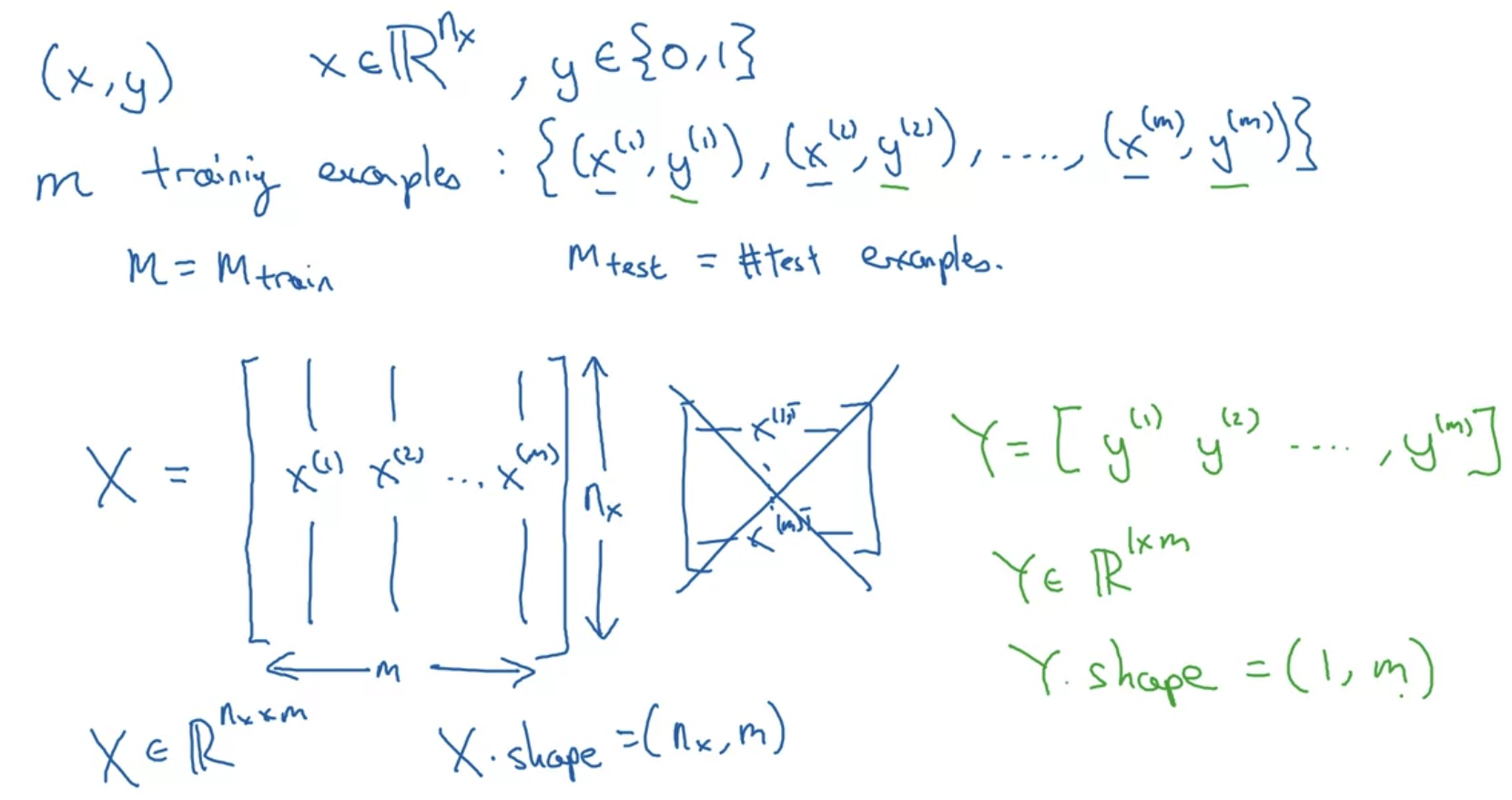
- input X는 nx차원에 속하고 정답 레이블(label)인 y는 0 또는 1로 이진 분류된다.
- training example m을 input과 label의 조합으로 생각하면
X를 m개의 열벡터 x로 구성된 행렬로, Y를 m개의 열벡터 y로 구성된 행렬로 생각할 수 있다. - 이에 따라서 행렬 X는 (nx x m) 의 size를 갖고, 행렬 Y는 (1, m) 사이즈를 갖는다.
2. Logistic Regression
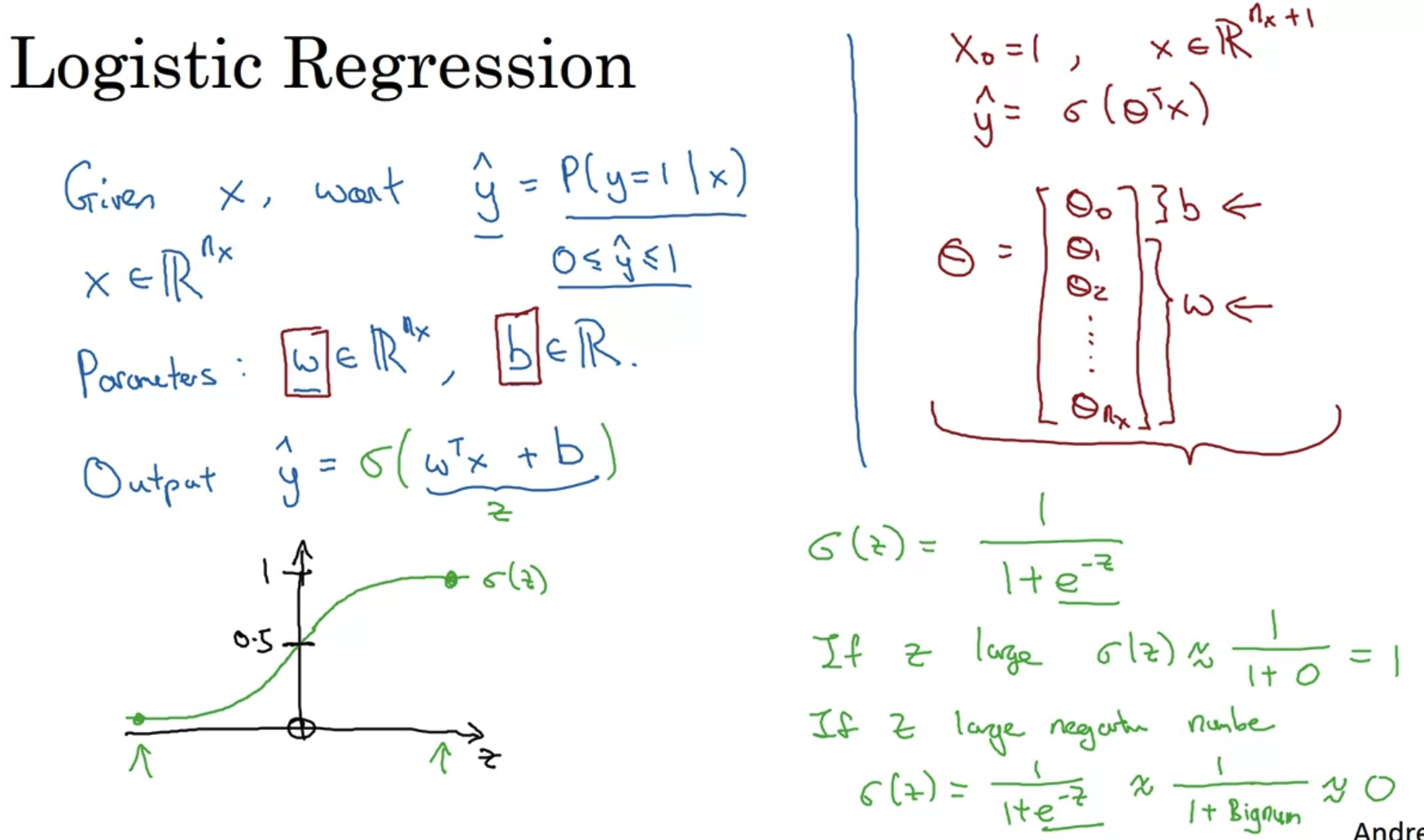
- Logistic Regression은 Linear Regression에서와 y hat의 의미가 다르다.
여기서는 input으로 X가 주어졌을 때 레이블이 1이 될 확률을 뜻하게 된다. - 하지만 Linear Regression에서 y hat을 Wx + b로 구했기 때문에 확률인 0에서 1범위를 벗어나는 값이 나올 수 있다.
따라서 이를 해결하기 위해 Wx + b에 sigmoid 함수를 적용하여 그 결과값이 0과 1 사이가 될 수 있도록 한다.
여기서 W는 nx 차원 벡터, b는 real number이다. - Sigmoid 함수의 특성상, input이 커지면 그 함수값은 1에 까가워지고, input이 작아지면 그 함수값은 0에 가까워진다.
- 가중치 W와 편향 b를 한꺼번에 묶어 표기하는 notation도 있지만 이 강의에서는 이처럼 표현하지 않음을 언급했다.
3. Logistic Regression Cost Function
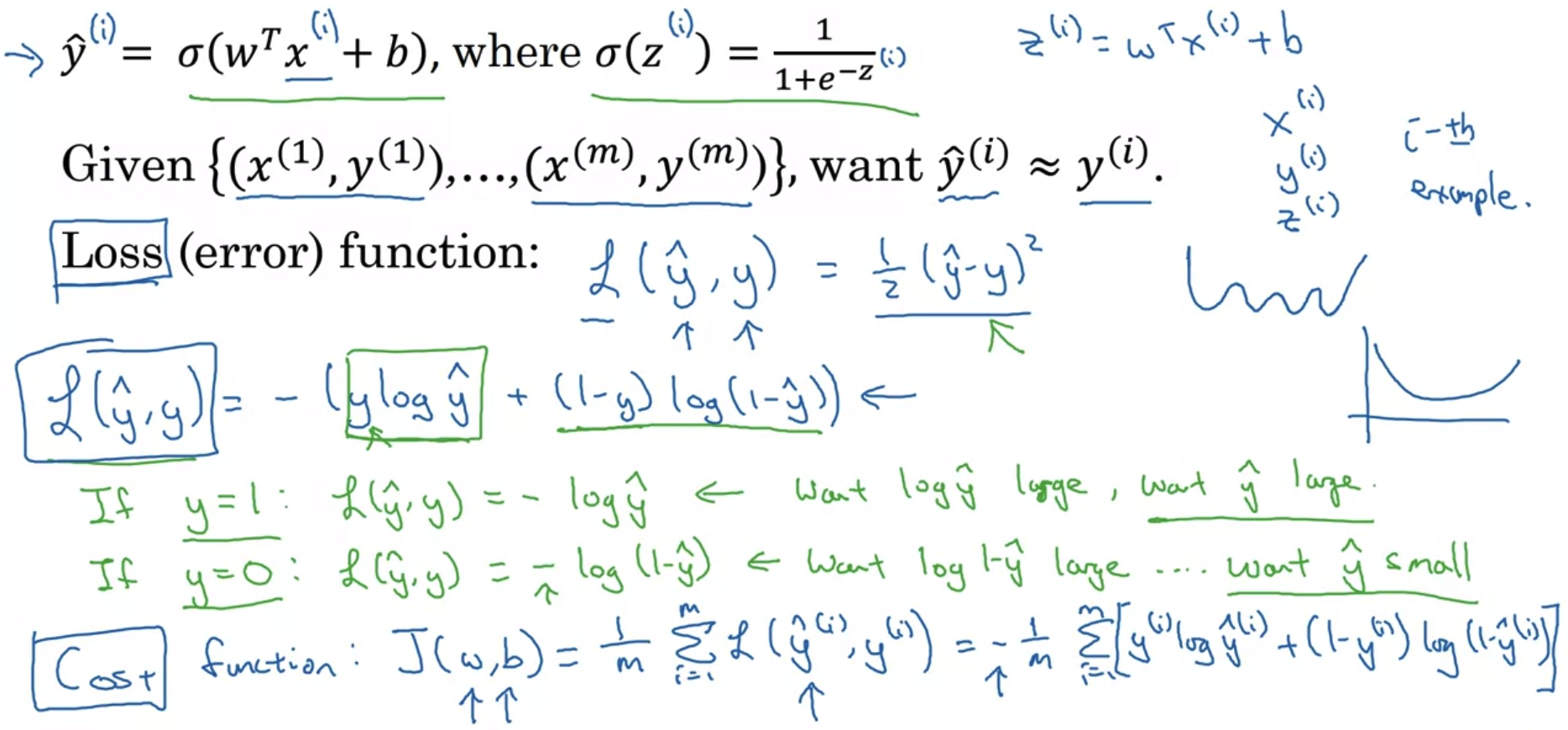
- Logistic Regression은 일종의 작은 Neural Network이다.
- Loss function은 training set 중 한 개의 example에 대한 식이고, Cost function은 모든 data set에 대한 식이다.
- 우리가 이 식을 통해 하고 싶은 것은 loss를 최소화하는 것이기 때문에 y의 값에 따라 최대화, 최소화 하고 싶은 값이 달라진다.
최종적으로 J(w,b)를 최소화하는 w,b를 찾아야 한다.
예를 들어 y = 1인 경우 - log (y hat)이 남게 되므로 y hat을 최대화해야 log (y hat)이 최대화되고 총 결과는 가장 작아지게 된다.
이때 y hat 은 sigmoid로 정의되므로 그 값의 범위는 0부터 1사이가 된다.
y = 1 이라면 우리가 만든 함수의 예측값인 y hat이 1이며 loss = 0이 되어야 한다는 의미가 된다.
하지만 이때 y hat = 0이 되면 loss는 무한대로 커져야 한다는 의미가 된다.
즉 실제 label과 예측값이 동일한 경우 loss = 0, 동일하지 않은 경우는 loss = ∞ 가 된다.
(y = 0 일 때는 정반대로 작동해야 된다.) - Cost function은 위에서 구한 Loss function의 정의에 따라 구한 모든 loss의 평균을 구하는 함수가 된다.
함수의 직관성을 위해 마이너스 부호는 식의 맨 앞으로 꺼내올 수 있다.
4. Gradient Descent
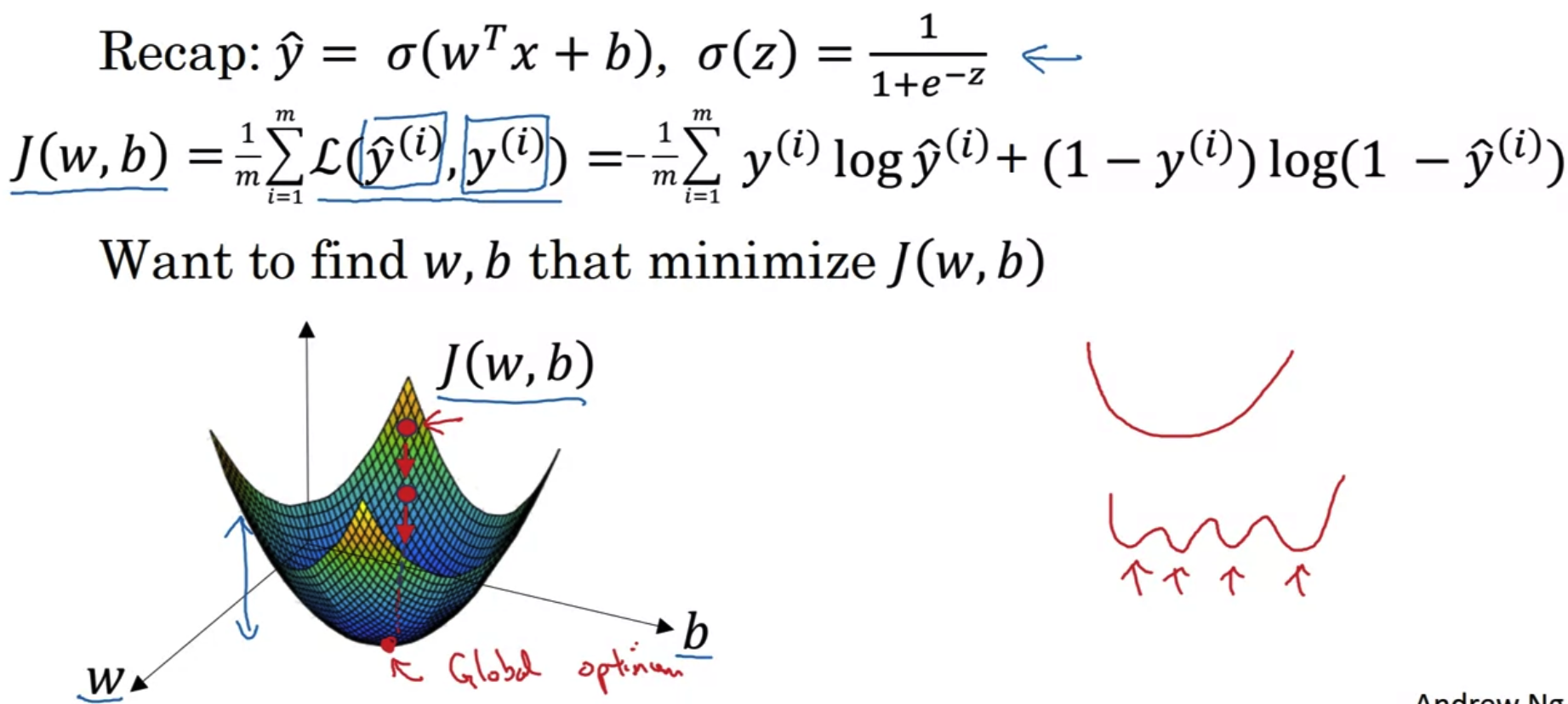
- 앞서 설명한 것처럼 Cost Function을 최소화하는 w,b를 찾는 것이 우리의 목표다.
따라서 w,b,J(w,b)를 각 축으로 삼아 3차원으로 표현한 것이 위의 그래프다.
(J(w,b)는 loss값이다) - Cost Function을 위와 같이 정의한 덕분에 위 그래프는 convex한 형태를 띠게 된다.
만약 convex하지 않고 여러 곳이 움푹 파여 있는 형태라면 local minimum에 갇힐 가능성이 있다.
하지만 convex한 형태의 그래프에서 값을 갱신하는 과정을 반복하면 어느 지점에서 initialize(초기화)하든지간에 반드시 global minimum(최저점)에 도달할 수 있다.
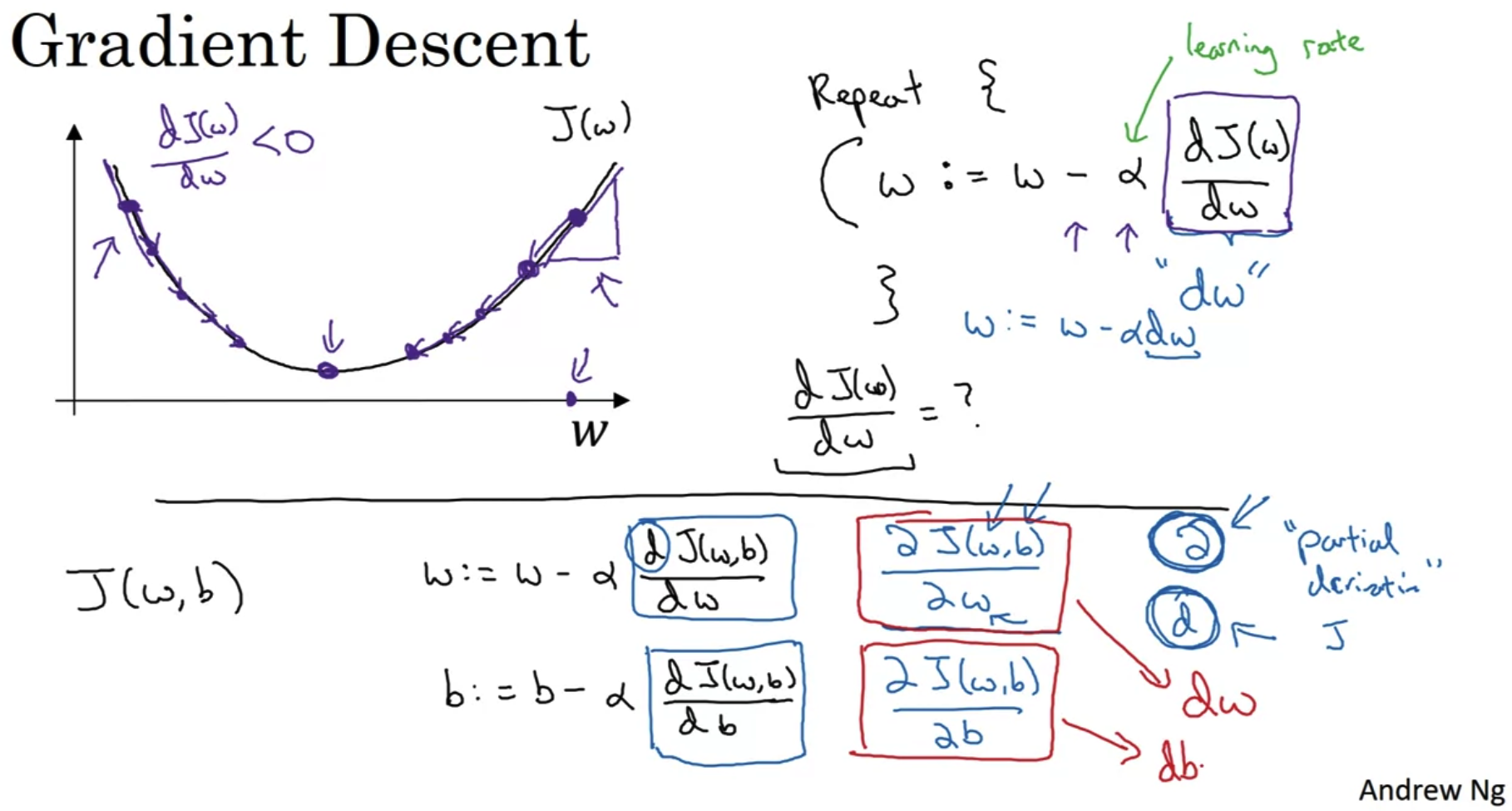
- 이해를 돕기 위해 편향 b를 제외한 변수인 가중치 w와 loss값 J(w)로 그래프를 그린 것은 위와 같다.
J(w)의 input이 w이므로, w의 값에 따라 J(w)의 값이 변하는 형태다. - α는 learning rate로 한 번에 업데이트하는 크기에 영향을 준다.
이후 강의에서 추가로 다룰 내용이다. - 우리가 원하는 것은 loss를 최소화하는 w의 값을 찾는 것이다.
이를 위해서 w를 계속해서 update 해줘야 하고, 이때 미분을 이용한다.
특정 w에 대해 미분 계수가(derivative) 양수인 경우, J(w) 값은 우리가 찾고자 하는 global minimum보다 큰 값이다.
따라서 w를 현재보다 작게 만들어야 우리의 목표점에 도달할 수 있다.
w의 값을 줄이는 과정을 반복하다보면 global minimum에 도착한다.
반대로 derivative가 음수인 경우, J(w)의 값은 우리가 찾고자 하는 global minimum보다 작은 값이다.
따라서 w를 현재보다 크게 만들어야 우리의 목표점에 도달할 수 있다.
이때 derivative는 음수이므로, 원래의 w에서 이 값을 빼야 w를 현재보다 크게 만들 수 있다.
마찬가지로 이 과정을 반복하면 global minimum 값을 갖는 w를 찾을 수 있게 된다. - 변수가 한 개인 어떤 함수에 대해 미분을 수행하는 기호는 dw로 나타낸다.
위 예시에서는 J(w) 함수에 대해 w를 기준으로 미분하겠다는 뜻이다.
만약 변수가 여러 개인(실제 loss는 w,b 두 개의 변수를 가진다) 함수에 대해 미분을 해야 하는 경우,
각 변수에 대해 미분을 수행해야 하고 이때 기호는 ∂를 사용한다.
∂J(w,b) / ∂w 는 J 함수를 w에 대해 미분한다는 뜻이다. 이를 b에 대해서도 수행하며 업데이트 해야 한다.
단, 이를 코드로 구현할 때는 변수가 한 개인 때와 마찬가지로 dw를 입력해야 한다.
5. Derivatives

- 직관적으로 미분은 함수에 대한 기울기를 나타낸다.
x축의 값에 해당하는 a를 아주 미세하게 늘린 것과 비교하여 기울기를 구할 수 있다.
예시로는 0.001 정도를 들었지만 사실은 이것보다 훨씬 작은 값을 이용하는 것으로 이해하면 된다. - 위 예시처럼 함수가 직선으로 표현되는 경우 어떤 input을 주더라도 거기에서의 기울기는 동일하다.
여기서는 기울기는 항상 3으로 a = 2이든 a = 5이든 동일한 derivative를 가지게 된다.
출처: Coursera, Neural Networks and Deep Learning, DeepLearning.AI
'Neural Networks and Deep Learning > 2주차' 카테고리의 다른 글
| Programming Assignments (2) | 2022.10.03 |
|---|---|
| Python and Vectorization(2) (0) | 2022.10.03 |
| Python and Vectorization(1) (0) | 2022.10.03 |
| Logistic Regression as a Neural Network(2) (1) | 2022.10.02 |
1. Binary Classification

- binary classification(이진 분류)는 위와 같이 '~이다, ~가 아니다'로 구분하는 것이 예가 될 수 있다.
- 이미지는 Red, Green, Blue 세 가지의 정보를 담고 있는 세 개의 채널로 구성된다.
그 크기를 표현하면 3 x 64 x 64가 된다.(예시) - 이를 input X로 표현하면 12288(곱셈 결과)가 된다. 이것이 곧 차원이 된다.
Notation

- input X는 nx차원에 속하고 정답 레이블(label)인 y는 0 또는 1로 이진 분류된다.
- training example m을 input과 label의 조합으로 생각하면
X를 m개의 열벡터 x로 구성된 행렬로, Y를 m개의 열벡터 y로 구성된 행렬로 생각할 수 있다. - 이에 따라서 행렬 X는 (nx x m) 의 size를 갖고, 행렬 Y는 (1, m) 사이즈를 갖는다.
2. Logistic Regression

- Logistic Regression은 Linear Regression에서와 y hat의 의미가 다르다.
여기서는 input으로 X가 주어졌을 때 레이블이 1이 될 확률을 뜻하게 된다. - 하지만 Linear Regression에서 y hat을 Wx + b로 구했기 때문에 확률인 0에서 1범위를 벗어나는 값이 나올 수 있다.
따라서 이를 해결하기 위해 Wx + b에 sigmoid 함수를 적용하여 그 결과값이 0과 1 사이가 될 수 있도록 한다.
여기서 W는 nx 차원 벡터, b는 real number이다. - Sigmoid 함수의 특성상, input이 커지면 그 함수값은 1에 까가워지고, input이 작아지면 그 함수값은 0에 가까워진다.
- 가중치 W와 편향 b를 한꺼번에 묶어 표기하는 notation도 있지만 이 강의에서는 이처럼 표현하지 않음을 언급했다.
3. Logistic Regression Cost Function
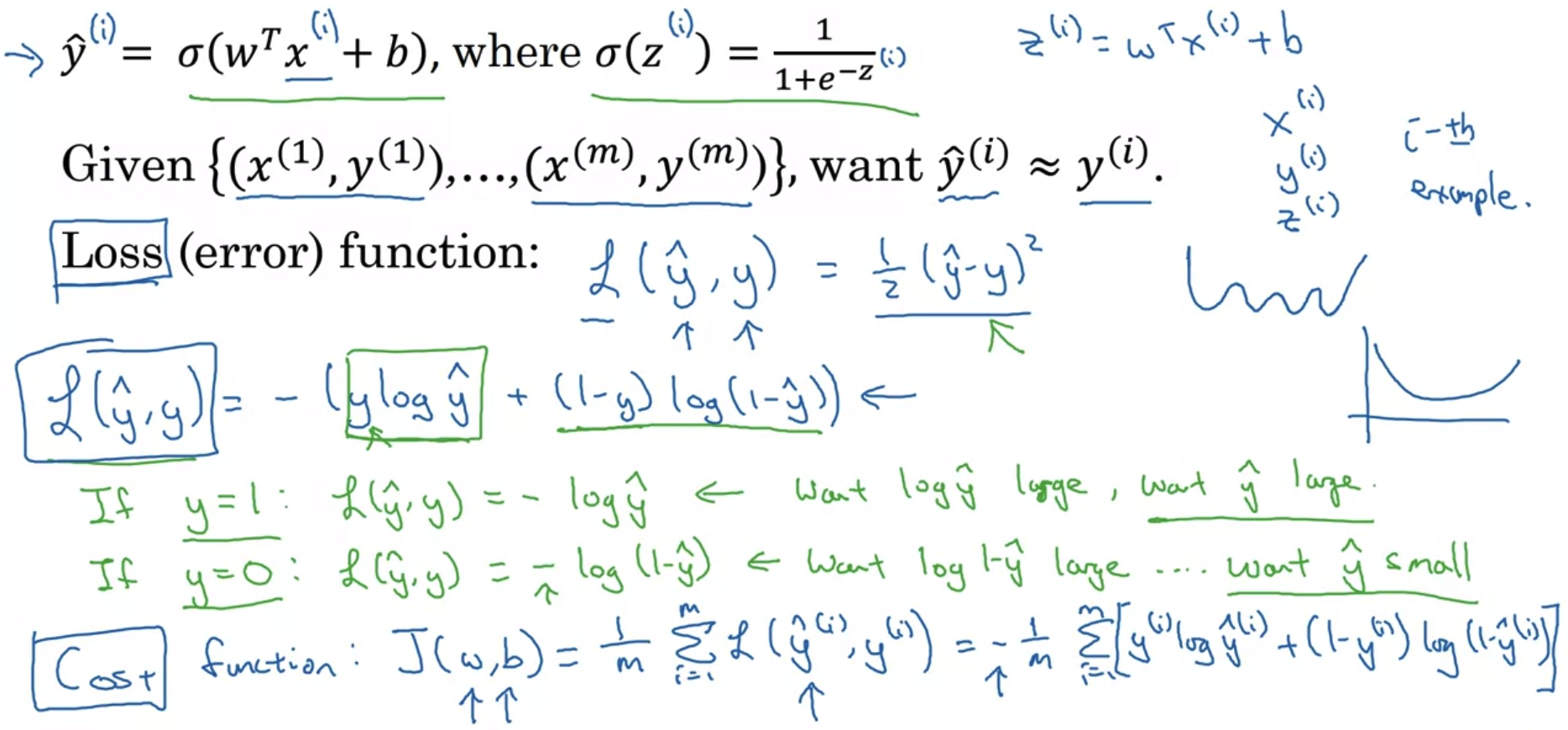
- Logistic Regression은 일종의 작은 Neural Network이다.
- Loss function은 training set 중 한 개의 example에 대한 식이고, Cost function은 모든 data set에 대한 식이다.
- 우리가 이 식을 통해 하고 싶은 것은 loss를 최소화하는 것이기 때문에 y의 값에 따라 최대화, 최소화 하고 싶은 값이 달라진다.
최종적으로 J(w,b)를 최소화하는 w,b를 찾아야 한다.
예를 들어 y = 1인 경우 - log (y hat)이 남게 되므로 y hat을 최대화해야 log (y hat)이 최대화되고 총 결과는 가장 작아지게 된다.
이때 y hat 은 sigmoid로 정의되므로 그 값의 범위는 0부터 1사이가 된다.
y = 1 이라면 우리가 만든 함수의 예측값인 y hat이 1이며 loss = 0이 되어야 한다는 의미가 된다.
하지만 이때 y hat = 0이 되면 loss는 무한대로 커져야 한다는 의미가 된다.
즉 실제 label과 예측값이 동일한 경우 loss = 0, 동일하지 않은 경우는 loss = ∞ 가 된다.
(y = 0 일 때는 정반대로 작동해야 된다.) - Cost function은 위에서 구한 Loss function의 정의에 따라 구한 모든 loss의 평균을 구하는 함수가 된다.
함수의 직관성을 위해 마이너스 부호는 식의 맨 앞으로 꺼내올 수 있다.
4. Gradient Descent

- 앞서 설명한 것처럼 Cost Function을 최소화하는 w,b를 찾는 것이 우리의 목표다.
따라서 w,b,J(w,b)를 각 축으로 삼아 3차원으로 표현한 것이 위의 그래프다.
(J(w,b)는 loss값이다) - Cost Function을 위와 같이 정의한 덕분에 위 그래프는 convex한 형태를 띠게 된다.
만약 convex하지 않고 여러 곳이 움푹 파여 있는 형태라면 local minimum에 갇힐 가능성이 있다.
하지만 convex한 형태의 그래프에서 값을 갱신하는 과정을 반복하면 어느 지점에서 initialize(초기화)하든지간에 반드시 global minimum(최저점)에 도달할 수 있다.

- 이해를 돕기 위해 편향 b를 제외한 변수인 가중치 w와 loss값 J(w)로 그래프를 그린 것은 위와 같다.
J(w)의 input이 w이므로, w의 값에 따라 J(w)의 값이 변하는 형태다. - α는 learning rate로 한 번에 업데이트하는 크기에 영향을 준다.
이후 강의에서 추가로 다룰 내용이다. - 우리가 원하는 것은 loss를 최소화하는 w의 값을 찾는 것이다.
이를 위해서 w를 계속해서 update 해줘야 하고, 이때 미분을 이용한다.
특정 w에 대해 미분 계수가(derivative) 양수인 경우, J(w) 값은 우리가 찾고자 하는 global minimum보다 큰 값이다.
따라서 w를 현재보다 작게 만들어야 우리의 목표점에 도달할 수 있다.
w의 값을 줄이는 과정을 반복하다보면 global minimum에 도착한다.
반대로 derivative가 음수인 경우, J(w)의 값은 우리가 찾고자 하는 global minimum보다 작은 값이다.
따라서 w를 현재보다 크게 만들어야 우리의 목표점에 도달할 수 있다.
이때 derivative는 음수이므로, 원래의 w에서 이 값을 빼야 w를 현재보다 크게 만들 수 있다.
마찬가지로 이 과정을 반복하면 global minimum 값을 갖는 w를 찾을 수 있게 된다. - 변수가 한 개인 어떤 함수에 대해 미분을 수행하는 기호는 dw로 나타낸다.
위 예시에서는 J(w) 함수에 대해 w를 기준으로 미분하겠다는 뜻이다.
만약 변수가 여러 개인(실제 loss는 w,b 두 개의 변수를 가진다) 함수에 대해 미분을 해야 하는 경우,
각 변수에 대해 미분을 수행해야 하고 이때 기호는 ∂를 사용한다.
∂J(w,b) / ∂w 는 J 함수를 w에 대해 미분한다는 뜻이다. 이를 b에 대해서도 수행하며 업데이트 해야 한다.
단, 이를 코드로 구현할 때는 변수가 한 개인 때와 마찬가지로 dw를 입력해야 한다.
5. Derivatives

- 직관적으로 미분은 함수에 대한 기울기를 나타낸다.
x축의 값에 해당하는 a를 아주 미세하게 늘린 것과 비교하여 기울기를 구할 수 있다.
예시로는 0.001 정도를 들었지만 사실은 이것보다 훨씬 작은 값을 이용하는 것으로 이해하면 된다. - 위 예시처럼 함수가 직선으로 표현되는 경우 어떤 input을 주더라도 거기에서의 기울기는 동일하다.
여기서는 기울기는 항상 3으로 a = 2이든 a = 5이든 동일한 derivative를 가지게 된다.
출처: Coursera, Neural Networks and Deep Learning, DeepLearning.AI
'Neural Networks and Deep Learning > 2주차' 카테고리의 다른 글
| Programming Assignments (2) | 2022.10.03 |
|---|---|
| Python and Vectorization(2) (0) | 2022.10.03 |
| Python and Vectorization(1) (0) | 2022.10.03 |
| Logistic Regression as a Neural Network(2) (1) | 2022.10.02 |
