1. More Derivative Examples

- 미분은 x축의 방향으로 아주 조금 움직였을 때 y축에서의 변화가 어떻게 될지 보여준다.
위 예시에서는 a의 값이 0.001(아주 작은 값)만큼 움직이면 f(a)는 얼만큼 움직이게 되는지 표현되어있다. - f(a)가 많이 움직일수록 그래프에서의 slope(경사)가 급한 것으로 이해할 수 있다.

- 위 예시들의 미분값을 보면 a에 따라서 그 미분값(slope)도 다르다는 것을 알 수 있다.
즉, 함수의 형태에 따라 미분값이 변화하는 정도나 패턴도 다르다는 것이다. - 어떤 식을 미분한 결과가 무엇인지 알지 모른다면 쉽게 검색하거나 교과서를 펼쳐보고 결과를 확인할 수 있다.
이전에 쌓아놓은 것이 없어 모른다면 검색해서 파악해두도록 하자.
2. Compuation Graph
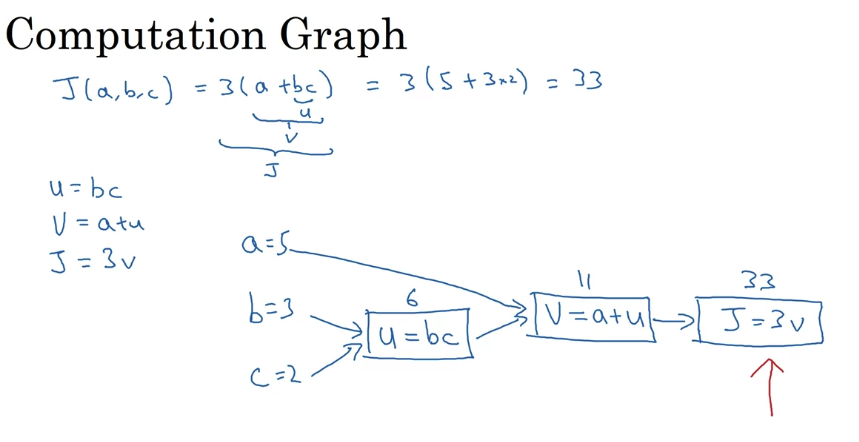
- left to right computation
- forward
- J라는 함수를 구성하는 변수들을 다른 변수로 치환하여 위처럼 시각화할 수 있다.
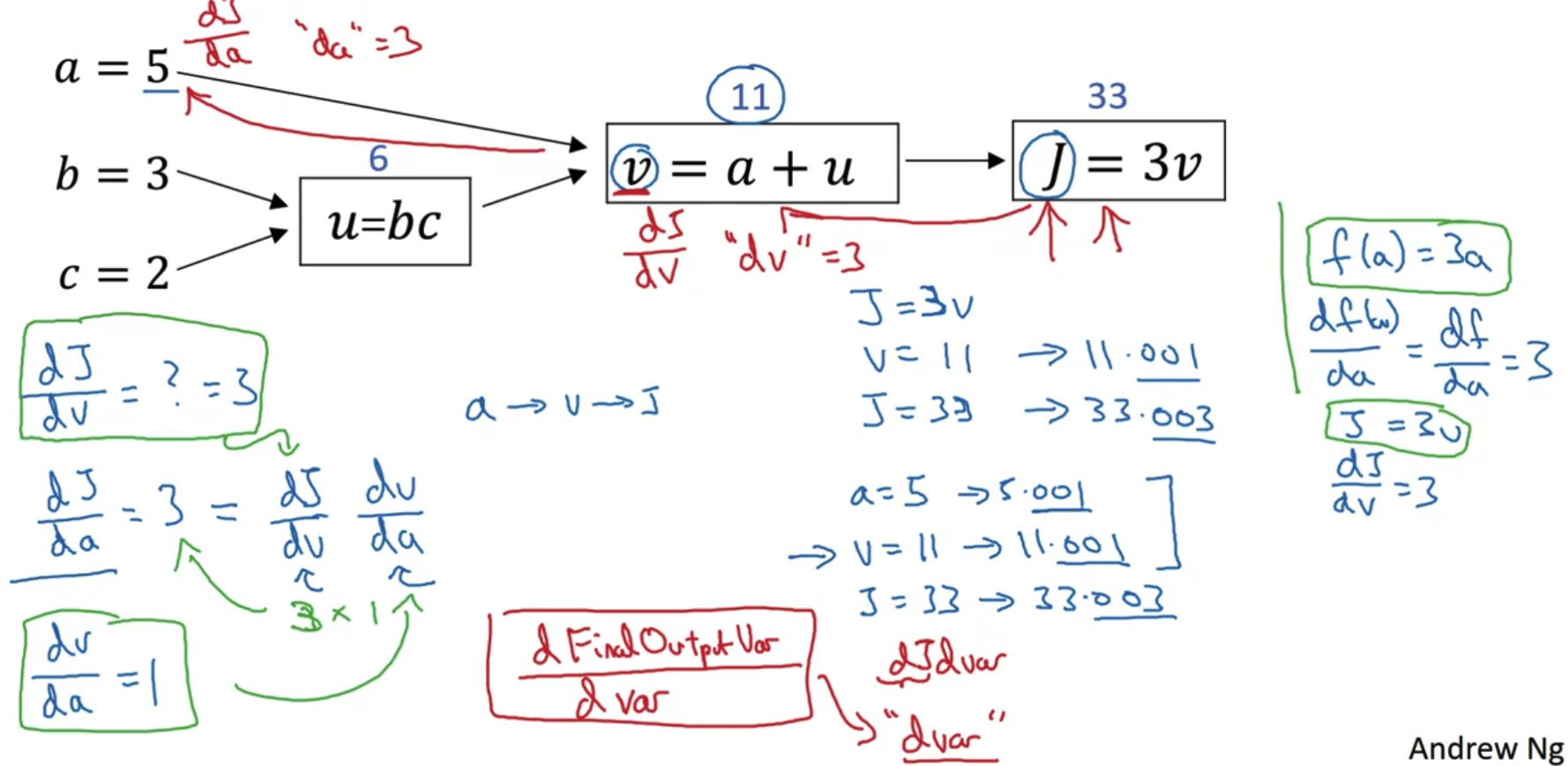
- a의 값을 바꾸면 v,J 가 영향을 받게 된다.
a의 값에 영향을 받는 정도를 우리가 위에서 계산한 기울기로 표현할 수 있다. - 반대로 생각해보면 결과물인 w 또는 J 를 보고 a의 영향을 얼마나 받았는지 확인하기 위해서는 이 기울기를 이용할 수 있다.
따라서 각 함수에 영향을 주는 변수를 거꾸로 하나씩 타고 내려가(편미분을 통해) 그 결과를 모두 곱하는 chain rule을 이용하여 back propagation을 수행한다. - 이런 내용을 코드로 구현할 때는 편미분을 할 때와 마찬가지로 dv 와 같은 방식으로 쓴다.
- 위 예시에서 FinalOutputVar은 J이고 Var는 a,v,u가 될 수 있다.
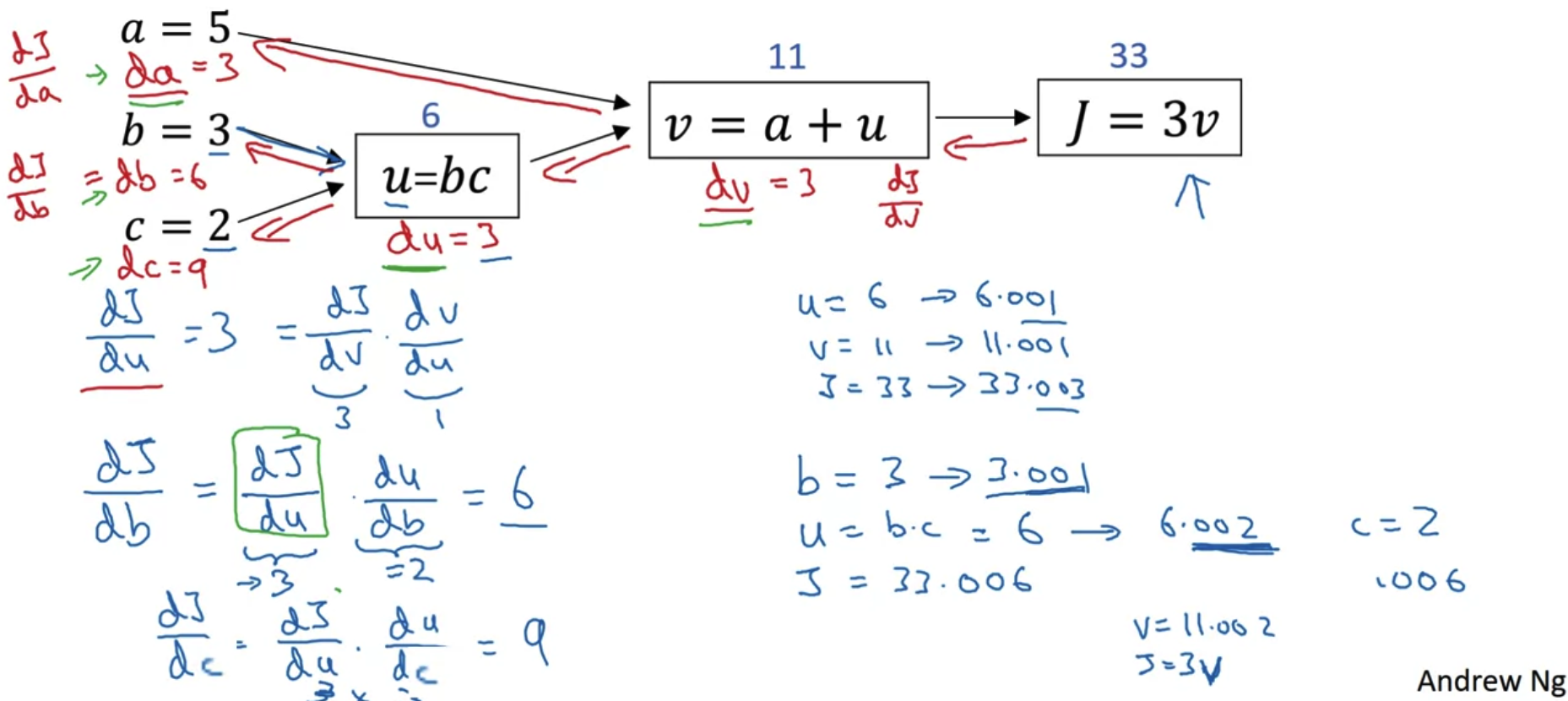
- right to left
- back-propagation
- 두 변수에 영향을 받는 u = bc 같은 경우도 b,c 각각 편미분하여 derivative를 구할 수 있다.
3. Derivatives with a Computation Graph
Logistic regression recap
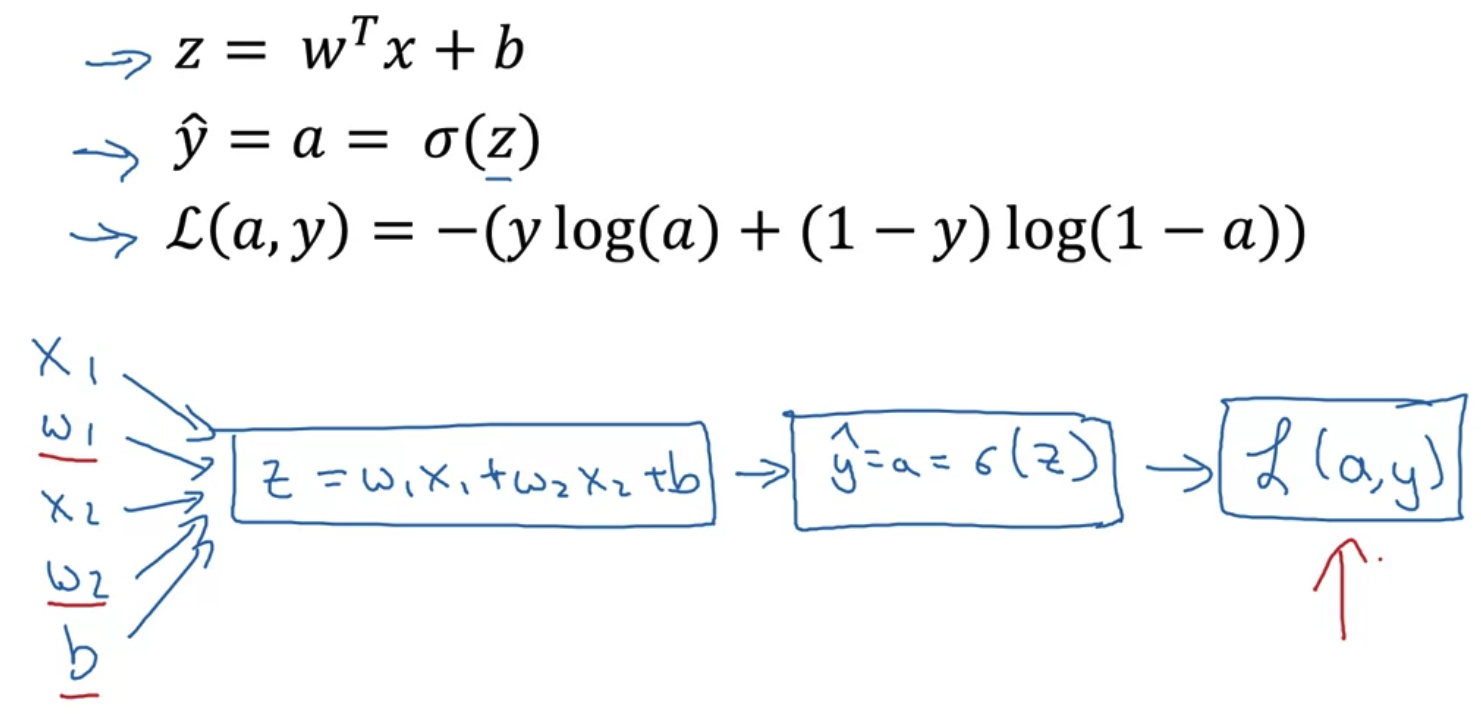
- 입력이 x1,x2개라면 위처럼 가중치와 곱하고 편향을 더한 것이 변수 z로 정의된다.
- 여기에 시그모이드 함수를 적용하면 y hat(추정치)이 된다.
- 이를 비교 대상 y(label)과의 차를 구한 것이 loss인 L로 정의되고 우리의 목표는 이를 최소화하는 w,b 를 찾는 것이다.
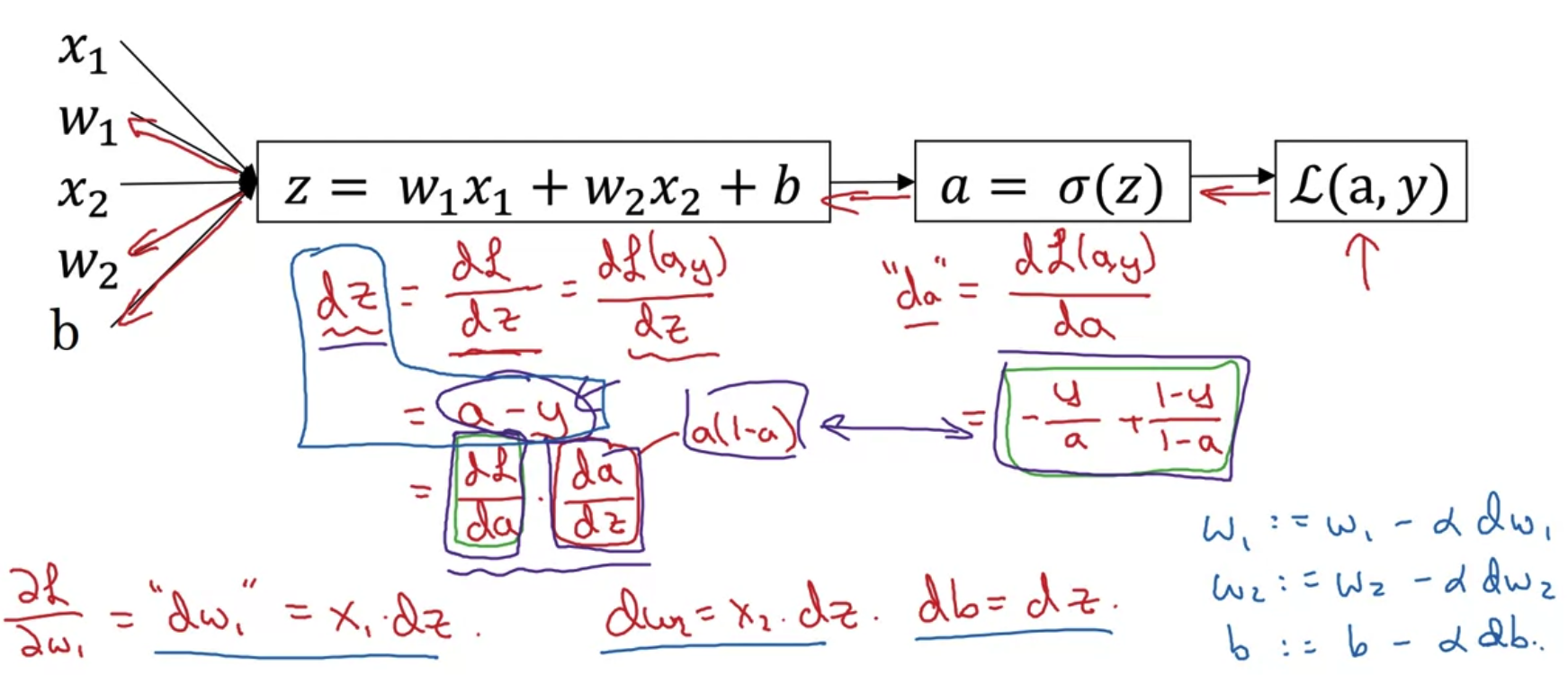
- loss를 최소화하는 w,b를 구하기 위해 연속적으로 chain rule을 수행하는 과정이다.
- 여기서 L을 a에 대해 미분할 때 필요한 log 미분에 대한 지식이나
a를 z에 대해 미분할 때 필요한 시그모이드 함수 미분에 대한 지식이 부족하더라도 결과만 이용할 수 있으면 된다. - sigmoid 미분에 대한 참고 사이트 주소
https://towardsdatascience.com/derivative-of-the-sigmoid-function-536880cf918e
Derivative of the Sigmoid function
In this article, we will see the complete derivation of the Sigmoid function as used in Artificial Intelligence Applications.
towardsdatascience.com
4. Gradient Descent on m Examples
Logistic regression on m examples
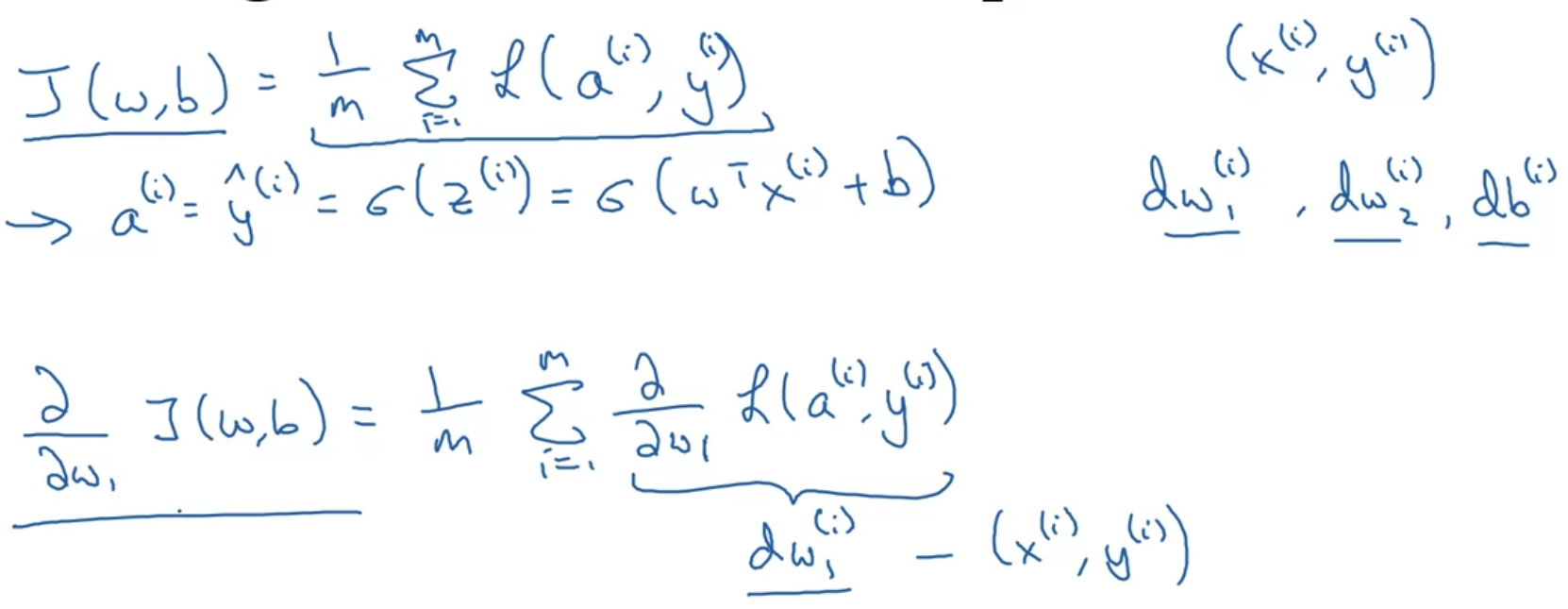
- 지금까지 공부한 Gradient Descent에 사용되는 변수들의 정의를 정리한 것이다.

- 위 변수들을 이용하여 실제로 gradient descent가 프로그램으로 구현되기 위한 방식을 정리한 것이다.
- logistic regression에 gradient descent를 적용하기 위한 방식으로 이해하면 된다.
- 단, 여기서는 for loop이 i = 1 to m 과 dz,dw,db에 대해 각각 적용된다는 문제점을 가진다.
dataset이 커질수록 for loop을 사용하는 방식을 유지하기 어려워지므로 이를 해결하기 위한 방식으로 vectorization을 이용할 것이다.
출처: Coursera, Neural Networks and Deep Learning, DeepLearning.AI
'Neural Networks and Deep Learning > 2주차' 카테고리의 다른 글
| Programming Assignments (2) | 2022.10.03 |
|---|---|
| Python and Vectorization(2) (0) | 2022.10.03 |
| Python and Vectorization(1) (0) | 2022.10.03 |
| Logistic Regression as a Neural Network(1) (0) | 2022.10.02 |
