![]()
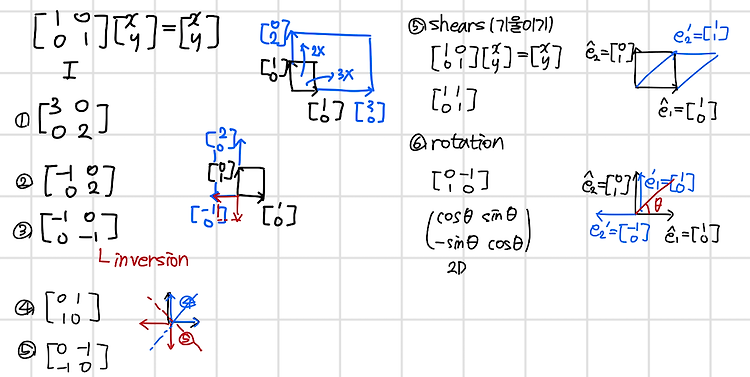
1. How matrices transform space 행렬의 곱을 단위벡터와의 곱으로 변환할 수 있다. 이때 분배법칙을 이용한다. 2. Types of matrix transformation possible sorts of changes we can do with a matrix 3. Composition or combination of matrix transformations 행렬의 곱은 순서를 다르게 하면 동일한 결과가 보장되지 않는다.(isn't commutative, 교환 법칙 x) 하지만 결합 법칙은 성립할 수 있다.(associative) 행렬의 곱은 변환에 변환을 적용한 것으로 이해할 수 있다. 4. Using matrices to make transformations(Quiz 6) 행렬..
![]()
1. Changing basis Coordinate System(좌표계) 벡터는 기저 벡터의 합으로 표현된다. 이 벡터를 다른 기저 벡터의 합으로 표현할 수 있다. 단, 이 기저 벡터들은 서로 직교해야 한다(orthogonal to each other) 직교하는 vector에 대해 내적(dot product) 취해보기 기저벡터 e1, e2로 벡터 r을 표현 또다른 기저벡터 b1,b2 scalar projection을 구하고 여기에 b1, b2의 방향벡터를 곱해서 vector projection을 구한다. 벡터 r이 기저벡터 b1, b2로 표현되는 것을 확인했다. 요약 vector는 우리가 지금 표현하는 axes에 묶여있는 것이 아니다. basis vector는 data의 공간을 표현한다. 위처럼 어떤 벡..
![]()
1. Modulus & inner product 벡터를 단위벡터로 표현하기 벡터는 length(길이)와 direction(방향)을 가진다. 단위벡터 i,j 로 벡터 r을 표현할 수 있다. i 와 j 의 상수배를 제곱하고 루트를 씌우면 r의 크기(길이)가 된다. 이는 피타고라스 정리에 의한 것이다. Inner(dot) product 정의하기(내적) 내적은 inner product, dot product, scalar product, projection product 등 다양하게 불린다. 두 벡터 r, s 가 있을 때 innder product는 다음과 같이 정의된다. 결과값은 벡터가 아닌 스칼라다. 벡터의 성질 세 가지 1) commutative (교환법칙 성립) 2) distribute over add..