1. Neural Networks Overview
What is a Neural Network?

- 앞선 강의들에서 배운 내용을 정리한 것이다.
입력 x를 가중치 w와 곱하고 편향 b를 더한 것을 z로 정의한다.
이 z에 시그모이드 함수를 적용하면 output이 된다. - 만약 layer가 깊어지면 z가 새로운 입력이 되어 새로운 가중치 및 편향과 계산을 하게 된다.
변수의 우측 상단에 적힌 [ ] 안의 숫자는 몇 번째 layer에 속하는지를 나타내고 있다. - 빨간색 화살표는 back-propagation을 뜻한다.
2. Neural Network Representation

- hidden layer: 어떤식으로 학습이 이루어지는지 우리가 직접 볼 수 없는 layer다.
- logistic regression에서는 a가 곧 y hat이 되었지만(여러 개의 layer가 없기 때문에),
neural network에서는 layer가 여러 개 존재하기 때문에 위 구조에서는 a[2]가 y hat이 된다. - notational convention에 따라 input layer는 layer로 count하지 않는다.
따라서 위 예시는 2 layer neural network가 된다. - 가중치 벡터의 size를 보면 '해당 layer의 노드 개수' x '이전 layer의 노드 개수'가 된다.
예를 들어 w[1]의 경우 wx의 결과가 hidden layer에서 네 개의 노드로 나타나므로 행이 네 개여야한다.
그리고 이는 input layer의 입력 x1,x2,x3 세 개를 받아 처리하는 것이므로 열은 세 개가 된다.
결과적으로 w[1] = 4 x 3 size 벡터가 되고, b[1] = 4 x 1 size 벡터가 된다.
3. Computing a Neural Network's Output

- 좌측은 logistic regresion을, 우측은 neural network를 도식화한 것이다.
- neural network에서 hidden layer의 node는 두 가지 단계로 나뉜다.
입력을 가중치 및 편향 벡터와 계산하여 z를 구하는 단계.
그리고 이 z를 활성화 함수 sigmoid에 넣어 변수 a로 만드는 단계. - 각 노드의 위첨자는 layer의 번호를, 아래첨자는 layer에서 몇 번째 node인지를 나타낸다.

- neural network는 결국 여러 개의 logistic regression을 수행하는 것과 동일하다.
하지만 동일한 방식의 계산을 여러 번 나눠서 하는 것은 비효율적이므로 이를 한꺼번에 처리하기 위해 vectorize한다.
쉽게 말하면 위에 정리된 네 개의 방정식을 하나의 세로로 쌓아 하나의 matrix로 만들어 한 번에 계산하는 것이다.

- 각 벡터의 size를 잘 살펴보는 것이 중요하다.
가중치 벡터 w를 matrix로 쌓기 전에는 계산을 위해 w.T 를 이용했다(행렬 곱 사이즈를 맞춰주기 위해).
하지만 이 벡터 w들을 세로로 쌓아서 만든 행렬 W는 transpose를 취할 필요가 없다.(이미 transpose된 벡터들로 만든 행렬이므로)
4. Vectorizing Across Multiple Examples

- Neural Network에서 각 변수들을 계산하는 과정은 하나의 example에 대해 적용되는 것이다.
이제는 여러 개의 example이 존재할 때의 계산을 vectorize하고자 한다.
벡터화하여 행렬로 계산하면 for-loop를 사용하지 않고도 한 번에 계산 가능하다. - 변수의 두 번째 위첨자가 몇 번째 example인지 나타내주고 있다.

- vectorize하는 과정은 위와 같다.
대문자 X,Z,A는 column vector로 구성된 matrix이다. - 각 행렬의 행과 열의 의미를 보면, 행(세로)은 hidden layer units의 개수를 열(가로)은 train examples의 개수를 뜻한다.
이는 각 example을 horizontally(가로로) 쌓아 matrix로 만들었기 때문이다.
5. Explanation for Vectorized Implementation
Justification for vectorized implementation
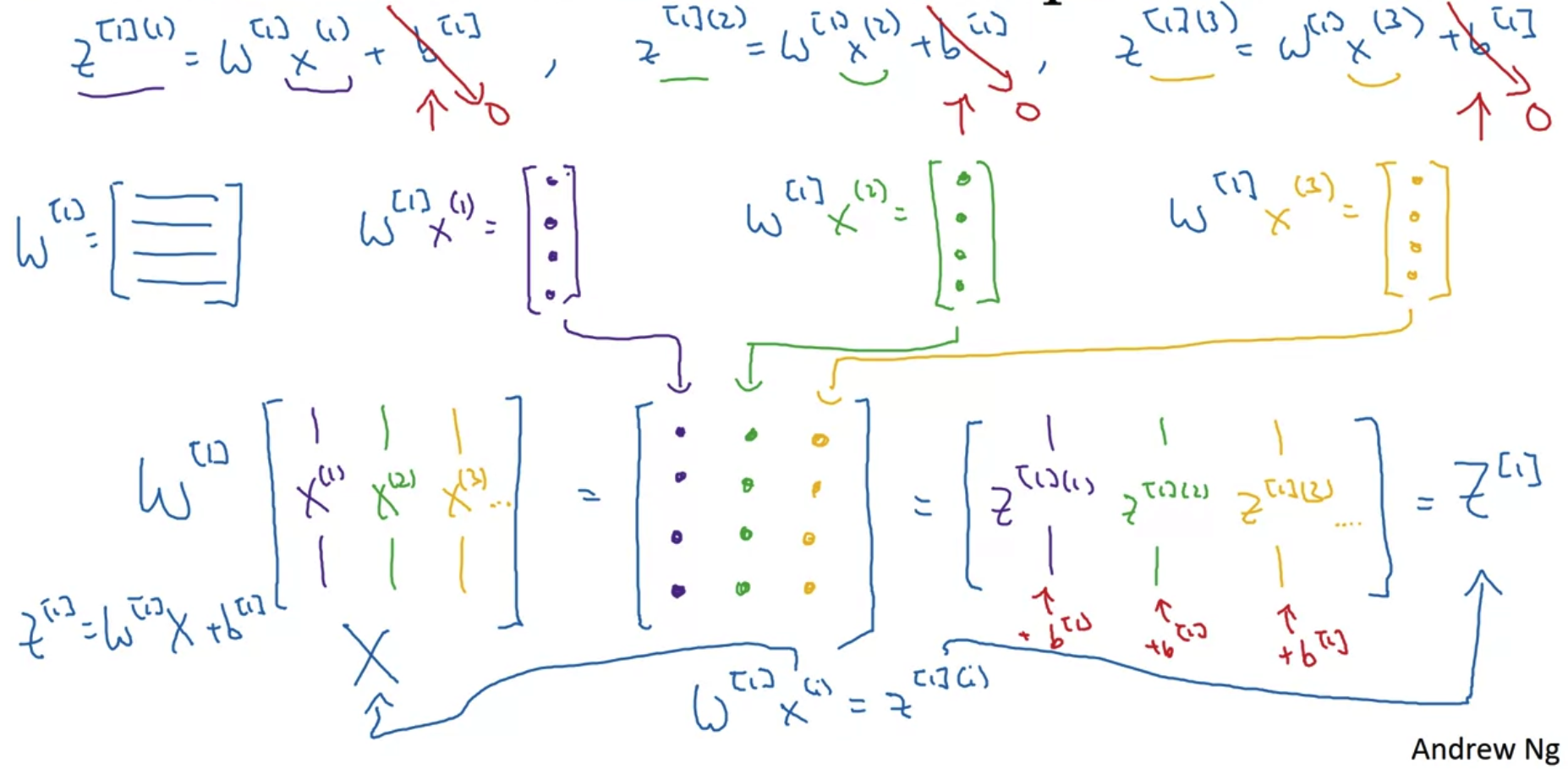
- vectorization을 justification하는 과정은 위와 같다.
- matrix w와 example x1,x2,x3를 계산한 결과를 matrix로 한꺼번에 묶어서 표현할 수 있다.
이때의 결과는 z가 되므로 z가 horizontally 묶인 matrix는 대문자 Z로 정의된다.
Recap of vectorizing across multiple examples

- 이전 슬라이드에서 살펴본 vectorization은 for문의 첫 번째 줄에 해당하는 식에 대한 것이었다.
해당 식을 vectorization 하는 것이 정당함이 밝혀졌으므로 나머지 명령에 대해서도 같은 방식을 적용할 수 있다.
출처: Coursera, Neural Networks and Deep Learning, DeepLearning.AI
'Neural Networks and Deep Learning > 3주차' 카테고리의 다른 글
| Quiz & Programming Assignment (0) | 2022.10.08 |
|---|---|
| Shallow Neural Network(3) (1) | 2022.10.08 |
| Shallow Neural Network(2) (1) | 2022.10.08 |
