1. Activation Functions
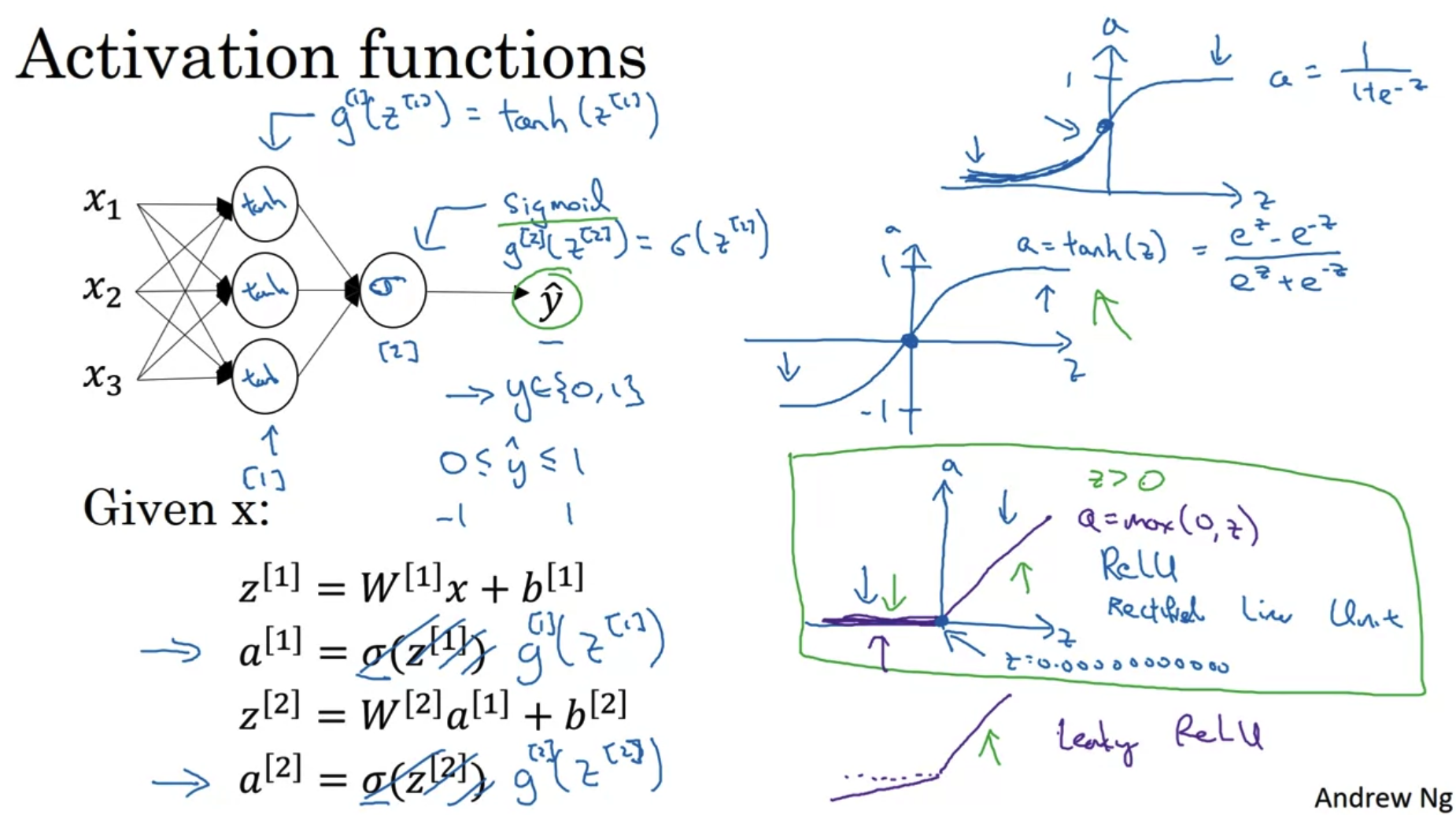
- 이제는 activation function으로 sigmoid를 사용하지 않는다.
거의 모든 경우에 대해서 tan h를 activation function으로 사용하는 것이 더 좋기 때문이다.
tan h는 sigmoid와 달리 non-linear한 내용에도 적용될 수 있다.
- 단, output layer의 activation function으로 sigmoid를 사용하는 것이 tan h를 사용하는 것보다 편리한 경우가 예외로 존재한다.
이때는 y(label)이 0 또는 1로 구분되는 이진분류인 경우인데, y hat의 범위가 -1에서 1인 것보다 0에서 1로 나오는 것이 더 좋기 때문이다. - 따라서 hidden layer의 activation function은 sigmoid 대신 tan h를 사용하는 것이 좋고,
이진분류를 하는 경우 output layer의 activation function으로는 sigmoid를 사용하는 것이 좋다.
- 단, output layer의 activation function으로 sigmoid를 사용하는 것이 tan h를 사용하는 것보다 편리한 경우가 예외로 존재한다.
- ReLU(Rectified Linear Unit)
- sigmoid나 tanh는 z의 값이 크거나 작을 때 그 derivative가 0으로 수렴한다.
따라서 학습이 진행되는 속도가 느리다. - 하지만 ReLU는 z가 양수인 경우 그 미분계수가 항상 1이므로 학습속도가 월등히 빠르다.
- z가 0인 경우 아주 약한 경사를 이루는 leaky ReLU도 존재하지만 교수님은 주로 ReLU를 사용한다고 하셨다.
- sigmoid나 tanh는 z의 값이 크거나 작을 때 그 derivative가 0으로 수렴한다.
Pros and cons of activation functions

- 위에서 언급된 네 종류의 activation functions 그래프는 이처럼 그려진다.
- sigmoid는 이진분류를 하는 경우 output layer에만 사용된다.
- tanh는 대부분의 경우 hidden layer에서 sigmoid보다 훨씬 좋은 성능을 발휘한다.
- 하지만 일반적으로 ReLU의 성능을 따라잡을 수는 없으므로 거의 ReLU가 사용된다.
심지어 이를 개선한 Leaky ReLU가 있음에도 ReLU를 사용한다.
2. Why do you need Non-Linear Activation Functions?
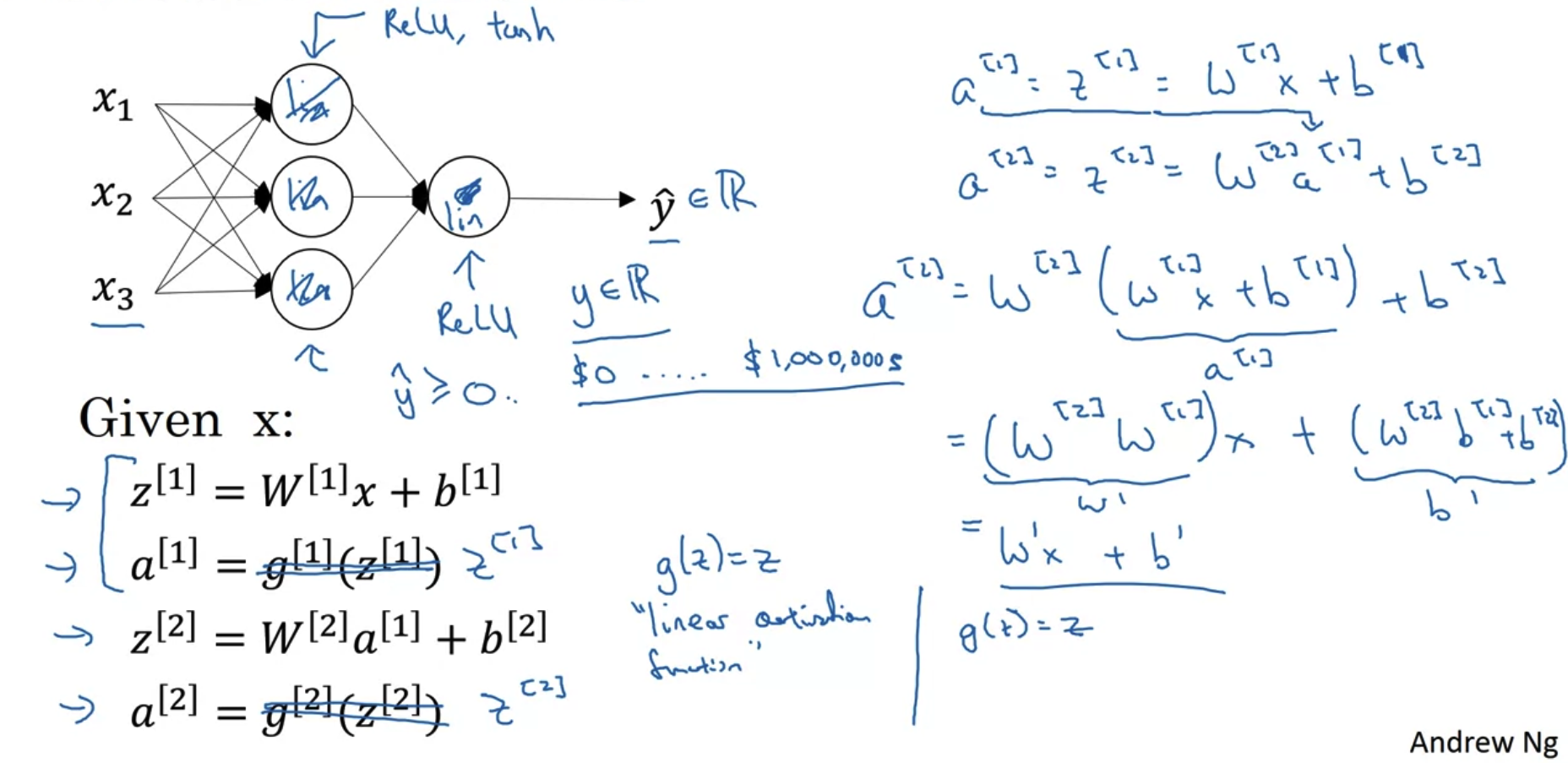
- linear activation function인 sigmoid를 사용하는 경우,
그 계산 결과는 항상 linear하게 표현된다.
즉, 아무리 hidden layer를 많이 쌓아 deep한 neural network를 만들더라도,
단순히 한 층만 쌓는 Linear Regression 문제와 다를 것이 없는 것이다. - 따라서 우리는 아주 특수한 경우를 제외하고서는 neural network를 구성하는데에 linear activation function을 쓰지 않는다.
- 예를 들어 집값과 같이 y hat(계산을 통해 나온 y의 추정치)의 범위가 실수인 경우,
이때는 출력층의 활성화함수로 선형함수를 사용할 수 있다. - 그 외에는 compression과 같은 이유로 hidden layer에 사용되는 경우가 있다고 하지만 extremely rare한 케이스라고 한다.
- 예를 들어 집값과 같이 y hat(계산을 통해 나온 y의 추정치)의 범위가 실수인 경우,
3. Derivatives of Activation Functions
Sigmoid activation function
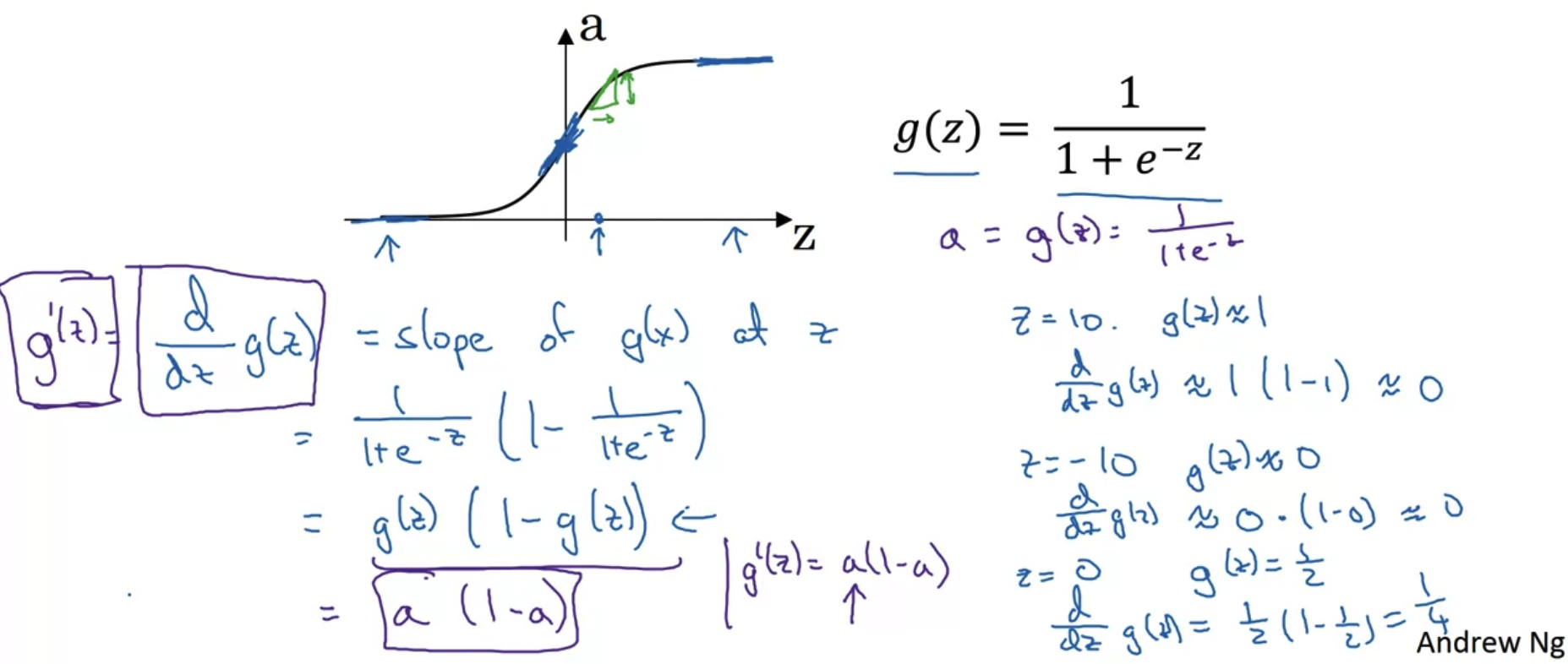
- sigmoid function은 z의 값이 크거나 작으면 그 미분계수가 0에 수렴한다.
- 시그모이드를 미분하는 과정이 어떻게 되는지는 개인적으로(선택적으로) 학습하면 된다.
우리는 그 결과를 이용하여 g(z) = a 라고 정의했을 때, g'(z) = a(1-a)라고 표현할 수 있다.
이는 코드로 구현할 때 자주 사용되는 표현이니 기억해두도록 하자.
Tanh activation function
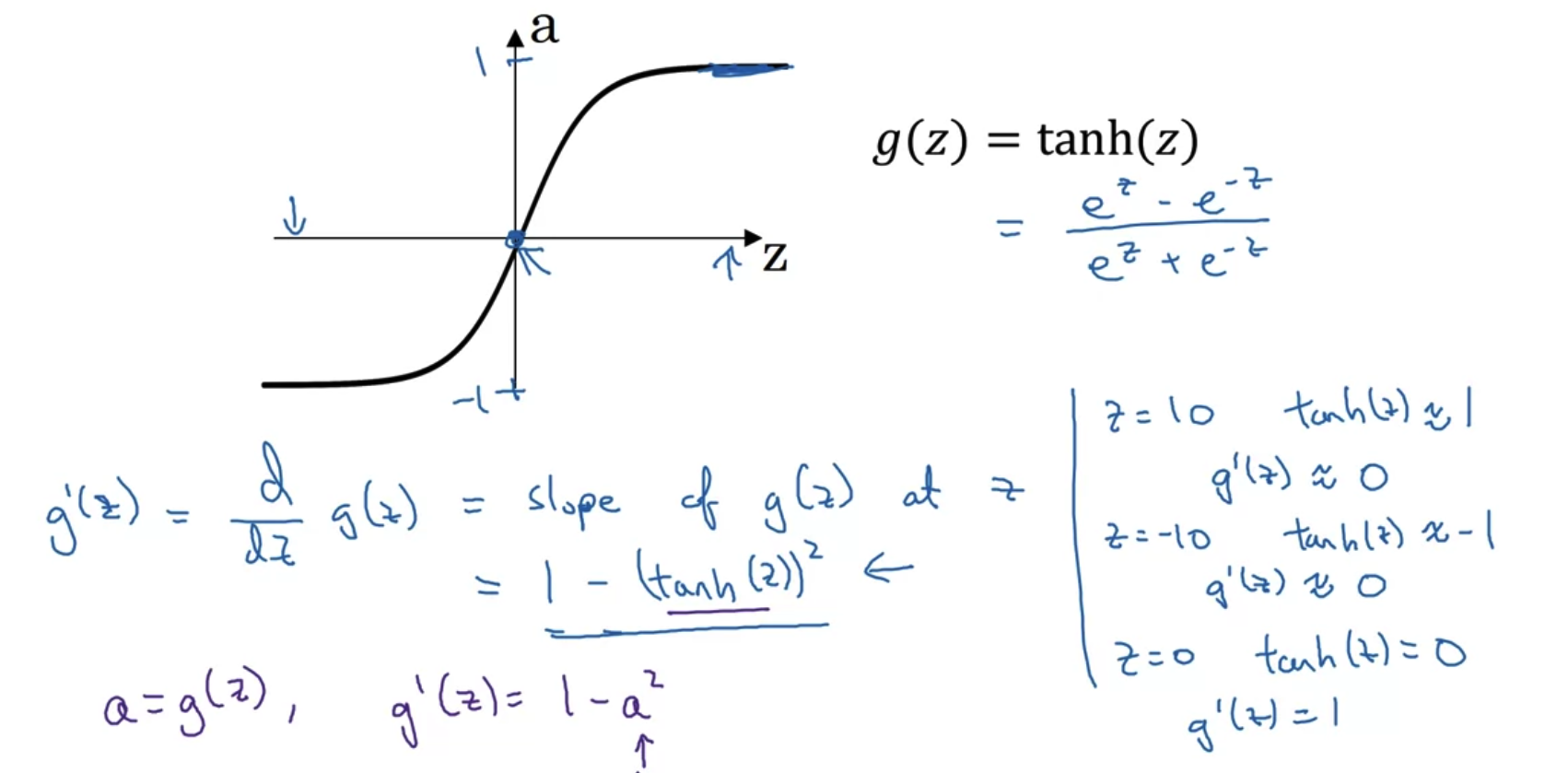
- tanh function도 마찬가지로 z의 값이 크거나 작을 때는 그 미분계수가 0에 수렴한다.
- tanh에 대한 미분 결과는 1 - (tanh(z))^2 임을 기억하도록 하자.
ReLU and Leaky ReLU
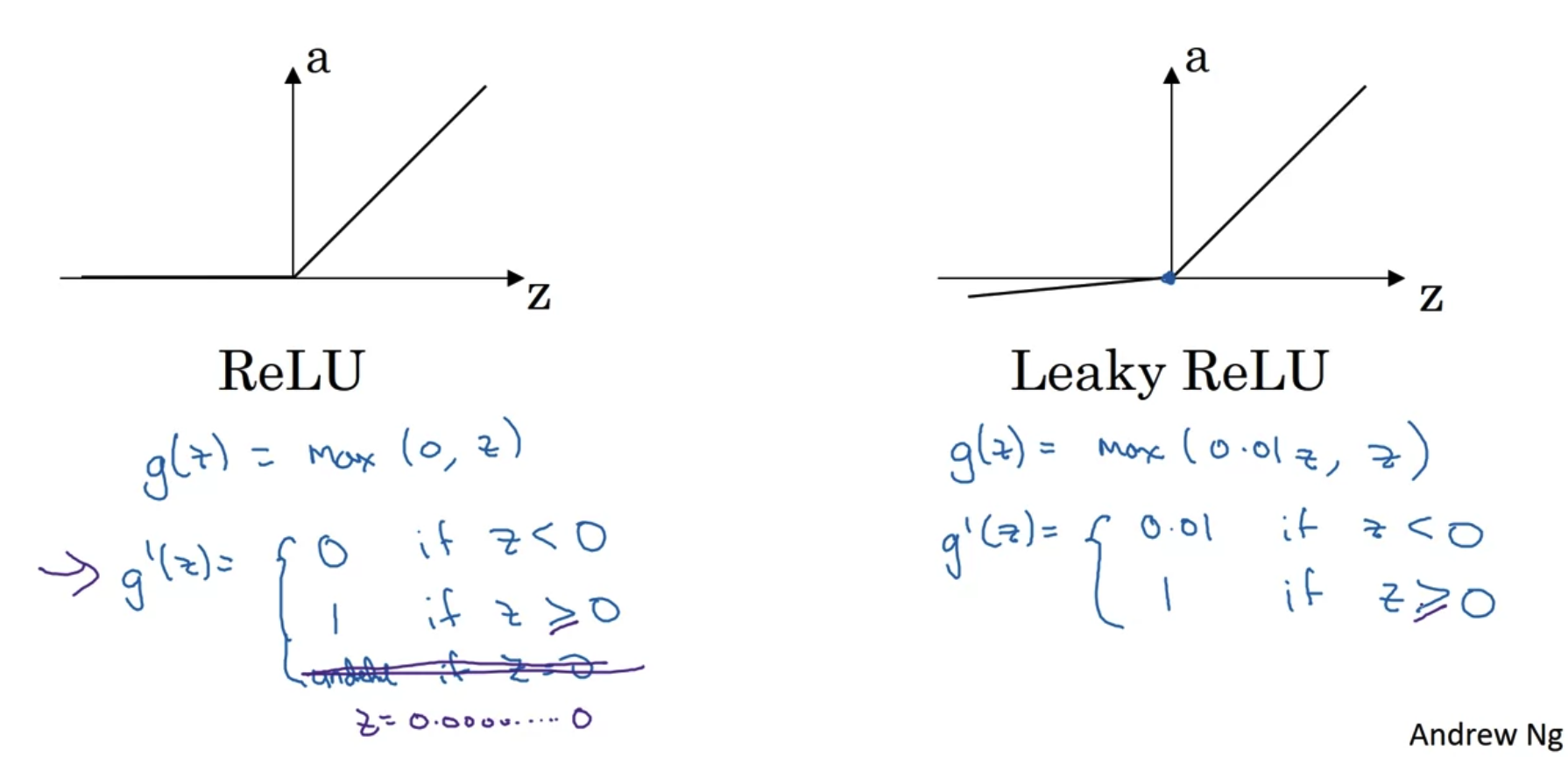
- ReLU는 0을 기준으로 그 미분계수가 달라진다.
Leaky ReLU는 z < 0일 때 그 미분계수가 0.01로 정의되어있다. - z = 0은 정확히 정의될 수 없다.
컴퓨터에게 수학적인 0은 정의되지 않기 때문에 0.0000000와 같은 굉장히 작은 숫자로 처리된다.
그렇다고 하더라도 우리가 원하는 결과를 얻어내기에는 아무런 문제가 없다.
출처: Coursera, Neural Networks and Deep Learning, DeepLearning.AI
'Neural Networks and Deep Learning > 3주차' 카테고리의 다른 글
| Quiz & Programming Assignment (0) | 2022.10.08 |
|---|---|
| Shallow Neural Network(3) (1) | 2022.10.08 |
| Shallow Neural Network(1) (1) | 2022.10.08 |
