목차
1. Normalizing Activation in a Network
Normalizing inputs to speed up learning
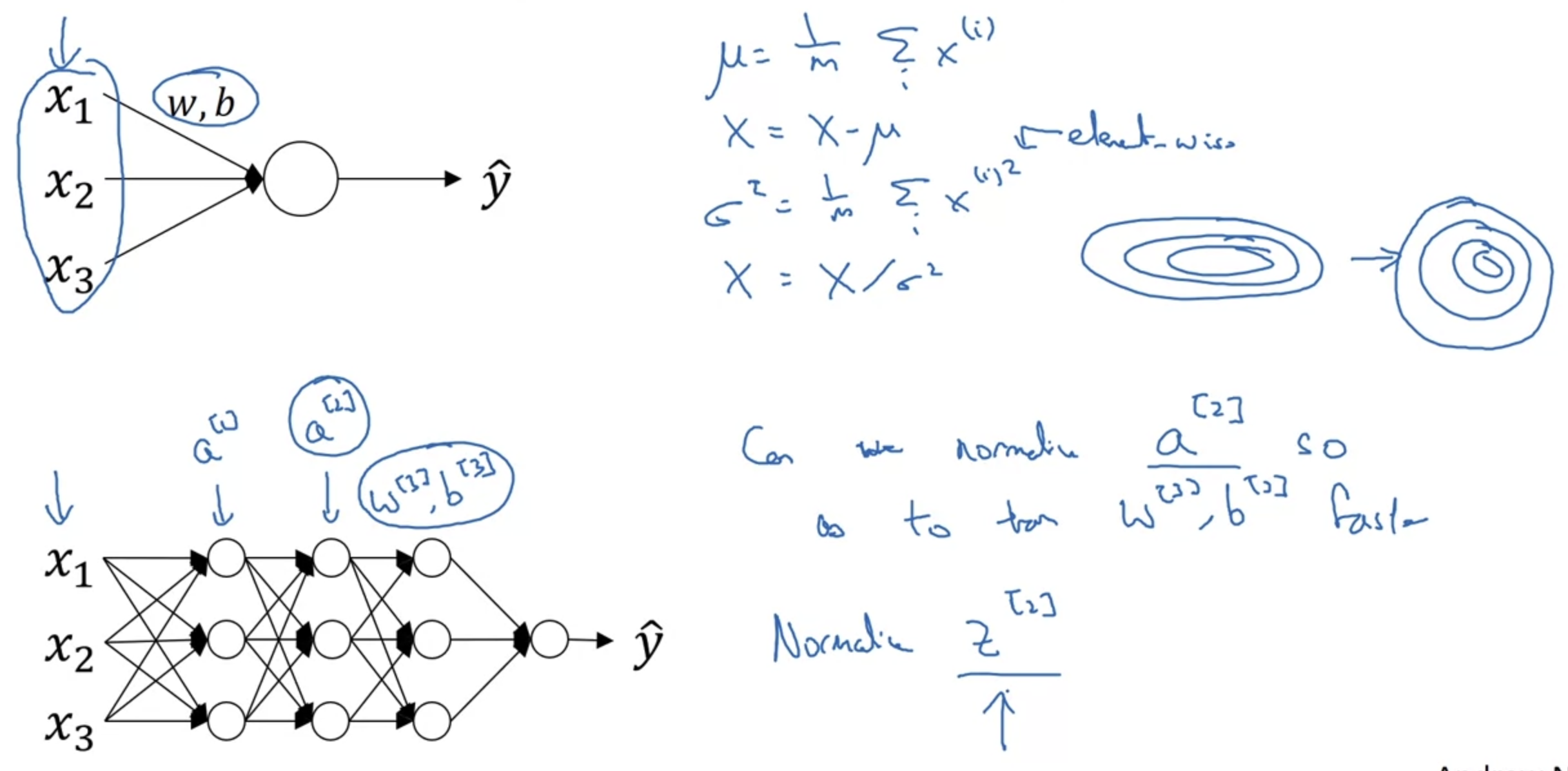
- gradient descent 과정에서 빠르게 local minima에 도달하는데 normalization이 도움이 된다는 것은 이전에 배웠다.
- 그렇다면 neural network에서, 즉 hidden layer가 여러 개인 경우에는 normalization을 언제언제 적용해야 할까?
- 다시 말하자면 input만 normalization을 해야할까? 아니면 activation function을 통해 나온 결과값에도 적용을 해야할까?
- 교수님은 둘 다 하는 것을 default로 생각하라고 하셨다.
activation function의 결과가 어떻게 나올지는 확실히 예측할 수 있는 것이 아니라서 매번 normalization을 적용하는 것이 안전하다라는 느낌으로 받아들였다
Implementing Batch Norm
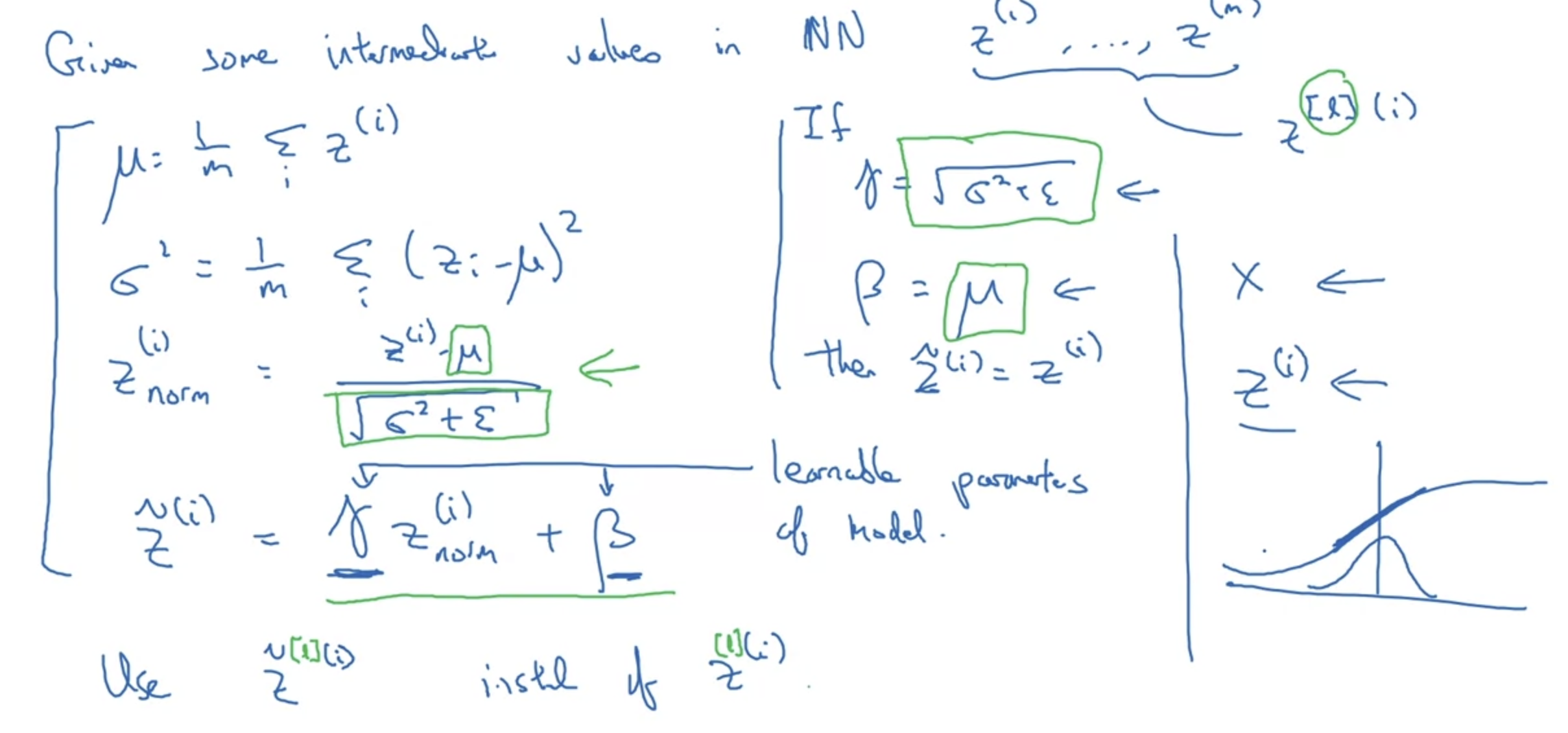
- 각 Batch에 대해 Normalization을 적용하는 것은 왼쪽의 네 개 수식을 통해서 가능하다.
평균, 분산, z(norm), z(i) 네 개의 식이다. - 하지만 위와 같은 normalization을 모든 변수에 대해 적용한다면 모든 변수가 '평균이 0, 분산이 1'인 분포를 가질 것이다.
이는 우리가 의도한 바가 아니다.
구체적인 예를 들면(오른쪽 sigmoid function 그림), 우리가 활성화 함수를 이용하는 이유는 비선형 근사를 하기 위함인데, x축에 해당하는 값이 y축 중심에 모여있게 된다면 활성화 함수를 사용한 의미를 상실하게 되는 것이다. - 이러한 문제를 해결해주는 것이 gamma와 beta라는 변수들이고, 이 둘은 step마다 update 되는 변수들이다.
z에 곱해지는 gamma와 여기에 더해지는 beta를 통해 각 변수들이 다양한 분포를 가질 수 있게 된다.
2. Fitting Batch Norm into a Nerual Network
Adding Batch Norm to a network
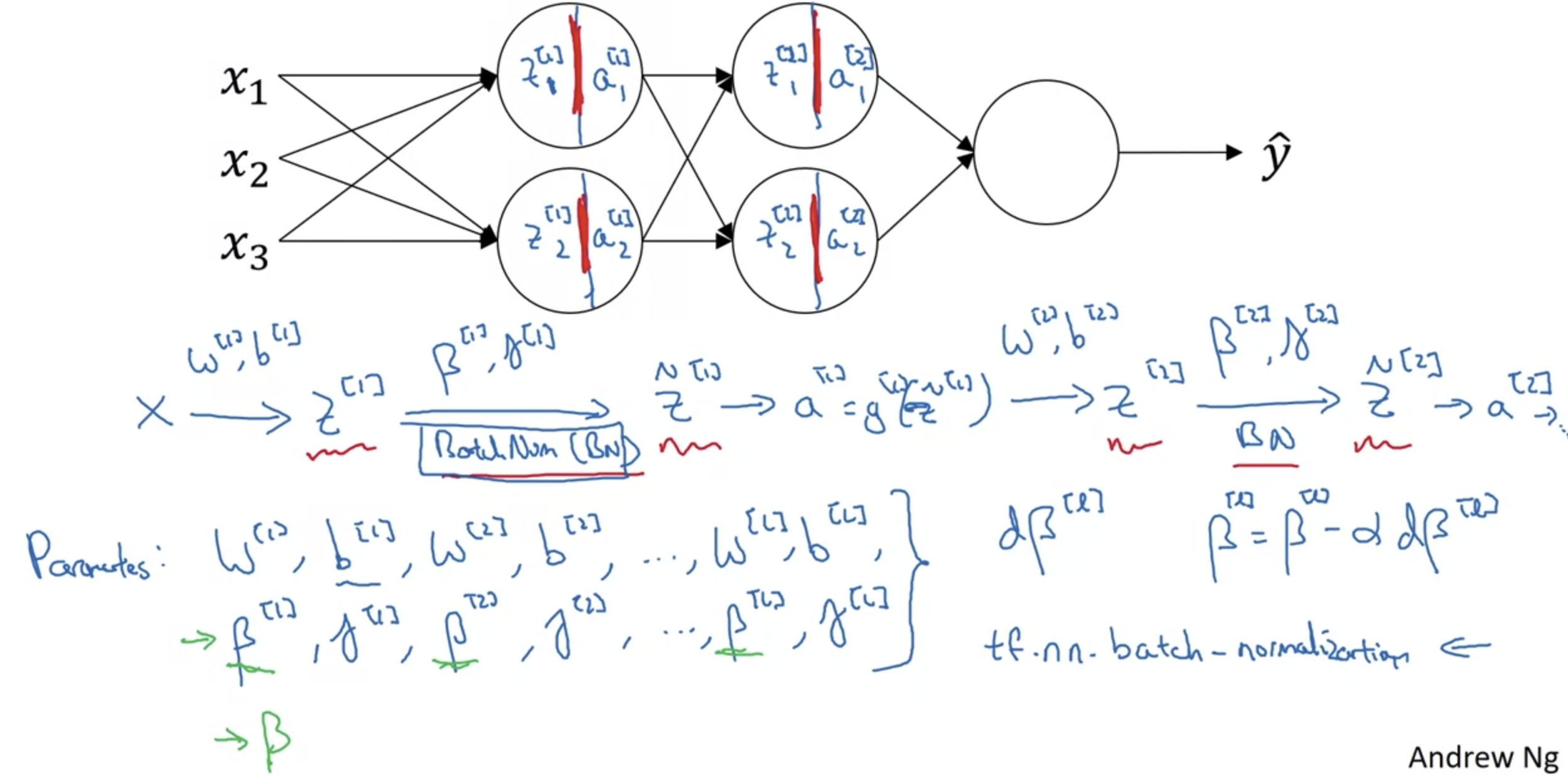
- Neural Network에 Normalization을 적용하는 과정을 도식화 한 것이다.
- 각 layer에서 W(eight)와 b(ias)를 이용하여 z를 계산하고, 이를 활성화함수 g의 변수로 사용하여 a를 구한다.
이때 z를 mean과 variance를 이용하여 normalization하고 여기에 gamma와 beta를 parameter로 추가할 수 있다. - 참고로 이때 쓰이는 beta라는 변수는 다른 optimization 함수, 예를 들어 RMS prop, AdamW 등에 사용되는 변수 beta와 완전히 다른 것이므로 헷갈리지 않도록 하자.
교수님께서는 각 논문에서 사용된 변수를 그대로 고수하겠다고 말씀하셨다.
Working with mini-batches
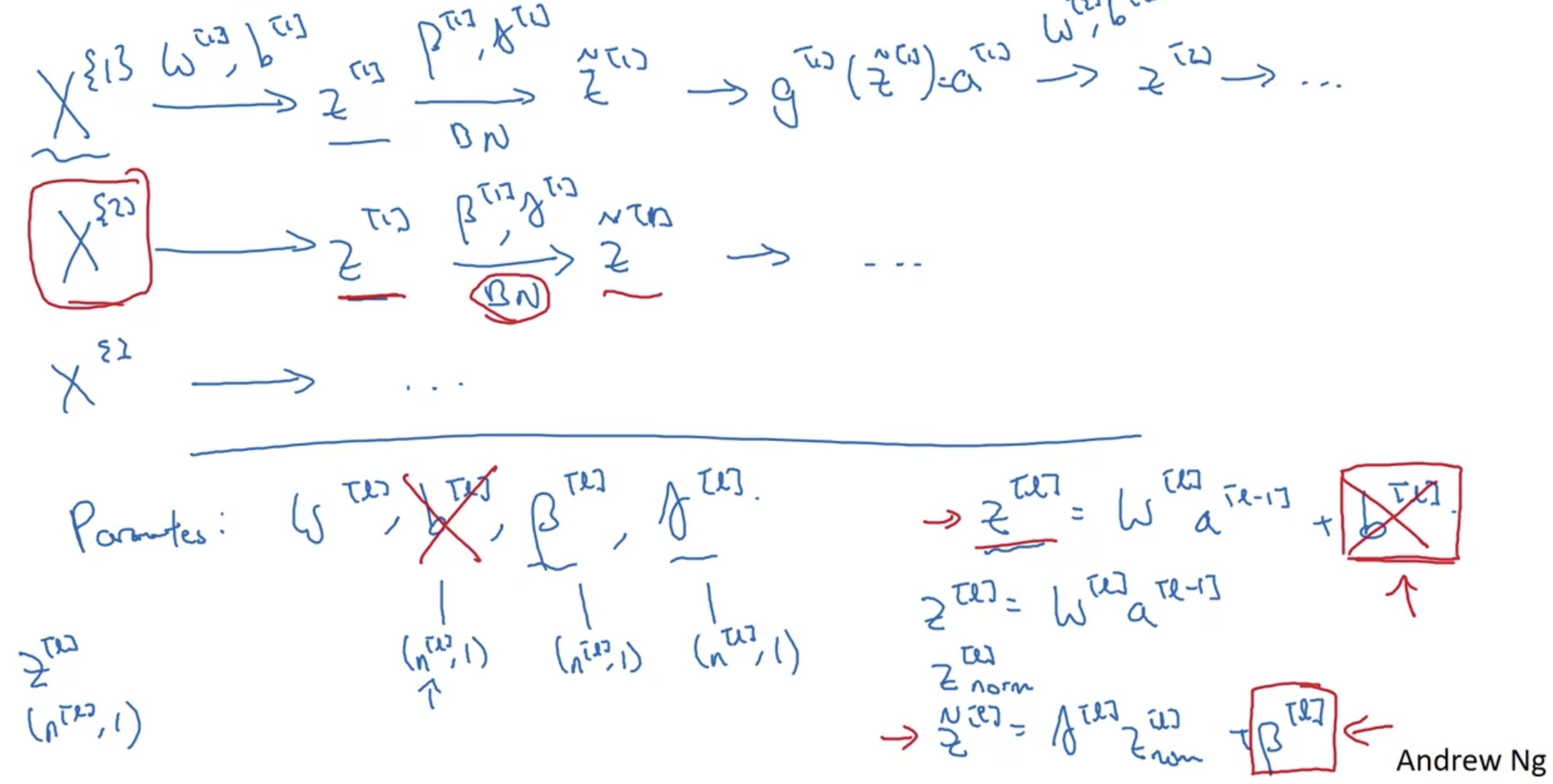
- 각 mini-batch에 대해서도 Batch Normalization을 적용할 수 있다.
이전과 마찬가지로 W와 b를 통해 구한 변수 z를 mean으로 빼고 variance로 나눠 normalization이 가능하다. - 결과적으로 연산에 영향을 주는 W,b,gamma,beta 변수 중에서 bias는 그 의미를 상실한다.
매 layer에서 모든 변수는 그 mean을 subtract(빼다)하기 때문이다. - 각 변수들이 갖는 차원의 크기를 생각해보면 W,b는 원래 (n[l], 1)이었고 gamma와 beta도 다르지 않다.
이때 n[l]은 각 layer가 갖는 hidden size이다.
mini-batch의 크기에 따라 나머지 차원도 변할 것이다.
Implementing gradient descent
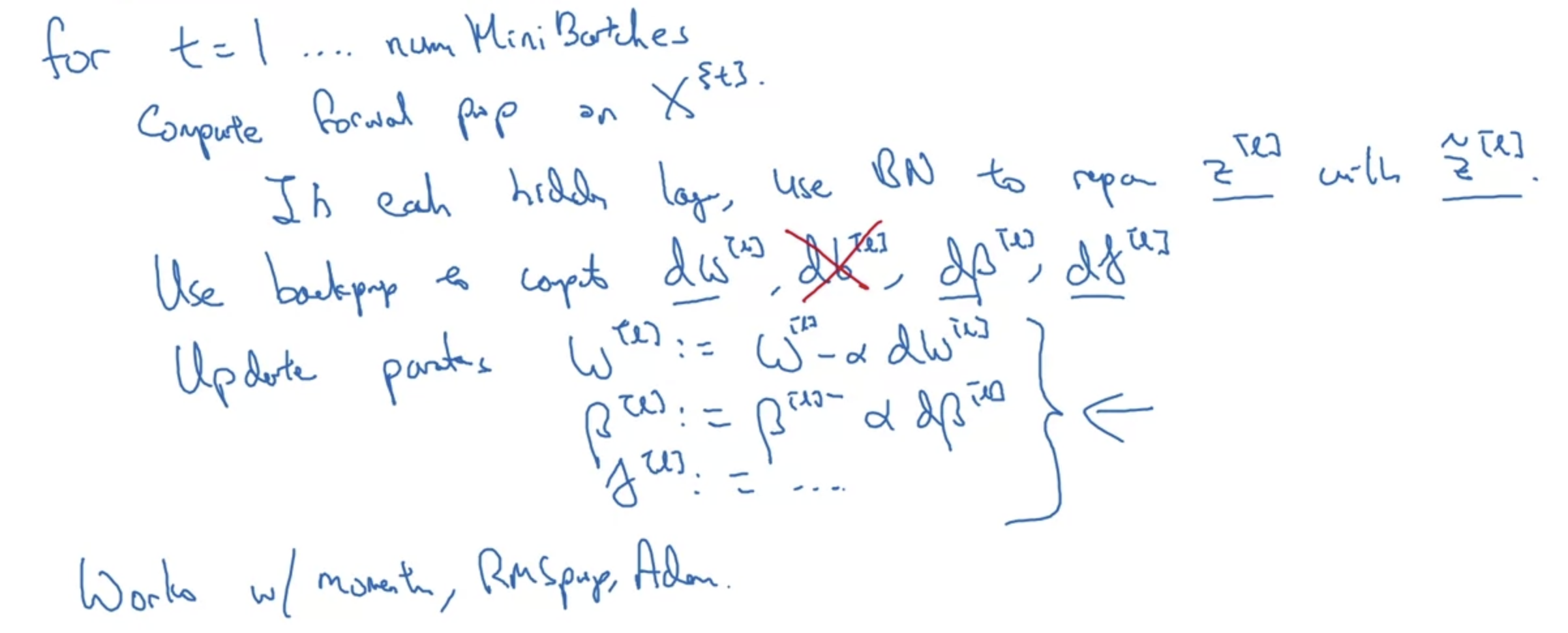
- 지금까지 공부한 Batch Normalization을 코드로 구현하면 위와 같은 모양이 될 것이다.
- 우선 forward하고 각 z에 대해 normalization을 적용한 뒤, backpropagation을 통해 W, gamma, beta를 update할 것이다.
- 여기서 backpropagation을 통해 세 변수를 업데이트하는 것은 이전에 공부한 optimizer인 Adam, RMSprop 등을 적용하는 것과 같은 역할을 한다.
따라서 위 방식 대신 다른 optimizer들을 사용하는 것도 방법이 될 수 있다는 것이다.
3. Why does Batch Norm work?
Learning on shifting input distribution
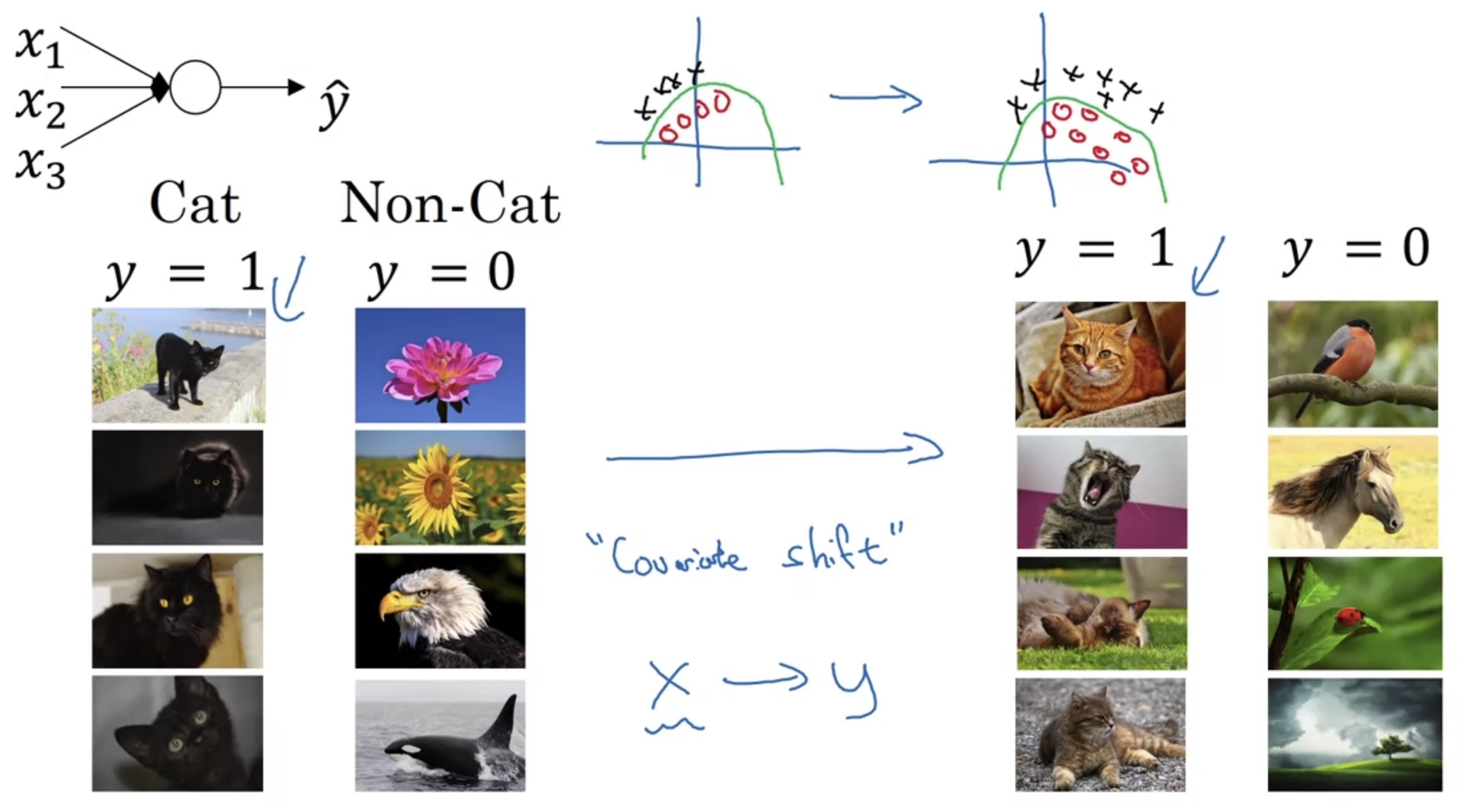
- 모델이 고양이인지 아닌지를 판별하는 학습을 하는 상황을 가정하자.
만약 왼쪽처럼 검은색 고양이에 대해서만 학습을 하게 된다면, 다양한 색의 고양이들에 대해서는 정확한 예측이 어려울 것이다. - 다시 말하자면 지금 학습하는 것이 잘 하고 있는 것처럼 보이더라도, 실제로는 굉장히 편향된 학습일 수 있다는 것이다.
- 이처럼 X와 Y를 mapping하는 문제에서 변수가 통째로 이동하는 것을 Covariate(공변량) Shift라고 하는데, 이 문제를 해결할 방법을 떠올려 보아야 한다.
Why this is a problem with neural networks?

- 이전에 비해 조금 더 복잡한 구조의 Neural Network가 존재한다고 가정해보자.
세 번째 혹은 네 번째 layer에 해당하는 변수들은 이전 layer들에 존재하는 변수들에 영향을 받을 것이다.
왜냐하면 각 layer에 입력으로 주어지는 변수 a는 이전 layer에서의 변수들로 계산되기 때문이다. - Normalization은 mean(평균)과 variance(분산)를 특정 값으로 고정시켜주기 때문에 이전 layer에서의 변수들로부터의 영향을 줄여준다.
다르게 말하자면 복잡한 구조를 가진 Network일수록 이전 layer에서의 Covariate Shift라는 문제점이 심각해질 수 있는데 이를 예방할 수 있다는 것이다.
Batch Norm as regularization

- Batch Norm은 우리가 의도했던 바와 달리 side effect(부작용)를 가질 수 있다.
Dropout 기법처럼 regularization의 효과를 가질 수 있다는 것이다. - 본래 Normalization은 변수들의 값을 조정하여 연산의 속도를 줄여주는 등의 효과를 가지는데, Batch Norm을 적용함으로써 noise가 추가되는 효과 또한 발생한다.
왜냐하면 기존의 연산에 mean을 빼고 variance로 나누는 등의 행위를 하기 때문이다. - 따라서 mini-batch를 기준으로 학습을 한다면 각 mini-batch에 대해 noise가 추가되는데, 이는 모델이 다양한 경우에 대해 보다 robust해지는 결과로 이어지게 된다.
이를 예상치 못한 side effect로 볼 수 있는 것은 이 효과가 의도하지 않더라도 발생할 수 있기 때문이다.
따라서 필요하다면 Batch Norm을 Dropout과 함께 사용하거나 하나만 사용하거나 할 수 있다. - 한편 mini-batch의 크기가 크면 클수록 noise는 줄어든다.
따라서 Batch Norm의 의도치 않은 side effect를 줄이고 싶다면 mini-batch size를 키우는 방식도 고려해 볼 수 있다.
4. Batch Norm at Test Time
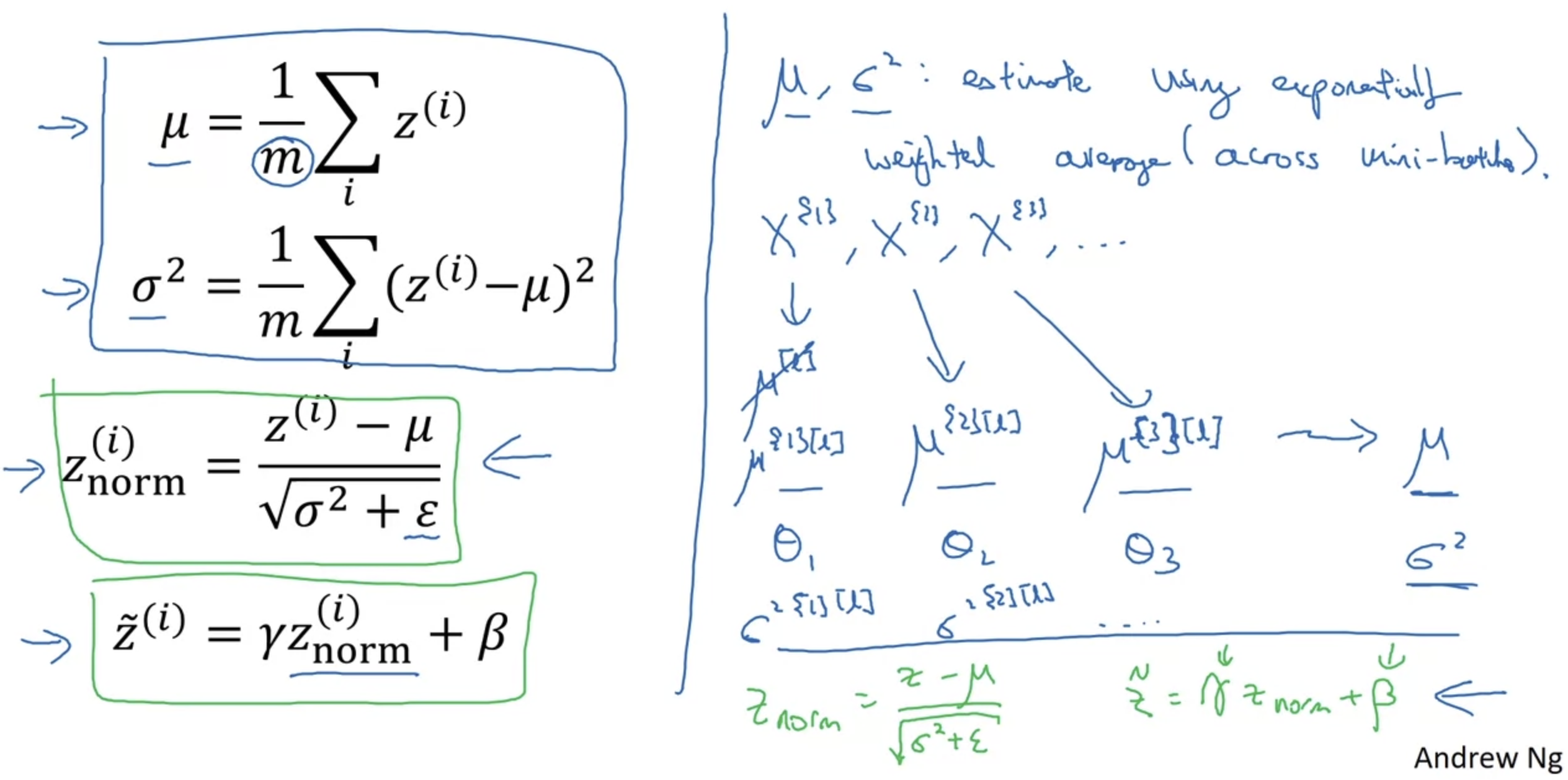
- 왼쪽은 평균, 분산, 표준화, scaling의 식이다.
- mini-batch를 사용하는 경우 mini-batch 간 exponentially weighted average를 사용할 수 있다.
- train 동안에는 mini-batch 단위로 학습이 이뤄지지만 test 할 때는 각 항목을 따로 확인해야 한다.
예를 들어 mini-batch가 64인 경우, test에서는 mini-batch가 1인 셈이다.
이런 경우 train에서의 mini-batch가 가지는 평균을 estimate하여 test에 적용해야 한다. - 이때 사용되는 평균이 exponentially weighted average인 것이다.
- Exponentially Weighted Average 관련 포스팅 : https://chanmuzi.tistory.com/133
Optimization Algorithms(2) - Exponentially Weighted Averages
1. Exponentially Weighted Averages (지수 가중 평균) Temperature in London 영국의 1년 날씨를 날짜에 따라 표시한 그래프다. 전날과 오늘의 관계를 수식적으로 표현하여 그래프가 그려지는 양상을 예측하고자
chanmuzi.tistory.com
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 3주차' 카테고리의 다른 글
| Quiz & Assignment (0) | 2022.12.30 |
|---|---|
| Introduction to Programming Frameworks (0) | 2022.12.30 |
| Multi-class Classification (0) | 2022.12.24 |
| Hyperparameter Tuning (0) | 2022.12.18 |
1. Normalizing Activation in a Network
Normalizing inputs to speed up learning

- gradient descent 과정에서 빠르게 local minima에 도달하는데 normalization이 도움이 된다는 것은 이전에 배웠다.
- 그렇다면 neural network에서, 즉 hidden layer가 여러 개인 경우에는 normalization을 언제언제 적용해야 할까?
- 다시 말하자면 input만 normalization을 해야할까? 아니면 activation function을 통해 나온 결과값에도 적용을 해야할까?
- 교수님은 둘 다 하는 것을 default로 생각하라고 하셨다.
activation function의 결과가 어떻게 나올지는 확실히 예측할 수 있는 것이 아니라서 매번 normalization을 적용하는 것이 안전하다라는 느낌으로 받아들였다
Implementing Batch Norm

- 각 Batch에 대해 Normalization을 적용하는 것은 왼쪽의 네 개 수식을 통해서 가능하다.
평균, 분산, z(norm), z(i) 네 개의 식이다. - 하지만 위와 같은 normalization을 모든 변수에 대해 적용한다면 모든 변수가 '평균이 0, 분산이 1'인 분포를 가질 것이다.
이는 우리가 의도한 바가 아니다.
구체적인 예를 들면(오른쪽 sigmoid function 그림), 우리가 활성화 함수를 이용하는 이유는 비선형 근사를 하기 위함인데, x축에 해당하는 값이 y축 중심에 모여있게 된다면 활성화 함수를 사용한 의미를 상실하게 되는 것이다. - 이러한 문제를 해결해주는 것이 gamma와 beta라는 변수들이고, 이 둘은 step마다 update 되는 변수들이다.
z에 곱해지는 gamma와 여기에 더해지는 beta를 통해 각 변수들이 다양한 분포를 가질 수 있게 된다.
2. Fitting Batch Norm into a Nerual Network
Adding Batch Norm to a network

- Neural Network에 Normalization을 적용하는 과정을 도식화 한 것이다.
- 각 layer에서 W(eight)와 b(ias)를 이용하여 z를 계산하고, 이를 활성화함수 g의 변수로 사용하여 a를 구한다.
이때 z를 mean과 variance를 이용하여 normalization하고 여기에 gamma와 beta를 parameter로 추가할 수 있다. - 참고로 이때 쓰이는 beta라는 변수는 다른 optimization 함수, 예를 들어 RMS prop, AdamW 등에 사용되는 변수 beta와 완전히 다른 것이므로 헷갈리지 않도록 하자.
교수님께서는 각 논문에서 사용된 변수를 그대로 고수하겠다고 말씀하셨다.
Working with mini-batches
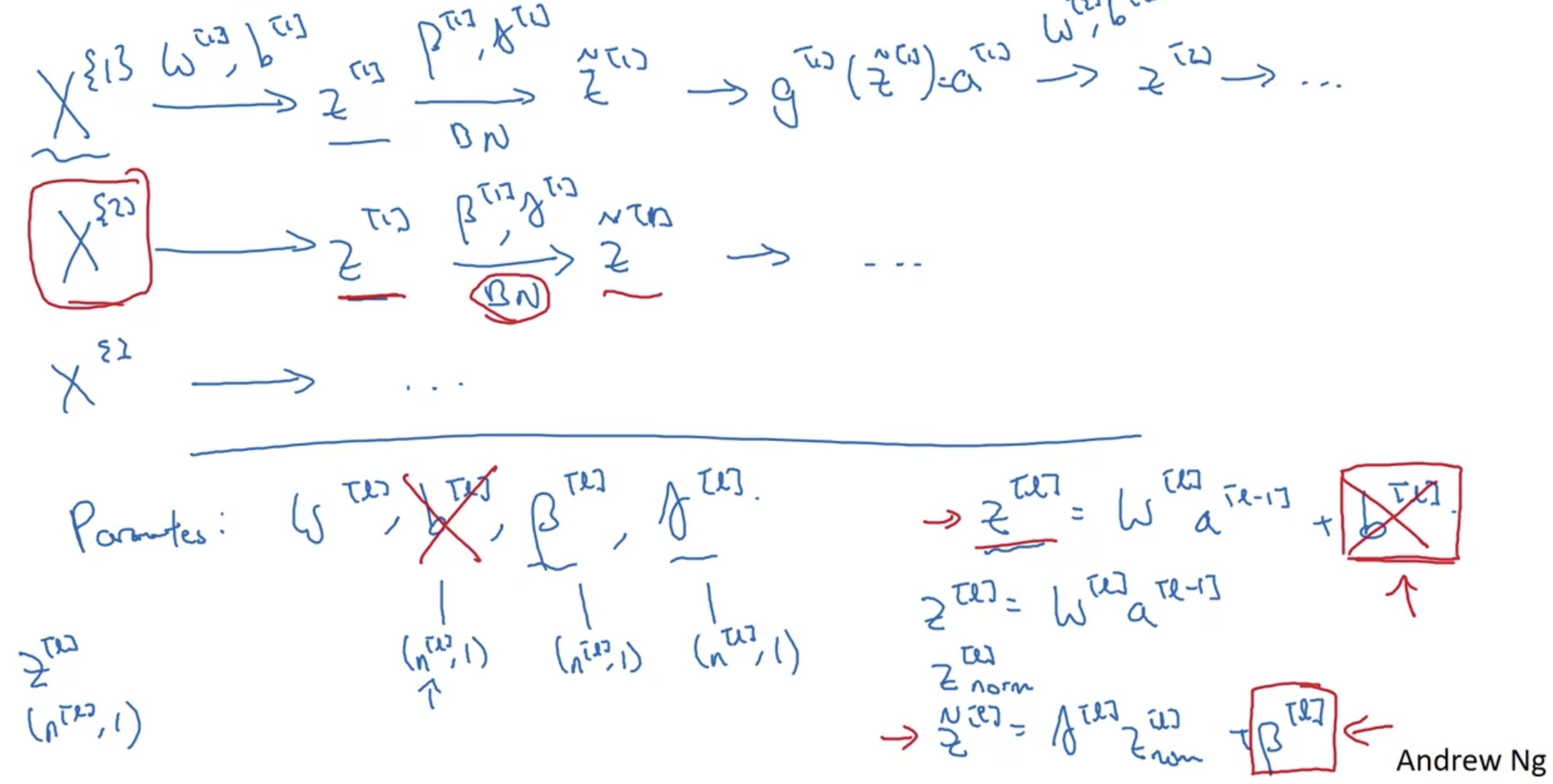
- 각 mini-batch에 대해서도 Batch Normalization을 적용할 수 있다.
이전과 마찬가지로 W와 b를 통해 구한 변수 z를 mean으로 빼고 variance로 나눠 normalization이 가능하다. - 결과적으로 연산에 영향을 주는 W,b,gamma,beta 변수 중에서 bias는 그 의미를 상실한다.
매 layer에서 모든 변수는 그 mean을 subtract(빼다)하기 때문이다. - 각 변수들이 갖는 차원의 크기를 생각해보면 W,b는 원래 (n[l], 1)이었고 gamma와 beta도 다르지 않다.
이때 n[l]은 각 layer가 갖는 hidden size이다.
mini-batch의 크기에 따라 나머지 차원도 변할 것이다.
Implementing gradient descent
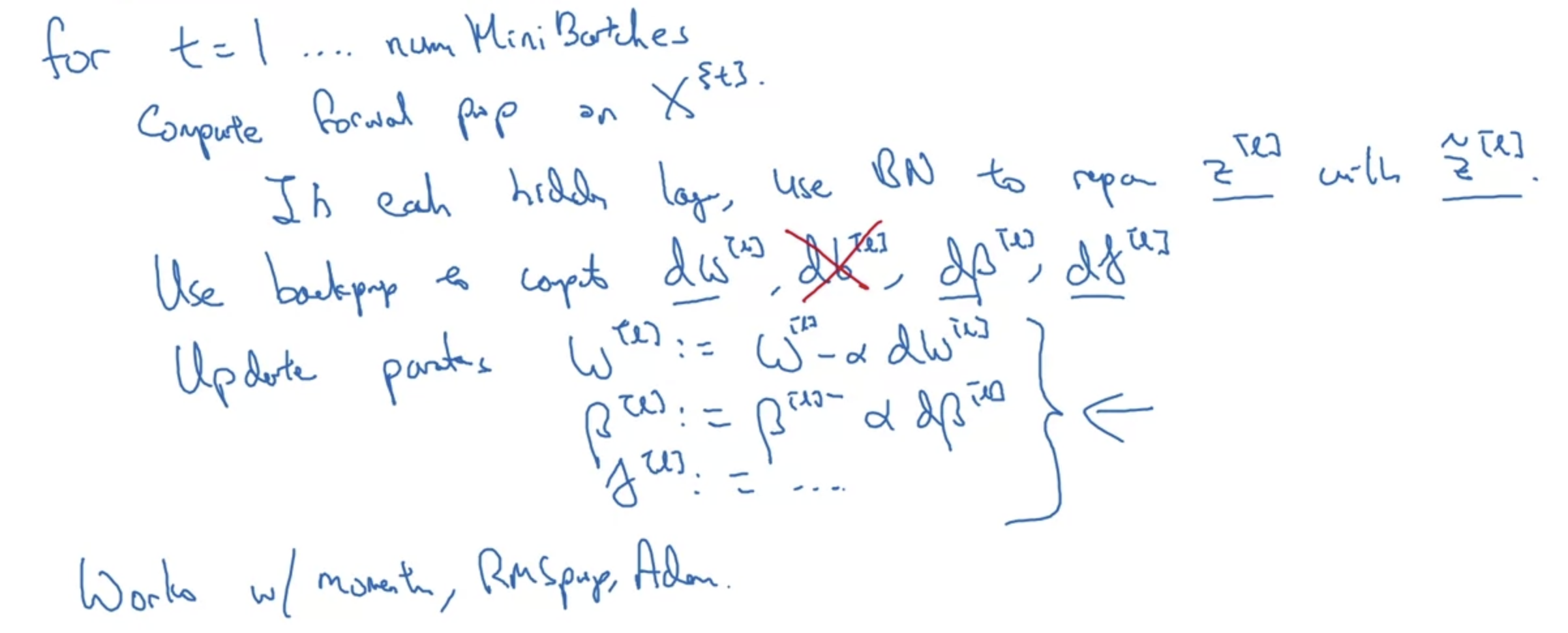
- 지금까지 공부한 Batch Normalization을 코드로 구현하면 위와 같은 모양이 될 것이다.
- 우선 forward하고 각 z에 대해 normalization을 적용한 뒤, backpropagation을 통해 W, gamma, beta를 update할 것이다.
- 여기서 backpropagation을 통해 세 변수를 업데이트하는 것은 이전에 공부한 optimizer인 Adam, RMSprop 등을 적용하는 것과 같은 역할을 한다.
따라서 위 방식 대신 다른 optimizer들을 사용하는 것도 방법이 될 수 있다는 것이다.
3. Why does Batch Norm work?
Learning on shifting input distribution

- 모델이 고양이인지 아닌지를 판별하는 학습을 하는 상황을 가정하자.
만약 왼쪽처럼 검은색 고양이에 대해서만 학습을 하게 된다면, 다양한 색의 고양이들에 대해서는 정확한 예측이 어려울 것이다. - 다시 말하자면 지금 학습하는 것이 잘 하고 있는 것처럼 보이더라도, 실제로는 굉장히 편향된 학습일 수 있다는 것이다.
- 이처럼 X와 Y를 mapping하는 문제에서 변수가 통째로 이동하는 것을 Covariate(공변량) Shift라고 하는데, 이 문제를 해결할 방법을 떠올려 보아야 한다.
Why this is a problem with neural networks?

- 이전에 비해 조금 더 복잡한 구조의 Neural Network가 존재한다고 가정해보자.
세 번째 혹은 네 번째 layer에 해당하는 변수들은 이전 layer들에 존재하는 변수들에 영향을 받을 것이다.
왜냐하면 각 layer에 입력으로 주어지는 변수 a는 이전 layer에서의 변수들로 계산되기 때문이다. - Normalization은 mean(평균)과 variance(분산)를 특정 값으로 고정시켜주기 때문에 이전 layer에서의 변수들로부터의 영향을 줄여준다.
다르게 말하자면 복잡한 구조를 가진 Network일수록 이전 layer에서의 Covariate Shift라는 문제점이 심각해질 수 있는데 이를 예방할 수 있다는 것이다.
Batch Norm as regularization

- Batch Norm은 우리가 의도했던 바와 달리 side effect(부작용)를 가질 수 있다.
Dropout 기법처럼 regularization의 효과를 가질 수 있다는 것이다. - 본래 Normalization은 변수들의 값을 조정하여 연산의 속도를 줄여주는 등의 효과를 가지는데, Batch Norm을 적용함으로써 noise가 추가되는 효과 또한 발생한다.
왜냐하면 기존의 연산에 mean을 빼고 variance로 나누는 등의 행위를 하기 때문이다. - 따라서 mini-batch를 기준으로 학습을 한다면 각 mini-batch에 대해 noise가 추가되는데, 이는 모델이 다양한 경우에 대해 보다 robust해지는 결과로 이어지게 된다.
이를 예상치 못한 side effect로 볼 수 있는 것은 이 효과가 의도하지 않더라도 발생할 수 있기 때문이다.
따라서 필요하다면 Batch Norm을 Dropout과 함께 사용하거나 하나만 사용하거나 할 수 있다. - 한편 mini-batch의 크기가 크면 클수록 noise는 줄어든다.
따라서 Batch Norm의 의도치 않은 side effect를 줄이고 싶다면 mini-batch size를 키우는 방식도 고려해 볼 수 있다.
4. Batch Norm at Test Time

- 왼쪽은 평균, 분산, 표준화, scaling의 식이다.
- mini-batch를 사용하는 경우 mini-batch 간 exponentially weighted average를 사용할 수 있다.
- train 동안에는 mini-batch 단위로 학습이 이뤄지지만 test 할 때는 각 항목을 따로 확인해야 한다.
예를 들어 mini-batch가 64인 경우, test에서는 mini-batch가 1인 셈이다.
이런 경우 train에서의 mini-batch가 가지는 평균을 estimate하여 test에 적용해야 한다. - 이때 사용되는 평균이 exponentially weighted average인 것이다.
- Exponentially Weighted Average 관련 포스팅 : https://chanmuzi.tistory.com/133
Optimization Algorithms(2) - Exponentially Weighted Averages
1. Exponentially Weighted Averages (지수 가중 평균) Temperature in London 영국의 1년 날씨를 날짜에 따라 표시한 그래프다. 전날과 오늘의 관계를 수식적으로 표현하여 그래프가 그려지는 양상을 예측하고자
chanmuzi.tistory.com
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 3주차' 카테고리의 다른 글
| Quiz & Assignment (0) | 2022.12.30 |
|---|---|
| Introduction to Programming Frameworks (0) | 2022.12.30 |
| Multi-class Classification (0) | 2022.12.24 |
| Hyperparameter Tuning (0) | 2022.12.18 |
