1. Softmax Regression
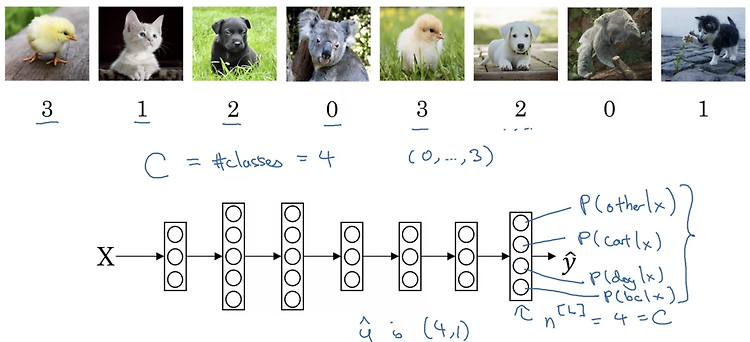
Recognizing cats, dogs, and baby chicks

- 이전에 다룬 내용은 두 개의 class로 분류하는 것이었습니다.
이를 테면 고양이인지 아닌지를 구분하는 binary classification이라고 할 수 있습니다. - 이번에는 두 개의 class가 아닌 여러 개의 class로 구분하는 상황을 가정해보겠습니다.
위 예시에서는 cat, dog, chick, others로 구분합니다. - 따라서 neural network의 output layer는 [4,1]의 shape을 갖게 되고 이 벡터는 입력 x가 주어졌을 때 각 class에 해당될 확률을 뜻하게 됩니다.
Softmax layer

- 여러 개의 class가 존재할 때 이를 분류하는 학습을 하는 network의 구조는 위와 같습니다.
- output layer에 Activation function인 softmax를 적용하기 위해서 변수 가중치 w와 편향 b로 구한 변수 z를 exponential 함수에 집어 넣습니다.
그리고 해당 layer에 존재하는 다른 z에 대해서도 같은 작업을 반복합니다. - 이렇게 구한 변수 t의 총합을 분모로, 각 t의 값을 분자로 삼아 분수를 만들게 되면 각 class에 해당할 확률을 구할 수 있게 됩니다.
구체적인 수치를 통한 예는 오른쪽에 나와 있습니다.
Softmax examples

- softmax를 linear하게 계산한 결과를 나타낸 crossfire(십자포화) 그래프 입니다.
단 하나의 layer에 대해 softmax를 적용하면 위와 같은 형태의 그래프가 나타납니다. - 색으로 표시된 면은 각 class를, 점들은 input을 통해 구해진 softmax의 output을 나타냅니다.
이 그림을 통해 정확히 분류된 것과 그렇지 않은 것들을 구분할 수 있습니다.
2. Training a Softmax Classifier
Understanding softmax

- softmax에 대한 내용을 다시 recap해보면 위와 같다.
단순히 가장 큰 값만 1로 취하고 나머지는 0으로 취하는 hard max와 다르기 때문에 soft max라는 이름을 붙인게 아닐까 싶다. - 이 강의에서 증명할 것은 아니지만 softmax를 통해 분류하고자 하는 class의 개수가 2개인 경우 logistic regression이 된다.
계산을 통해 얻어지는 최종 결과물이 2차원의 vector라는 점에 주목하면 된다.
Loss function

- classification을 위한 loss function으로 Cross Entropy를 사용한 예를 들어주셨다.
ground truth(정답)와 예측한 것의 확률을 곱하여 음수를 취해주면 loss가 된다.
이를 모든 케이스에 대하여 더한 것이 cost function이 된다. - class가 네 개라고 가정한 경우, 연산이 끝난 최종 결과물은 (4, m) size의 matrix가 된다.
여기서 4는 class의 개수를, m은 example의 개수를 뜻한다.
Gradient descent with softmax

- forward에서 softmax를 통해 구한 결과 y hat에 대해 backpropagation을 수행하는 것은 이전에 배운 것들과 동일하다.
당연히도 이를 직접 계산할 필요도 없으며 framework를 사용할 때는 단순히 forward에만 집중하더라도 backward는 자동적으로 해결할 수 있다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 3주차' 카테고리의 다른 글
| Quiz & Assignment (0) | 2022.12.30 |
|---|---|
| Introduction to Programming Frameworks (0) | 2022.12.30 |
| Batch Normalization (0) | 2022.12.22 |
| Hyperparameter Tuning (0) | 2022.12.18 |