Improvement 1: weighting
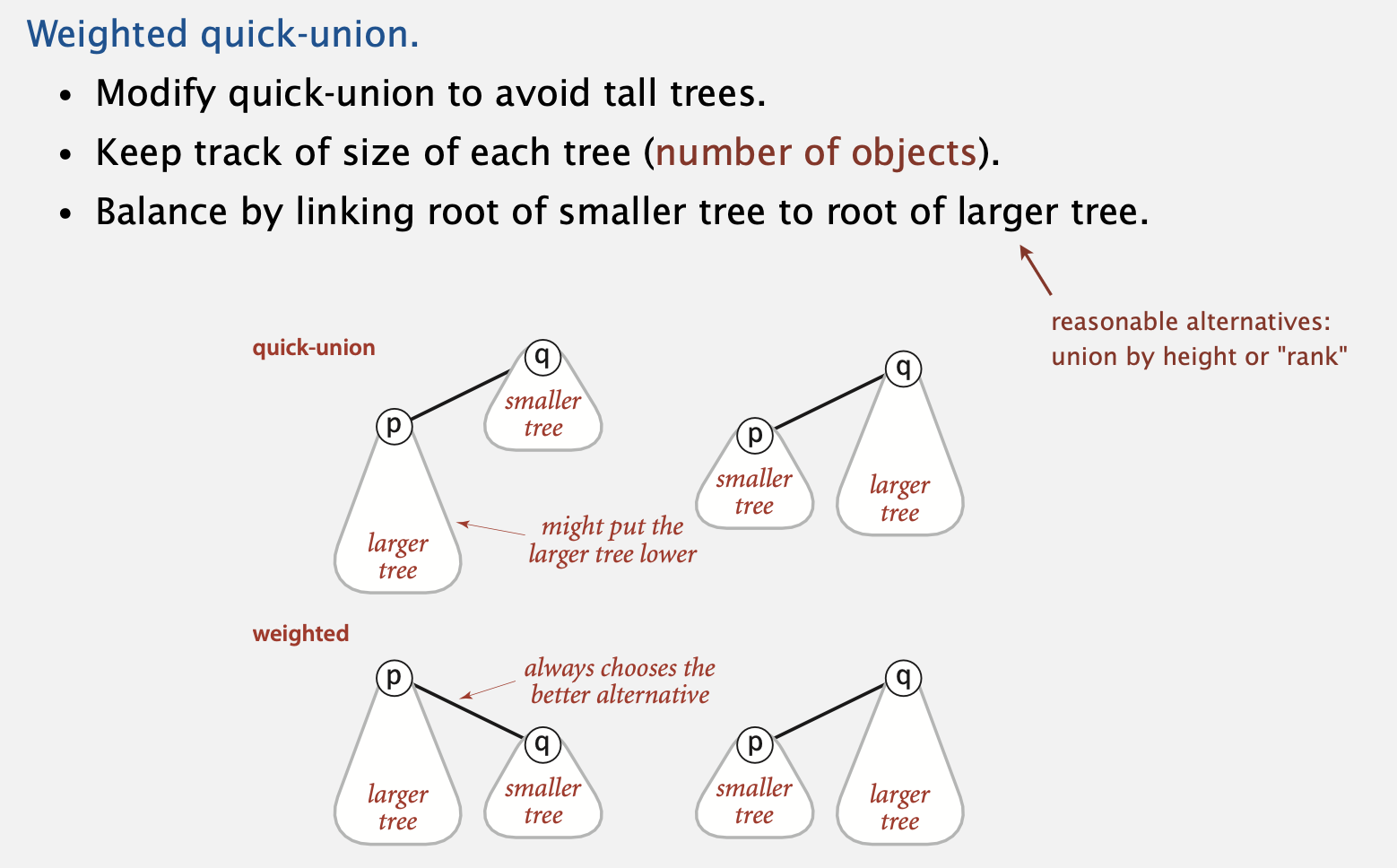
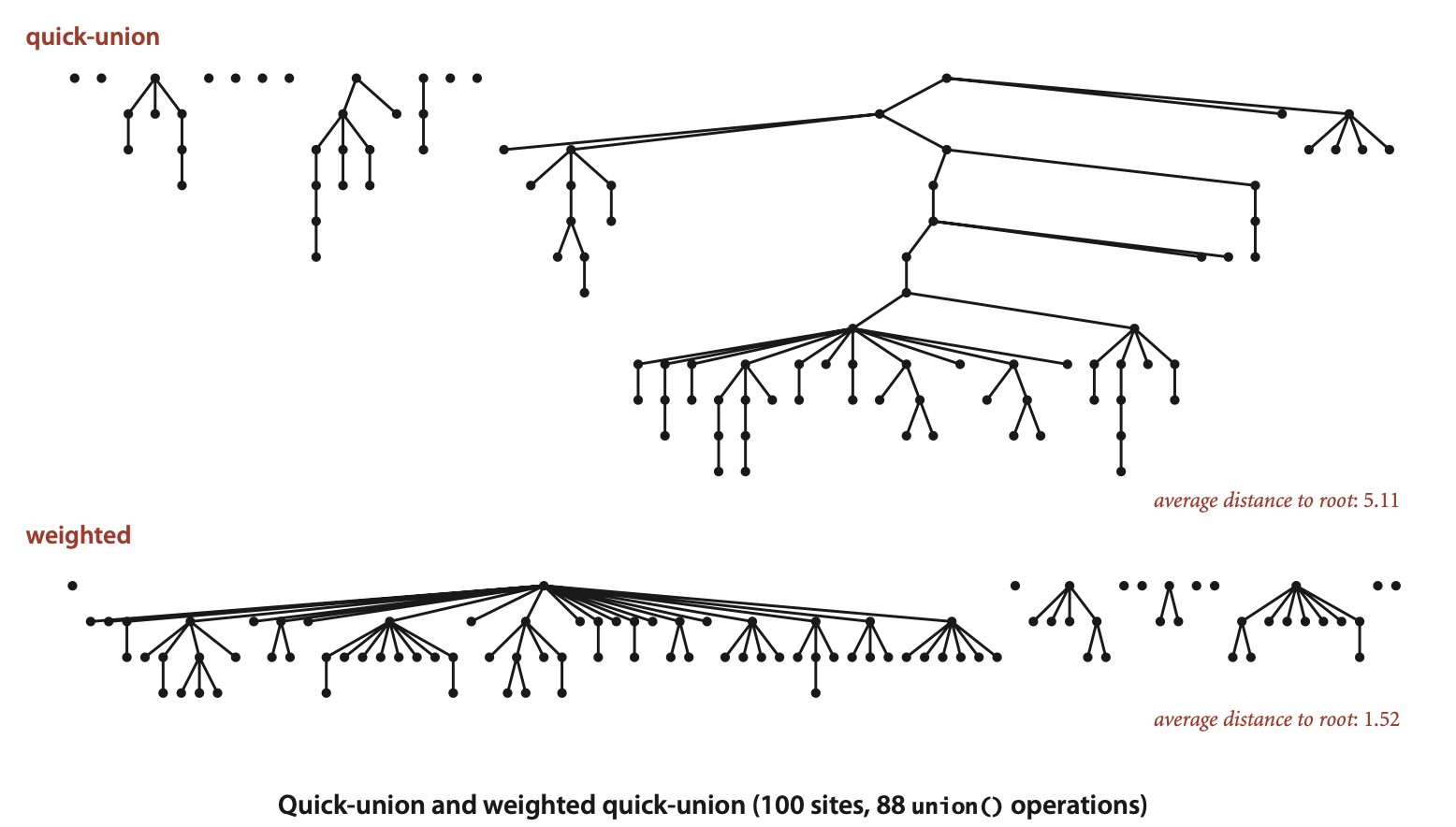
- 기존의 quick-union의 속도 문제를 개선하기 위한 weighted quick-union입니다.
- 더 큰 트리가 위에 위치합니다. 즉, 작은 트리가 아래에 위치합니다 → worst case를 방지할 수 있습니다.
- 작은 트리의 루트를 큰 트리의 루트와 연결합니다.
- 우측의 그림은 기존의 union과 weighted 방식으로 개선된 union의 결과를 도식화 한 것입니다.
Weighted quick-union: Python implementation
class Weighted_Quick_Union_UF(n):
id = [x for x in range(n)]
sz = [1 for _ in range(n)] # tree 내 원소 개수
def root(i):
while i != id[i]: # 자기 자신이 root가 될 때까지
i = id[i]
return i
def connected(p, q): # root 같으면 True
return root(p) == root(q)
def union(p, q): # 자식, 부모
i, j = root(p), root(q)
if i == j:
return
if sz[i] < sz[j]: # q 트리가 더 크면
id[i] = j # q 트리가 부모
sz[j] += sz[i] # q 트리 원소 증가
else: # p 트리가 더 크면
id[j] = i
sz[i] += sz[j]
Weighted quick-union analysis
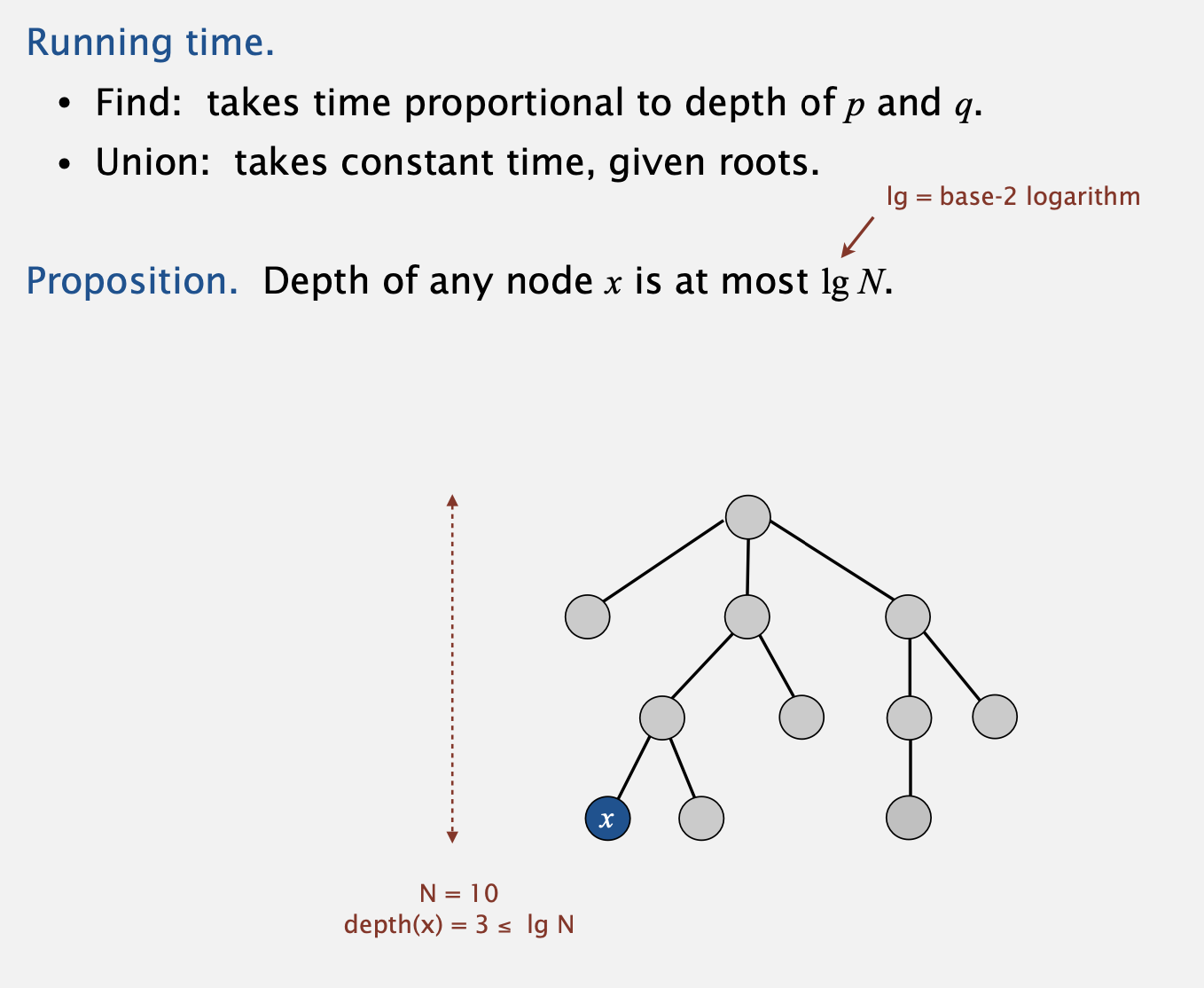
- Find 명령은 p와 q의 깊이에 비례하여 시간이 걸릴 것입니다.
한편 Union 명령은 루트에 따른 상수 시간이 걸립니다. - 이전의 Quick Union과 비교했을 경우, 트리의 깊이가 아무리 깊어도 최대 logN입니다.
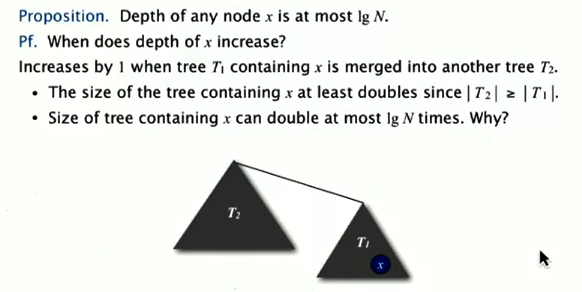
(이때 log는 밑을 2로 갖는 log입니다)- 왜일까요? 만약 x라는 노드의 깊이가 한 층 더 깊어지려면, x가 속한 tree의 크기가 최소 2배 이상은 되어야 하기 때문입니다.
예를 들어 x가 속한 T1의 크기가 3이라고 가정하죠.
이때 이 트리가 속하게 될 T2의 크기는 적어도 6이상이어야 합니다. 그래야지만 T1이 T2에 속하면서 밑으로 들어가 X의 깊이가 증가하기 때문이죠.
(아래 표를 참고해주세요)
- 왜일까요? 만약 x라는 노드의 깊이가 한 층 더 깊어지려면, x가 속한 tree의 크기가 최소 2배 이상은 되어야 하기 때문입니다.
- 따라서 훨씬 효율적인 알고리즘이라는 것을 알 수 있습니다.
| x의 깊이 | 0 | 1 | 2 | 3 | 4 | ... | log N |
| tree의 크기 | 1 | 2 | 4 | 8 | 16 | ... | N |

- 표에서 볼 수 있듯이 union, connected의 시간 복잡도가 log 단위로 내려가서 획기적으로 시간을 아낄 수 있습니다.
Improvement 2: path compression
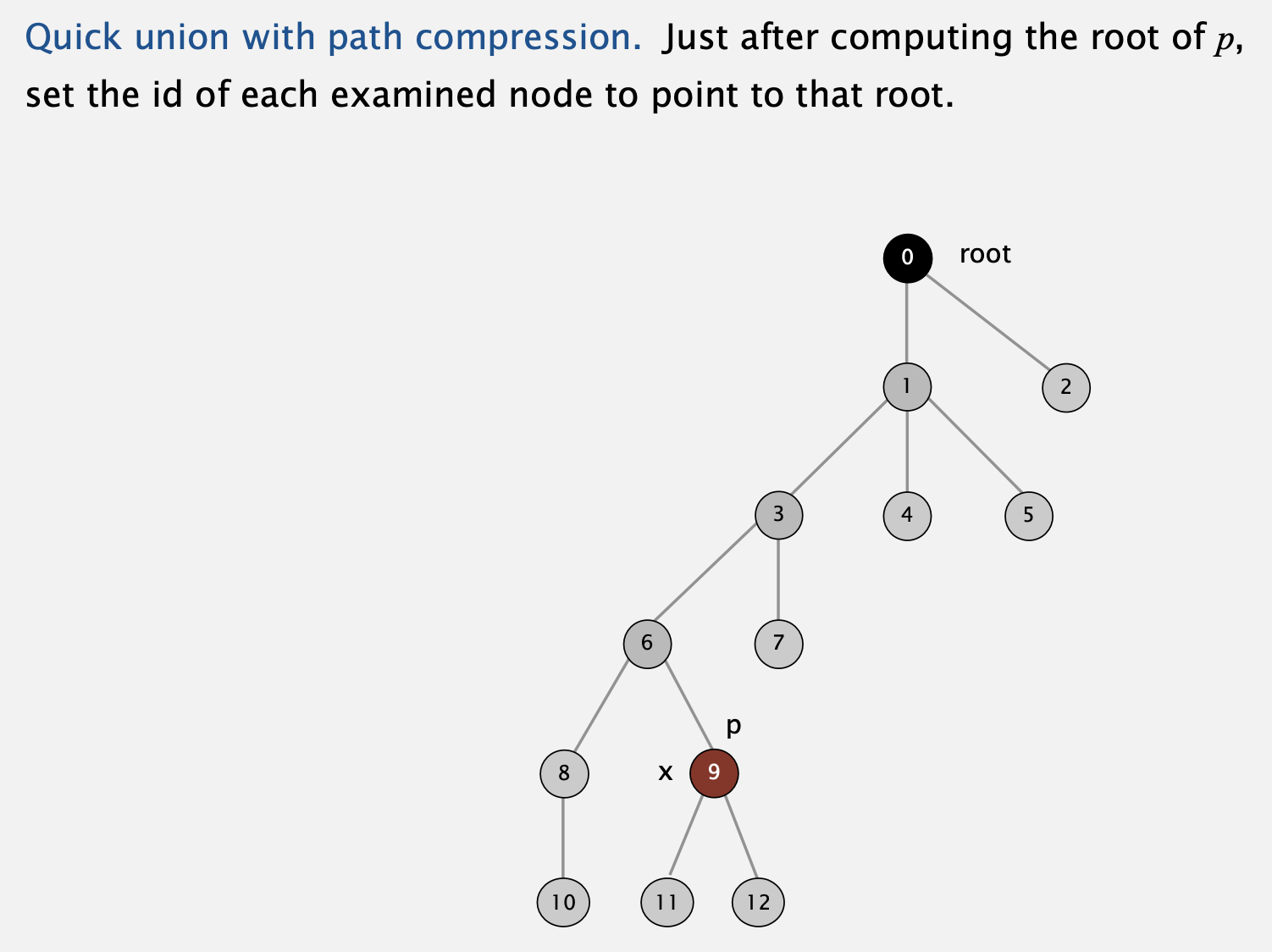
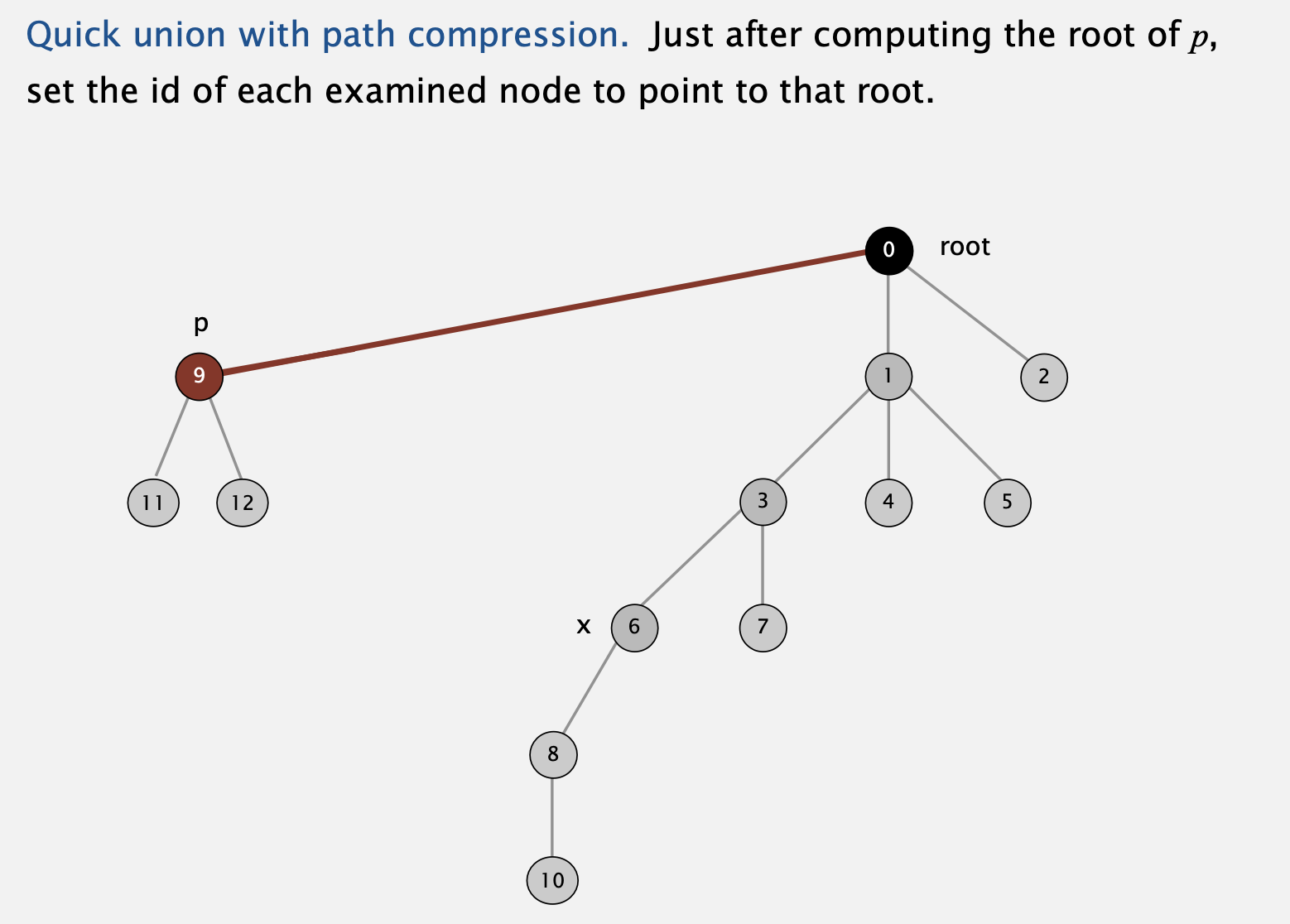
- 노드 9를 예시로 든다면, 굳이 이것의 root를 6으로 둘 필요가 없습니다.
이것의 최종 root인 0을 가리키도록 변경하면 깊이가 줄어들어 find 과정이 훨씬 효율적일 것입니다. - 물론 이 과정이 굉장히 간단하게 진행되어야지만 기존보다 효율적이겠죠.
Path compression: Python implementation

class Weighted_Quick_Union_UF(n):
id = [x for x in range(n)]
sz = [1 for _ in range(n)] # tree 내 원소 개수
def root(i):
while i != id[i]: # 자기 자신이 root가 될 때까지
id[i] = id[id[i]] # 한 줄 추가!
i = id[i]
return i
def connected(p, q): # root 같으면 True
return root(p) == root(q)
def union(p, q): # 자식, 부모
i, j = root(p), root(q)
if i == j:
return
if sz[i] < sz[j]: # q 트리가 더 크면
id[i] = j # q 트리가 부모
sz[j] += sz[i] # q 트리 원소 증가
else: # p 트리가 더 크면
id[j] = i
sz[i] += sz[j]- 이번에도 파이썬으로 코드를 작성한 결과입니다.
딱 한 줄이 추가되었고, 이를 통해 트리를 굉장히 평평(flat)하게 만들 수 있습니다.
Weighted quick-union with path compression: amortized analysis

- log * N은 N을 1로 바꾸기 위해 log N을 취해야 하는 횟수를 나타내는 함수입니다.
이를 iterate log function(반복 로그 함수)라고 부릅니다. - 따라서 이 알고리즘은 log * N만큼의 시간, 즉 (거의) 선형시간으로 바꾼 획기적인 알고리즘으로 평가하고 있습니다.
Summary

출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(1) : Analysis of Algorithms Introduction (0) | 2023.04.02 |
|---|---|
| Union-Find(5) : Union-Find Applications (0) | 2023.04.01 |
| Union-Find(3) : Quick Union (0) | 2023.03.31 |
| Union-Find(2) : Quick Find (0) | 2023.03.31 |
| Union-Find(1) : Dynamic Connectivity (0) | 2023.03.31 |
