이번 강의는 왜 알고리즘에 대한 분석을 해야 하는지, 그리고 효율적인 알고리즘을 짜는 것이 왜 중요한지에 대해 다룹니다.
사실 지금까지 알고리즘에 대한 인식은 그저 문제 풀이용, 두뇌 회전용이라고 생각했었는데 확실히 대학 수업이라 그런지 다르네요.
Cast of characters

- 현실 세계에는 여러 역할과 각 역할에 맞는 요구사항들이 있습니다.
공부하는 학생은 그런 여러 입장을 모두 경험할 때가 있구요.
Running time

- 실행 시간, 내가 어떤 작업을 수행하는데 걸린 시간이 얼마나 되는지를 파악하는 것은 오래전부터 있던 일인가봅니다.
그림에 나온 것처럼, 예전의 기계들이라면 '축이 몇 번 돌아가는지'가 기준이 되기도 했겠죠.
Reasons to analyze algorithms

- 알고리즘을 분석하는 여러 이유가 있겠지만 당연히 효율성을 위해서입니다.
지금이야 연산이 무척 빠르고 좋은 컴퓨터들이 많지만, 그만큼 데이터도 많고 작업도 무거워졌죠.
어떤 일이든지간에 효율적으로 일을 처리할 수 있게끔 만드는 것은 프로그래머의 중요한 역량일 것입니다.
Some algorithmic successes
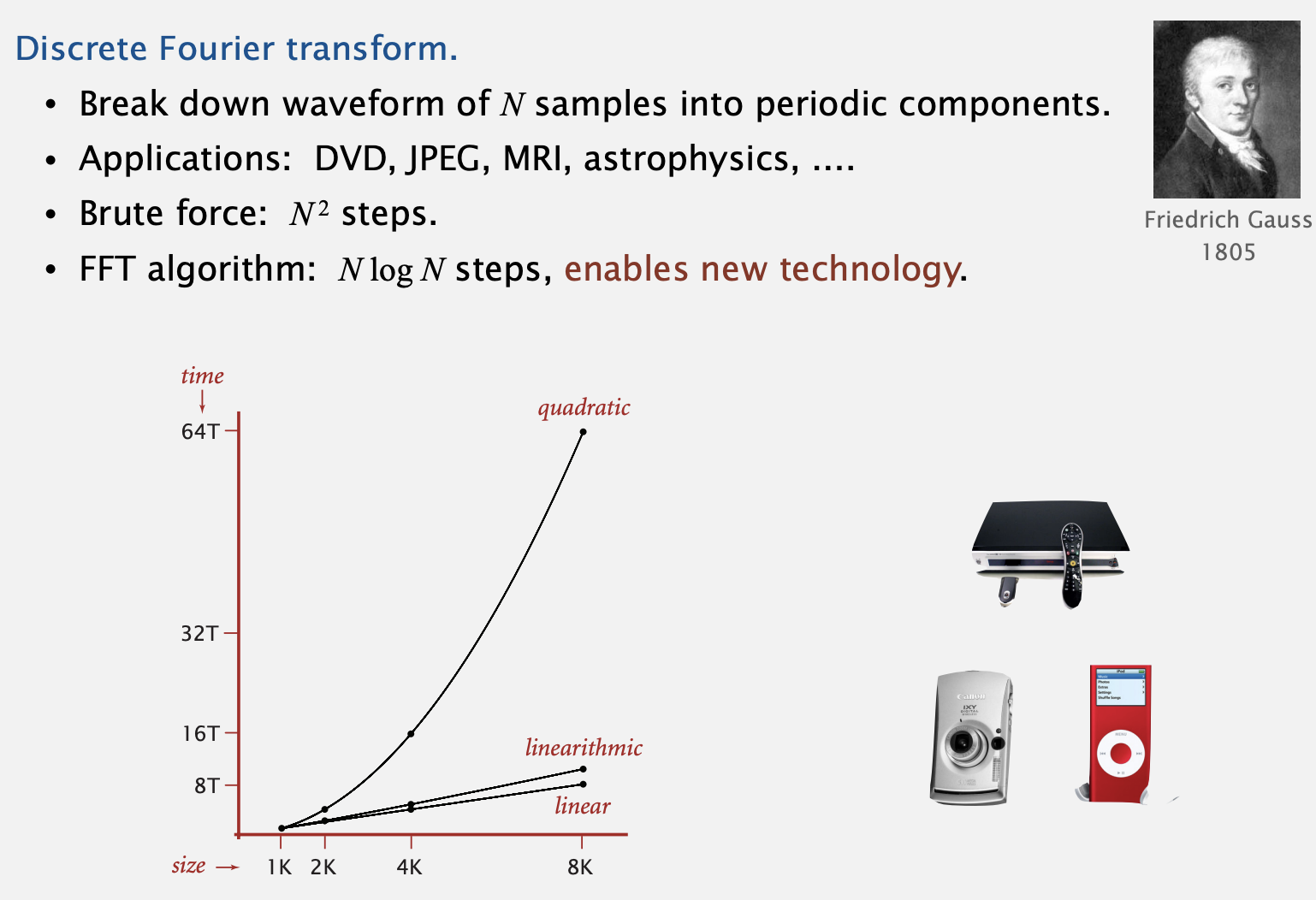
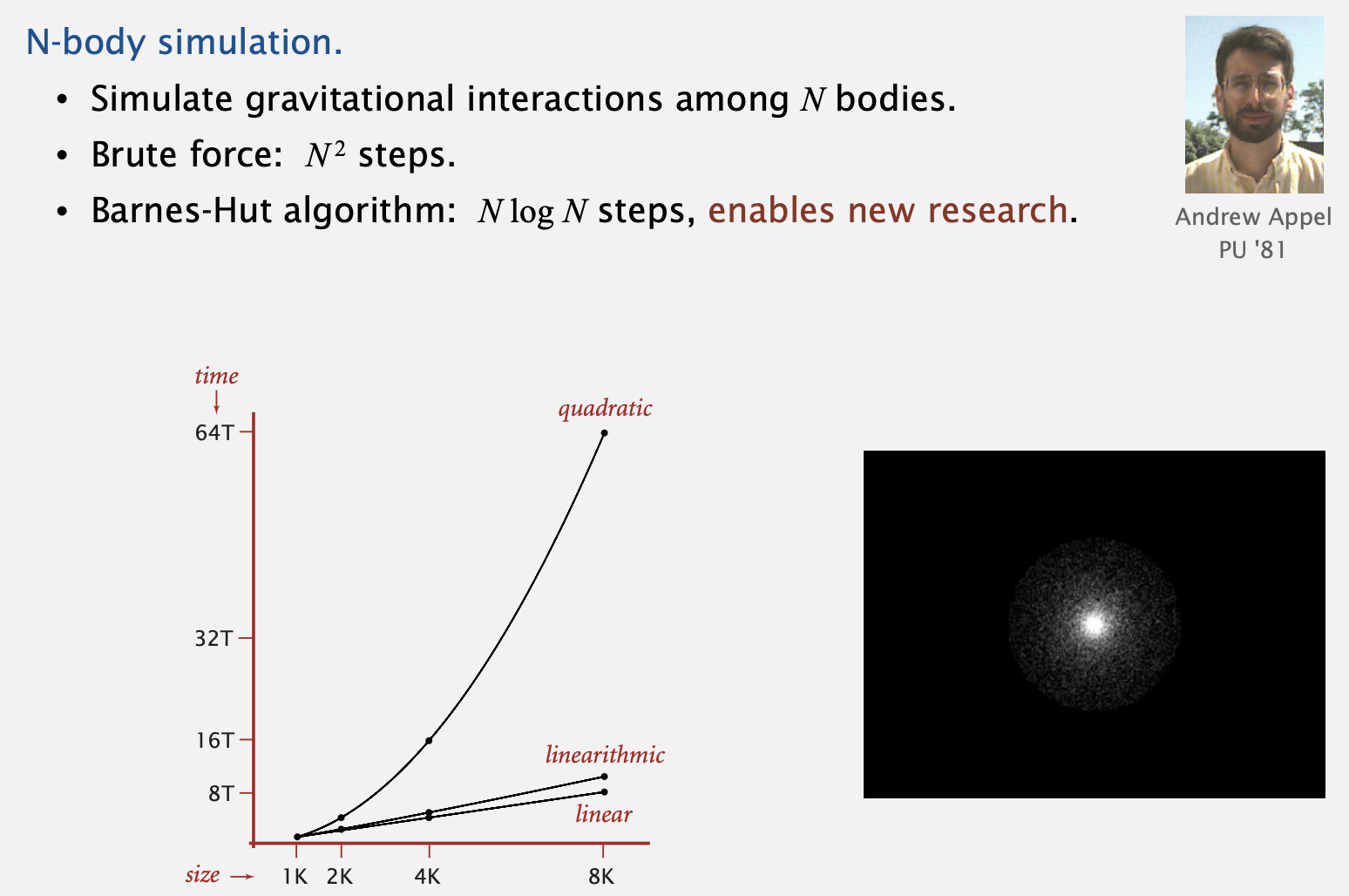
- 알고리즘을 개선하여 획기적인 변화를 불러온 두 사례입니다.
사실 우리는(저는 ㅎㅎ..) 이런걸 봐도 큰 감흥이 없습니다.
당연히 좋아졌으니까, 더 효율적이니까 혁신이었겠지~하고 마는데요.. - 그래서 실제 계산이 얼마나 차이나는지 생각해보면 좀 잘 와닿습니다.
예를 들어 n이 1,000,000(백만)인 상황을 생각해봅시다.
기존의 O(N^2) 복잡도인 경우 1,000,000,000,000(1조)번의 연산이 필요합니다. - O(N logN)은 어떨까요? log (1,000,000)은 약 20입니다.
(밑이 2인 로그입니다! 이는 모든 log를 그렇게 계산한다는 것이 아니라 보통 복잡도가 log인 경우 밑이 2가 되는 경우가 많습니다)
그러면 총 20,000,000번의 연산으로 작업이 끝납니다. - 둘을 비교하는 것은 사실 N^2 / N logN = N / logN = 1,000,000 / 20 = 50,000이 됩니다.
즉, 후자가 기존에 비해 50,000배나 빠르다는 뜻이죠. - 어떤 명령을 수행하는데 예를 들어 50,000일이 걸린다고 생각해봅시다.
50000 / 365 = 약 137입니다.
즉 137년이 걸리는 일이기 때문에 살아 생전에 결과물을 보지 못하게 되겠죠.
이건 10년뒤에 100배나 연산을 빠르게 하는 컴퓨터를 가져와도 500일이 더 걸리는 상황일 것입니다.
근데 만약 알고리즘을 개선하면 단 하루만에 작업이 끝나는 것이죠. - 컴퓨터가 지금보다 5만배나 빠른 연산을 할 수 있게 되는 것을 기다리는 것보다 훨씬 효율적이죠?
The challenge & Scientific method applied to analysis of algorithms


- 결국 어떤 알고리즘 혹은 프로그램이 효율적이냐 그렇지 않냐 등을 어떻게 분석할지에 대한 고민이 필요합니다.
- 과학적인 접근 방법을 공식화해놓기도 했지만 가장 중요한 원칙은 두 가지입니다.
1) 재생산 가능해야 한다. 즉, 동일한 조건에서 명령을 수행했을 때 동일한 결과가 나와야한다(재현 가능하다)는 것입니다.
2) 가설은 반증가능해야합니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(3) : Mathematical Models (0) | 2023.04.02 |
|---|---|
| Analysis of Algorithms(2) : Observations (0) | 2023.04.02 |
| Union-Find(5) : Union-Find Applications (0) | 2023.04.01 |
| Union-Find(4) : Quick-Union Improvements (0) | 2023.04.01 |
| Union-Find(3) : Quick Union (0) | 2023.03.31 |
