Union-find applications

- 네.. 뭐.. 이렇게 다양한 분야에 Union-Find 알고리즘이 사용될 수 있다고 하네요!
Percolation
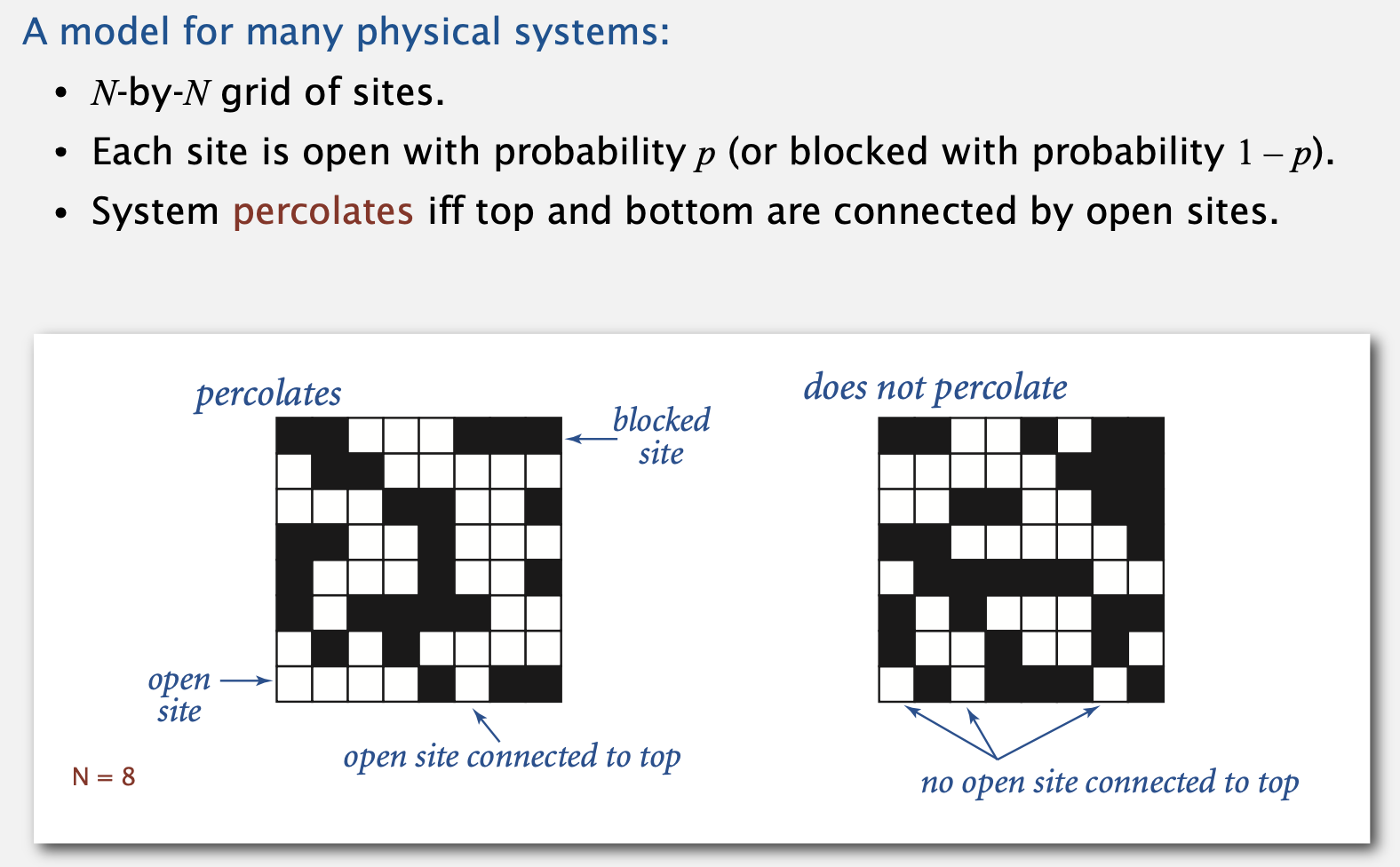
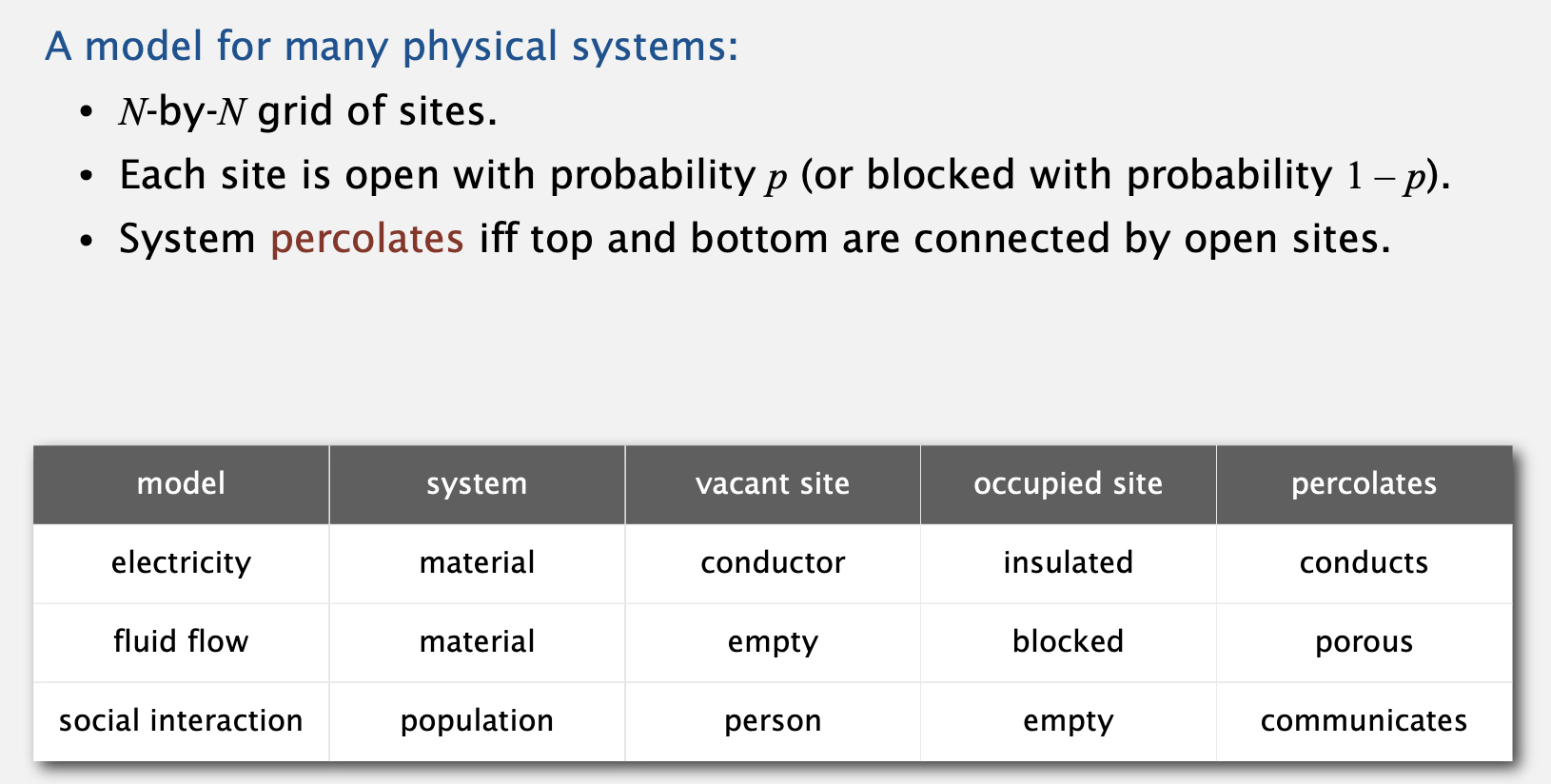
- 과제로 제시되는 문제는 percolation(여과, 투과)입니다.
- N * N 사이즈의 격자판이 존재합니다.
- p의 확률로 격자가 오픈되어 있고, 1-p의 확률로 격자가 닫혀있습니다.
- 격자의 맨 위부터 아래까지 연결되면 percolate라고 판정합니다.
- 이 알고리즘은 전기, 유동 액체, 사회적 상호작용 등에 적용 가능한 알고리즘이라고 합니다.
Likelihood of percolation

- 공간이 open / closed(1-open) 될 확률에 따라 시스템이 percolate 할지 안할지 달라지겠죠.
p의 값을 조정하면서 그 결과가 어떻게 되는지를 시각화한 것입니다.
Percolation phase transition
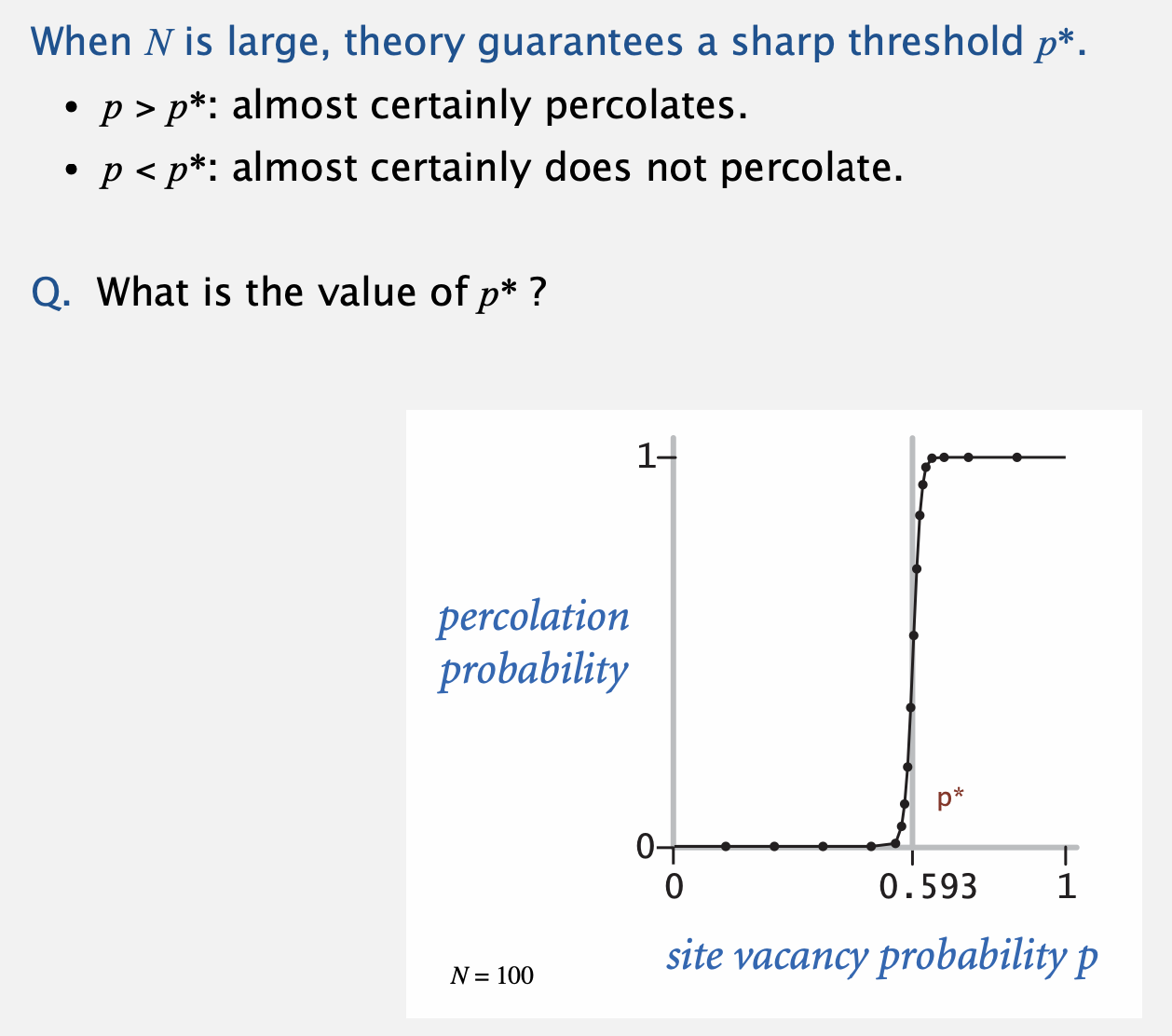
- 따라서 각 격자가 open / closed 될 확률을 나타내는 p의 값에 따라 이 시스템이 percolate할 확률이 결정됩니다.
- 이것은 일정한 threshold를 가지는데요, 왜 0.593이되면 갑자기 percolation 확률이 치솟는지에 대해서는 증명되지 않았다고 합니다.
다만 저 값이 threshold가 된다라는 것은 프로그래밍을 통해 입증된 것이라고 하네요.
Monte Carlo simulation

- Monte Carlo 시뮬레이션을 통해 위에서 언급한 p의 변화에 따른 percolation 확률을 확인할 수 있습니다.
- 닫힌 격자 중 하나를 열고, 인접한 (최대) 4개 지역과 union 합니다.
- 이때 주변이 여전히 닫혀있거나,
- 격자판 바깥이거나,
- 이미 열려 있는 경우,
- 는 당연히 union되지 않습니다. 따라서 상황에 따라 union 개수가 달라질 수 있다는 뜻입니다.
Dynamic connectivity solution to estimate percolation threshold
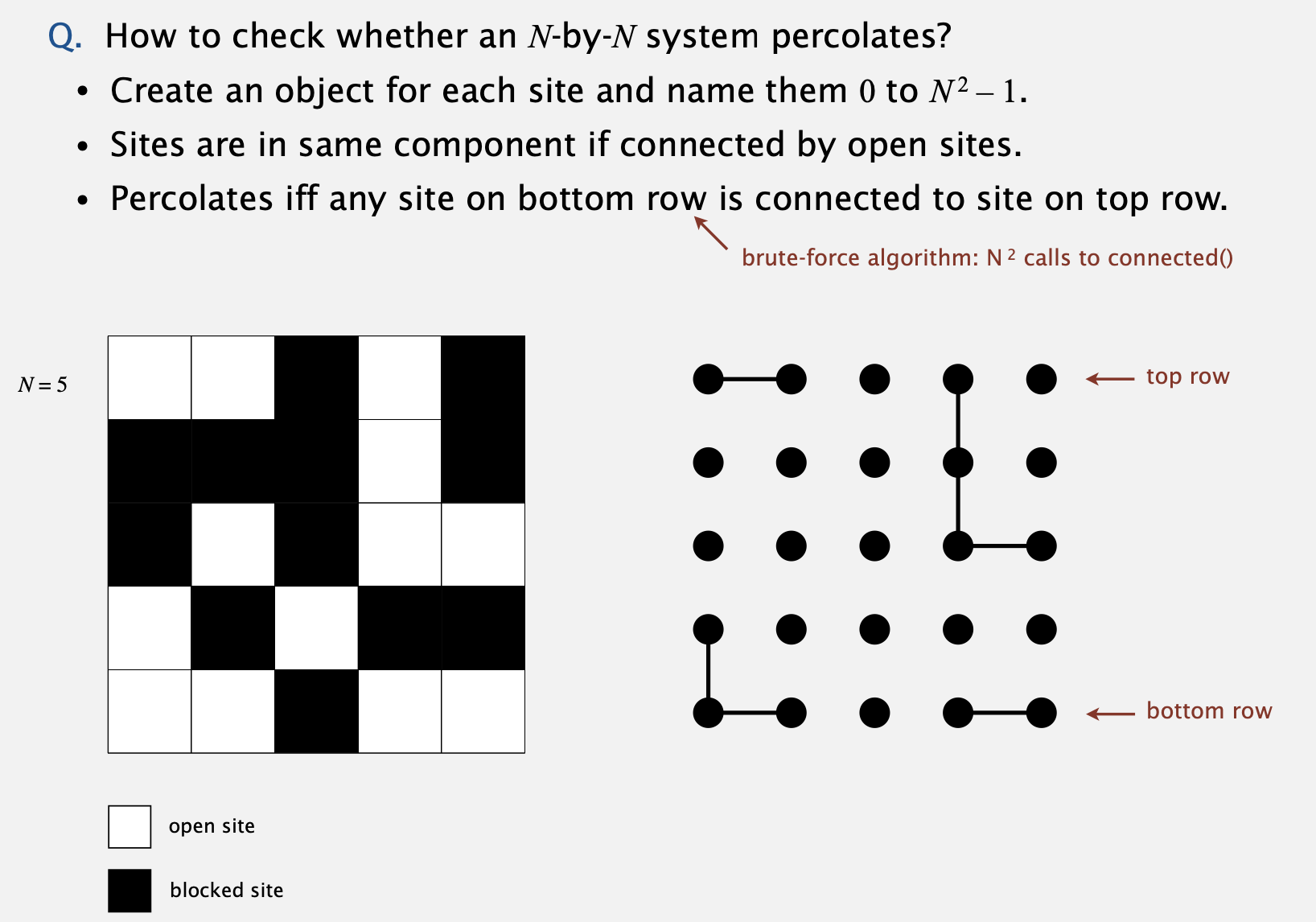
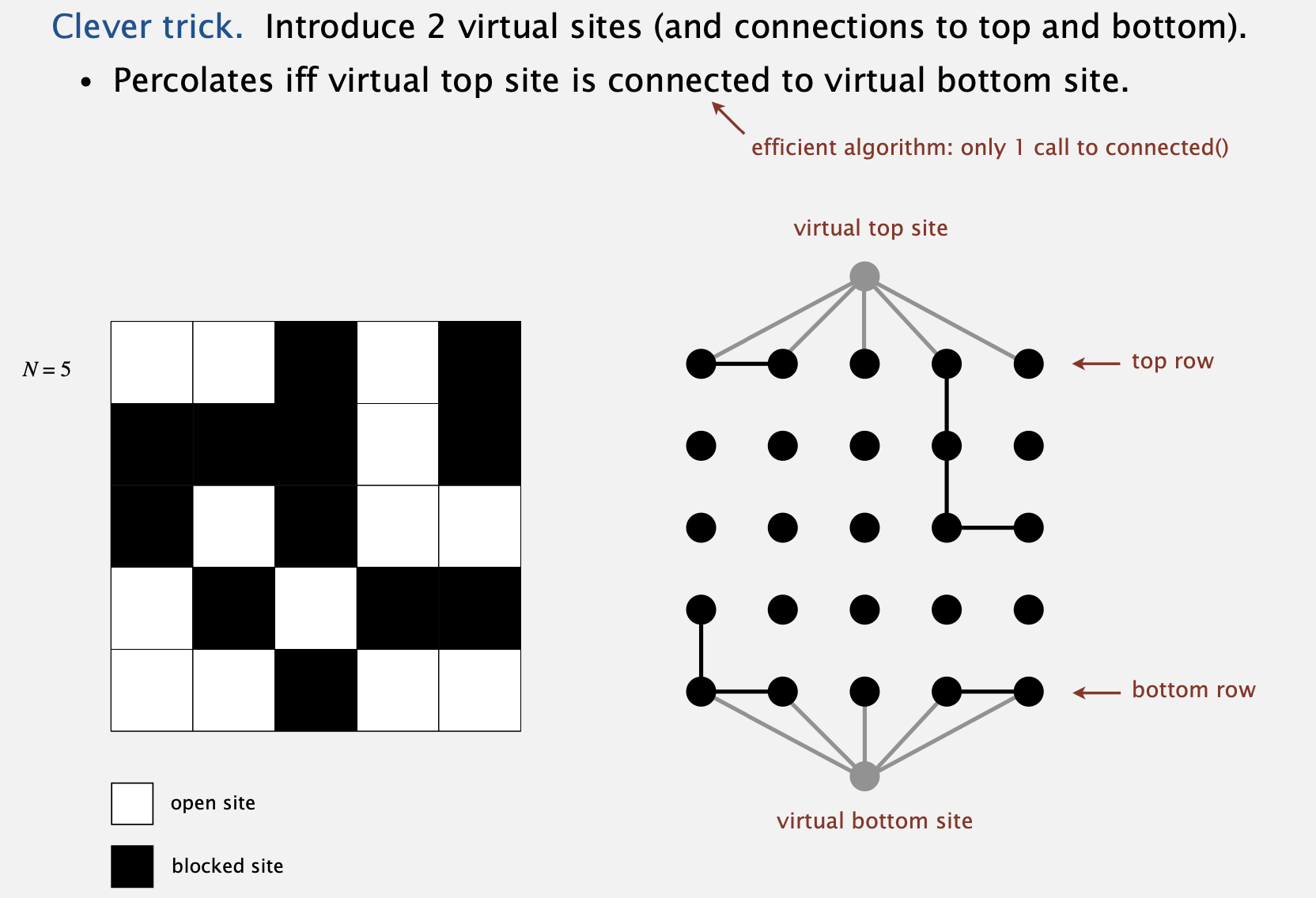
- 그럼 이 시스템이 percolate하는지 안하는지 확인은 어떻게 할까요?
- N * N 사이즈의 격자판을 따로 만들어 연결 상태를 확인할 수 있습니다.
- 맨 바닥 중 어떤 격자 하나라도 맨 위와 연결이 되어 있다면 percolate 판정을 줄 수 있겠죠.
- 이를 위해 가상의 top / bottom 사이트를 만드어서 계산하는 것이 훨씬 간편하다고 합니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(2) : Observations (0) | 2023.04.02 |
|---|---|
| Analysis of Algorithms(1) : Analysis of Algorithms Introduction (0) | 2023.04.02 |
| Union-Find(4) : Quick-Union Improvements (0) | 2023.04.01 |
| Union-Find(3) : Quick Union (0) | 2023.03.31 |
| Union-Find(2) : Quick Find (0) | 2023.03.31 |
