Common order-of-growth classifications


- 알고리즘을 효율성에 따라 구분하면 위와 같습니다.
- 모델의 사이즈가 커져도 처리하는 시간이 크게 증가하지 않는 constant(상수), logarithmic(로그)
- 모델의 크기와 거의 비례하는 linear(선형), linearithmic
- 모델이 커지는 것보다 더 많은 시간을 필요로 하는 quadratic(이차), cubic, exponential(지수)
Practical implications of order-of-growth

Binary search demo

- 아주 효율적인 탐색 알고리즘인 이진 탐색(binary search) 알고리즘입니다.
- 이 알고리즘은 배열 내 값들이 오름차순으로 정렬되어 있다는 것을 전제로 삼습니다.
- 반복적으로 배열의 중간값을 찾고 이를 찾고자 하는 값과의 대소비교를 통해 좌우로 탐색을 반복 수행합니다.
- 결과적으로 탐색의 범위는 계속해서 2배씩 줄어들기 때문에 logN 의 시간복잡도를 가집니다.
Binary search: Python implementation
- 저는 자바를 잘 쓸 줄 모르기 때문에 ㅎㅎ.. 파이썬으로 코드를 바꿔서 작성해보겠습니다.
def binary_search(arr, key):
low, high = 0, len(arr)-1
while low <= high:
mid = low + (high-low) // 2 # 중간 위치 찾기
if key < arr[mid]: # key가 왼쪽에 있음
high = mid -1
elif key > arr[mid]: # key가 오른쪽에 있음
low = mid + 1
else: # key가 mid랑 동일함
return mid
return -1 # low > high가 될 때까지 key값이 존재하지 않음- 코드의 의미는 주석으로 표시해두었습니다.
배열의 중간값과 내가 찾고자 하는 key의 값을 계속 비교하면서,
만약 key값이 중간보다 작다면 왼쪽으로 추가 탐색을, 반대라면 오른쪽으로 추가 탐색을 반복하는 알고리즘입니다.
Binary search: mathematical analysis

- 얼마만큼의 복잡도를 가지는지에 대한 증명도 재귀적으로 이뤄졌습니다.
- 탐색 범위를 반으로 줄여나가면서 증가하는 탐색 횟수를 더하다보면 최종적으로 1 + logN의 시간복잡도라는 것을 알 수 있습니다.
- 심지어 이는 N이 꼭 짝수가 아니더라도 동일하게 적용가능합니다(그래서 제 코드에도 // 연산자를 사용했습니다)
An N^2 log N algorithm for 3-Sum

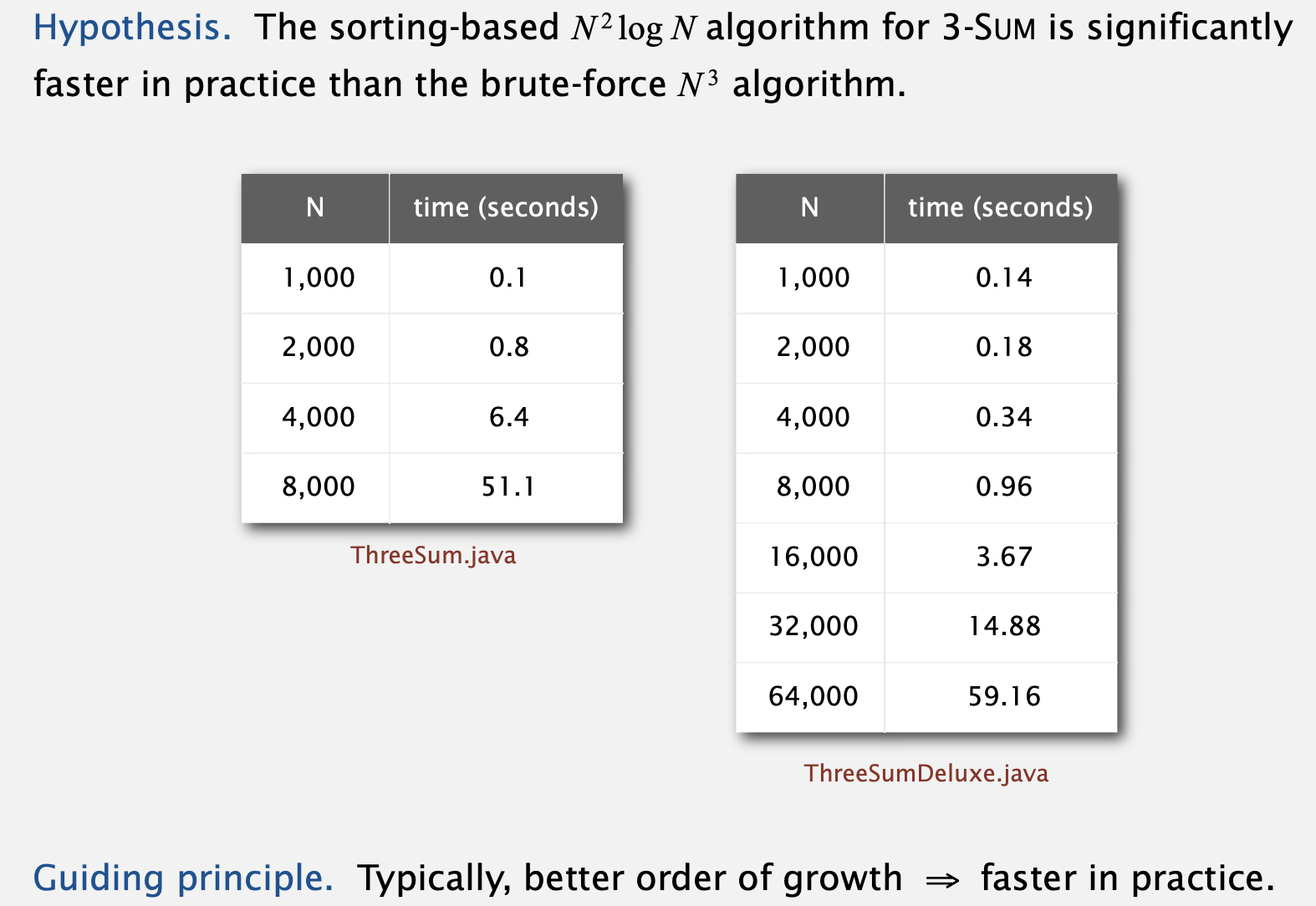
- 그래서 정렬된 배열에 대한 이진 탐색 알고리즘을 적용한 3-Sum은 엄청나게 좋은 효율을 보여줍니다.
- 우측 사진에서 N=8,000일 때부터의 값을 비교해보면 그 차이가 정말 명확하죠.
- 로직도 엄청나게 간단합니다.
- 1 ) N개의 숫자를 오름차순 정렬한다.
- 2) (i, j) 쌍에 대해 배열의 나머지 값 중에 -(i + j) 값이 존재하는지 찾는다.
- 삽입 정렬 알고리즘을 사용하면 오름차순 정렬은 N^2의 시간 복잡도를 가집니다.
- (i, j) 쌍은 N^2번 수행되며 매 탐색은 logN의 시간복잡도를 가지므로 총 N^2*logN의 시간복잡도가 됩니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(6) : Memory (0) | 2023.04.03 |
|---|---|
| Analysis of Algorithms(5) : Theory of Algorithms (0) | 2023.04.03 |
| Analysis of Algorithms(3) : Mathematical Models (0) | 2023.04.02 |
| Analysis of Algorithms(2) : Observations (0) | 2023.04.02 |
| Analysis of Algorithms(1) : Analysis of Algorithms Introduction (0) | 2023.04.02 |
