Example: 3-Sum & brue-force algorithm


- 배열 내의 세 원소 합이 0이 되는 경우의 수를 구하는 알고리즘입니다.
- 생각이 필요 없는 아주 단순한 풀이 방식을 생각하면 brute force 방식을 떠올릴 수 있을 것입니다.
- 이때 i, j, k가 원소의 개수 n만큼 탐색하는 방식입니다.
- 따라서 시간 복잡도는 무려 O(N^3)으로 엄청나게 비효율적입니다.
Measuring the running time


- 나의 알고리즘이 작동하는데 얼마만큼의 시간이 소요되는지 측정하는 방법은 다양하겠지만...
직접 스톱워치를 재는 경우는 없겠죠? - 대부분은 저런 코드를 사용해서 실행 시간을 측정하곤 합니다.
파이썬에도 time 모듈이 있어서 알고리즘의 효율성을 판단할 수 있습니다.
Empirical & Data analysis

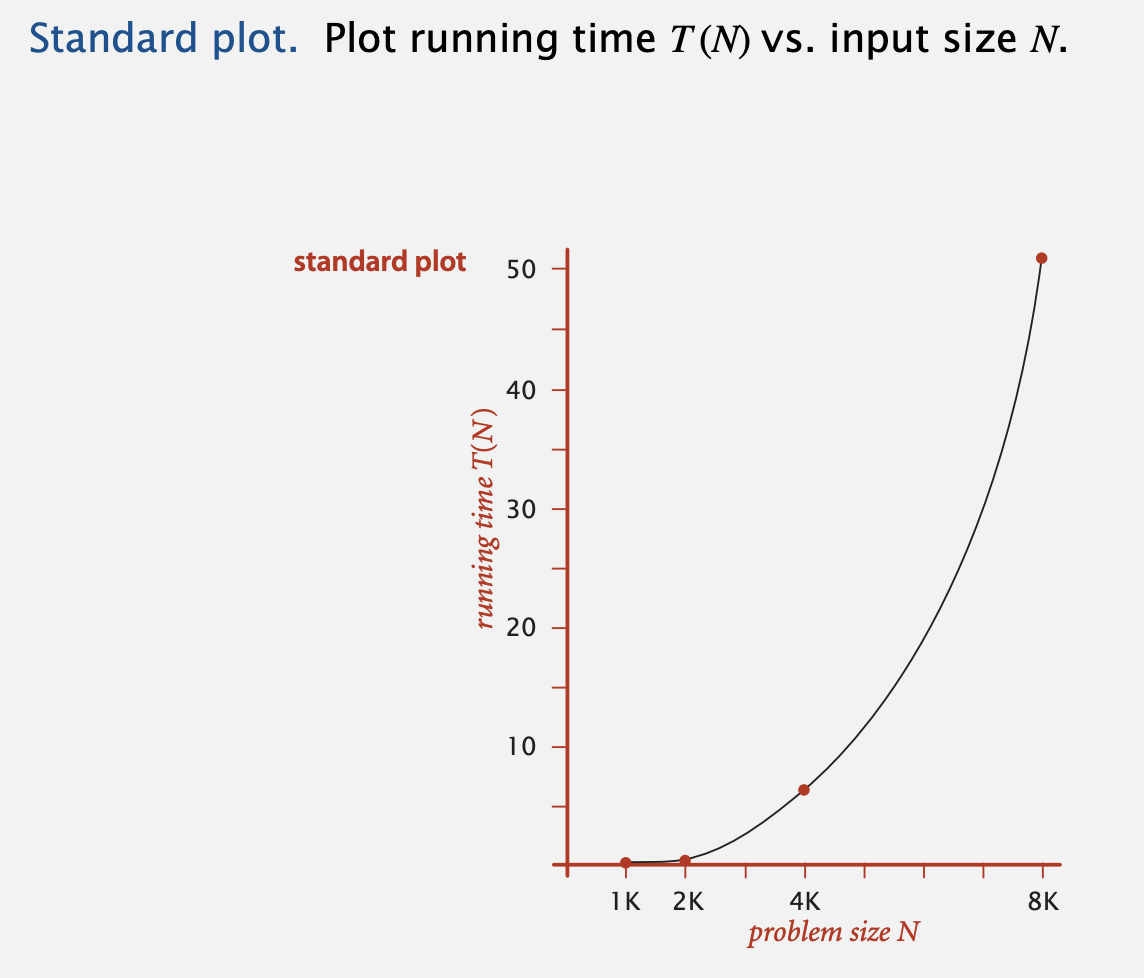
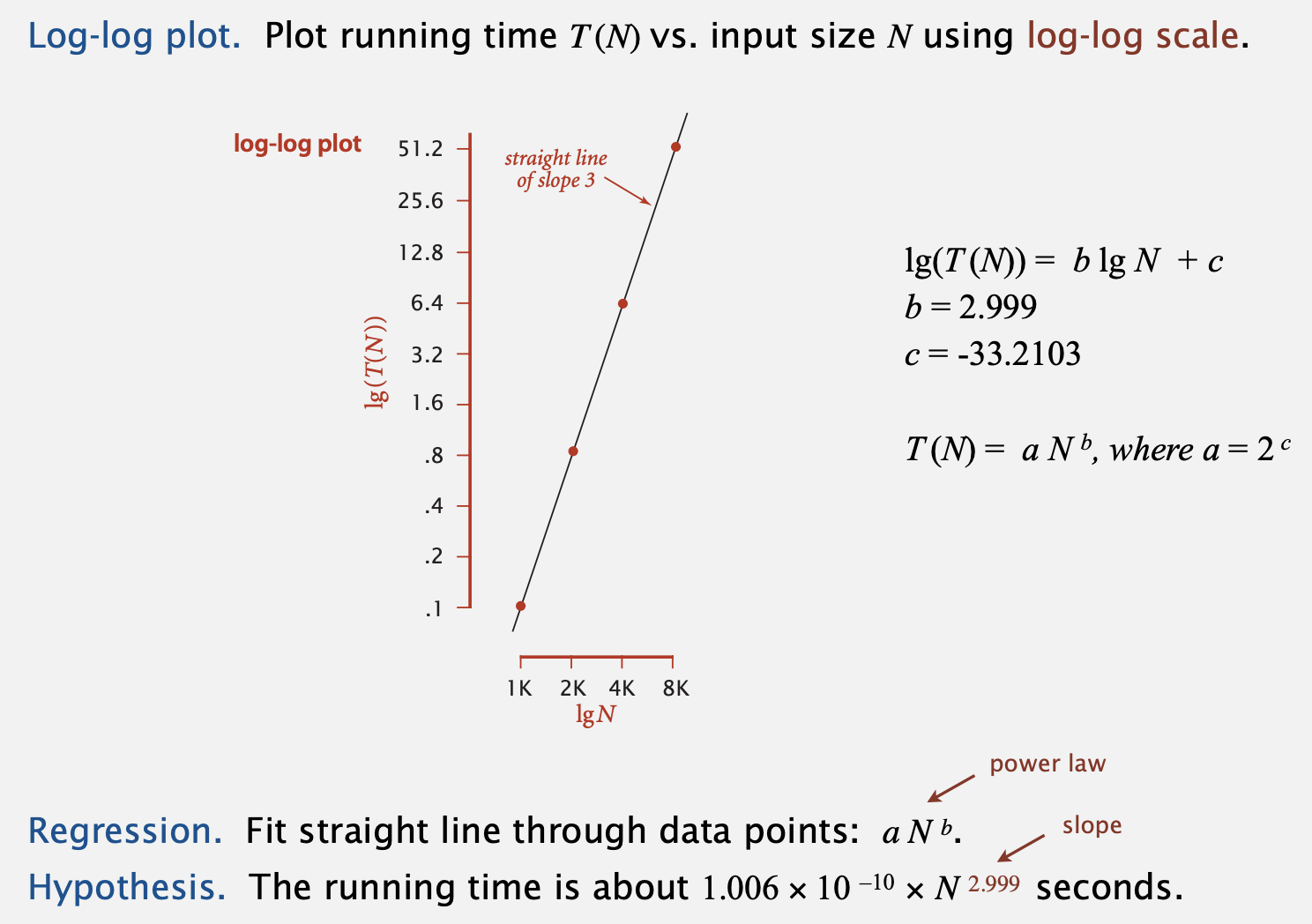
- 또다른 접근 방식으로는 input, output으로 그래프를 그려보는 것입니다.
이 경우엔 log-log scale로 그래프를 그리면서 복잡도를 계산해 볼 수 있죠. - 여기서 b는 몇 제곱, a는 배율에 관한 것이라고 생각하면 쉽습니다.
이를 테면 input이 증가함에 따라 얼마나 큰 폭으로 제곱이 되는가가 b로 표현되고,
그 결과물에 얼마를 곱해야 되는지는 a로 표현되는 것이죠.
(마지막 퀴즈에 추가 설명이 있습니다)
Prediction and validation


- 일정 수준으로 입력, 출력을 확인하다 보면 기울기가 확정됩니다.
상수로 고정이 되는 것이죠.
Experimental algorithmics
Quiz
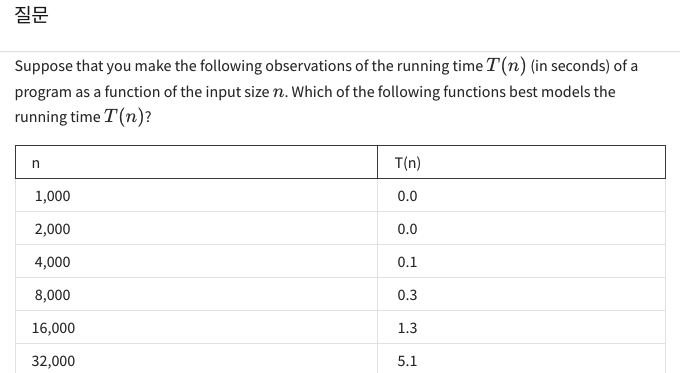

- 우리는 효율성을 log-log 스케일의 그래프를 통해 파악할 수 있다고 했습니다.
여기서는 T(n) = a * n^b 으로 표현됩니다. - n이 두 배 증가할 때, T(n)은 약 네 배 증가하는 것을 알 수 있죠.
즉 n = 1, 2, 4, 8, ... 이라면 T(n) = 1, 4, 16, 64 ... 꼴입니다.
따라서 n의 몇 제곱인지를 나타내는 b의 값이 2라는 것을 알 수 있습니다. - 따라서 n = 64000, T(64000) = 20.5인 상황을 예로 들 경우,
이 값을 64000의 제곱으로 나눠보면 a x 10^-9가 되고 이때의 a가 5.0으로 구해집니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(4) : Order-of-Growth Classifications (0) | 2023.04.03 |
|---|---|
| Analysis of Algorithms(3) : Mathematical Models (0) | 2023.04.02 |
| Analysis of Algorithms(1) : Analysis of Algorithms Introduction (0) | 2023.04.02 |
| Union-Find(5) : Union-Find Applications (0) | 2023.04.01 |
| Union-Find(4) : Quick-Union Improvements (0) | 2023.04.01 |
Example: 3-Sum & brue-force algorithm


- 배열 내의 세 원소 합이 0이 되는 경우의 수를 구하는 알고리즘입니다.
- 생각이 필요 없는 아주 단순한 풀이 방식을 생각하면 brute force 방식을 떠올릴 수 있을 것입니다.
- 이때 i, j, k가 원소의 개수 n만큼 탐색하는 방식입니다.
- 따라서 시간 복잡도는 무려 O(N^3)으로 엄청나게 비효율적입니다.
Measuring the running time


- 나의 알고리즘이 작동하는데 얼마만큼의 시간이 소요되는지 측정하는 방법은 다양하겠지만...
직접 스톱워치를 재는 경우는 없겠죠? - 대부분은 저런 코드를 사용해서 실행 시간을 측정하곤 합니다.
파이썬에도 time 모듈이 있어서 알고리즘의 효율성을 판단할 수 있습니다.
Empirical & Data analysis



- 또다른 접근 방식으로는 input, output으로 그래프를 그려보는 것입니다.
이 경우엔 log-log scale로 그래프를 그리면서 복잡도를 계산해 볼 수 있죠. - 여기서 b는 몇 제곱, a는 배율에 관한 것이라고 생각하면 쉽습니다.
이를 테면 input이 증가함에 따라 얼마나 큰 폭으로 제곱이 되는가가 b로 표현되고,
그 결과물에 얼마를 곱해야 되는지는 a로 표현되는 것이죠.
(마지막 퀴즈에 추가 설명이 있습니다)
Prediction and validation


- 일정 수준으로 입력, 출력을 확인하다 보면 기울기가 확정됩니다.
상수로 고정이 되는 것이죠.
Experimental algorithmics

Quiz


- 우리는 효율성을 log-log 스케일의 그래프를 통해 파악할 수 있다고 했습니다.
여기서는 T(n) = a * n^b 으로 표현됩니다. - n이 두 배 증가할 때, T(n)은 약 네 배 증가하는 것을 알 수 있죠.
즉 n = 1, 2, 4, 8, ... 이라면 T(n) = 1, 4, 16, 64 ... 꼴입니다.
따라서 n의 몇 제곱인지를 나타내는 b의 값이 2라는 것을 알 수 있습니다. - 따라서 n = 64000, T(64000) = 20.5인 상황을 예로 들 경우,
이 값을 64000의 제곱으로 나눠보면 a x 10^-9가 되고 이때의 a가 5.0으로 구해집니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(4) : Order-of-Growth Classifications (0) | 2023.04.03 |
|---|---|
| Analysis of Algorithms(3) : Mathematical Models (0) | 2023.04.02 |
| Analysis of Algorithms(1) : Analysis of Algorithms Introduction (0) | 2023.04.02 |
| Union-Find(5) : Union-Find Applications (0) | 2023.04.01 |
| Union-Find(4) : Quick-Union Improvements (0) | 2023.04.01 |
