Mathematical models for running time

- 1970년대에 프로그램의 작업 효율을 확인할 수 있는 수학적 모델이 고안되었다고 합니다.
Cost of basic operations
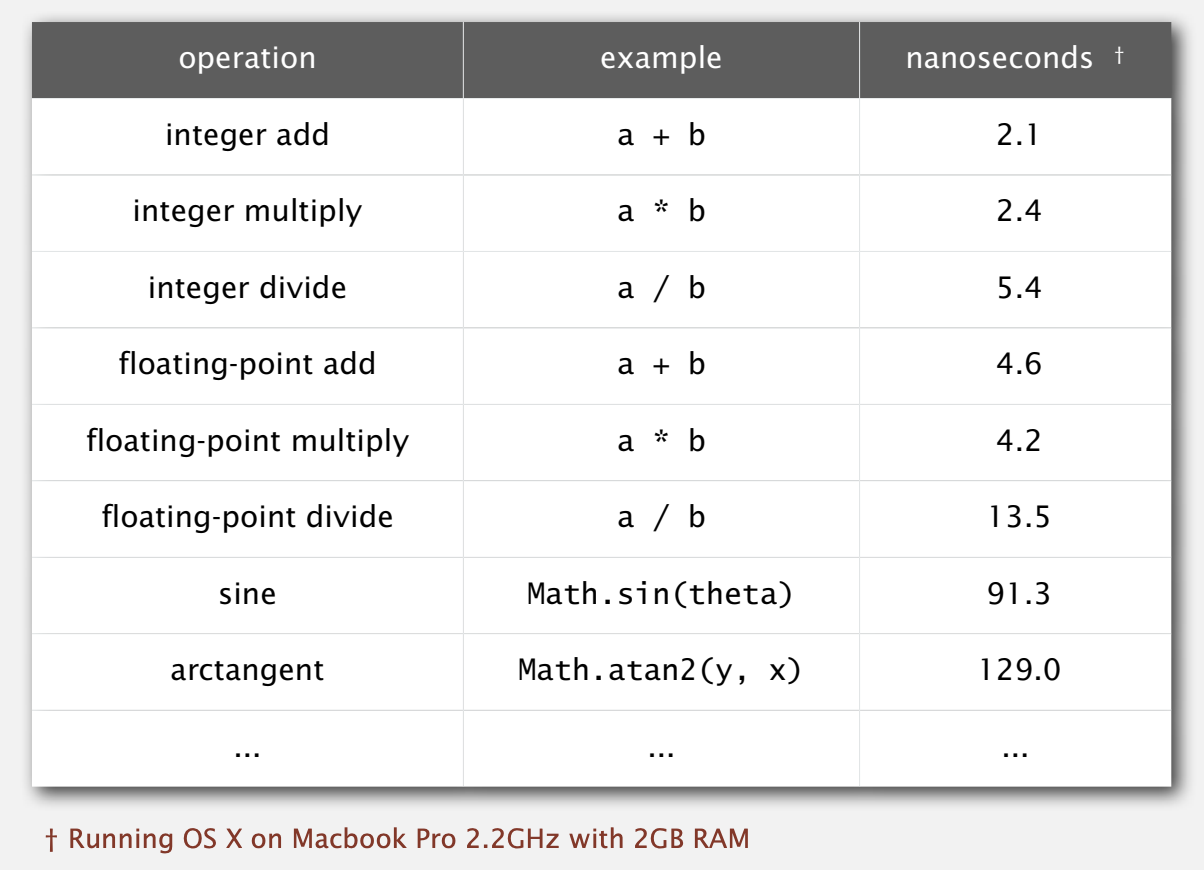
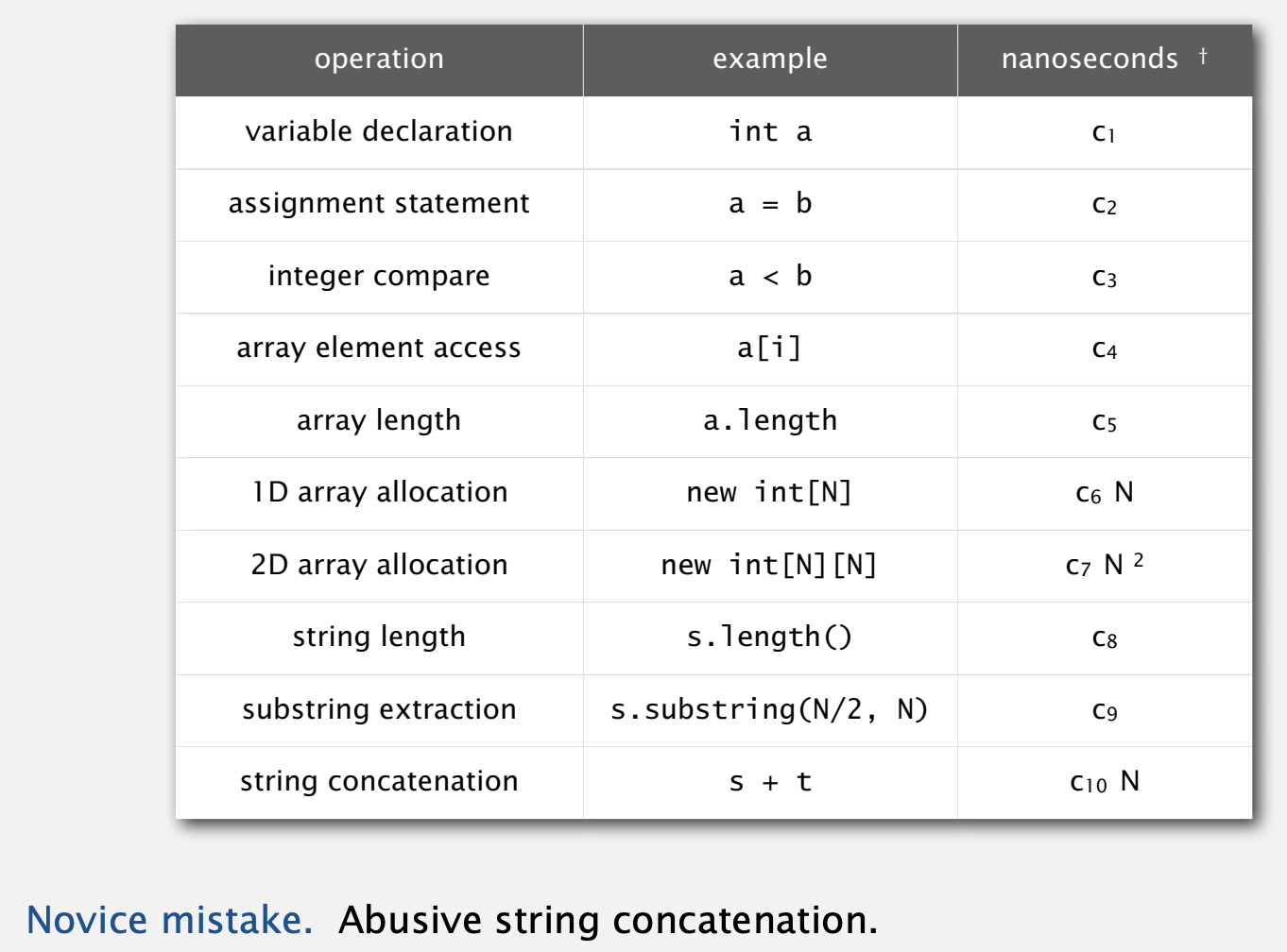
- 예전에는 이런 표를 참고해서 프로그램을 만들었다고 하네요..
기본 연산 명령을 수행하는데 걸리는 시간을 나노초 단위로 정리한 표입니다.
Example: 1-Sum, 2-Sum


- 1-Sum과 2-Sum을 예시로 실제 명령이 몇 번 수행되는지를 분석한 결과입니다.
- 모든 명령에 대해 굉장히 세부적으로 분석이 되어 있고, 딱 봐도 '귀찮아..'라는 느낌을 줍니다.
Simplifying the calculations

- 그래서 이러한 계산을 간단하게 정리하는 방법이 고안되었고 지금의 방식이 그걸 지켜오고 있는 거라고 생각하면 될 것 같습니다.
여러 연산들 중에서 '가장 빈도가 높은 것'만 고려하는 것입니다.
Simplification 1: cost model

- 그니까 이 예시에서는 배열에 접근하는 것이 N(N-1)로 빈도가 가장 높으므로 이 알고리즘의 복잡도를 이것 하나로 표현하는 것이죠.
Simplification 2: tilde notation

- 표기 자체도 간단하게 변경합니다.
가장 영향을 많이 주는, 즉 연산이 가장 많이 수행되는 항만 고려해서 표기하는 것이죠.
Example: 2-Sum & 3-Sum


- 위에서 설명한대로 시간 복잡도를 간단하게 표현한 것을 알 수 있습니다.
Estimating a discrete sum

- 덧셈 연산에 필요한 시간을 계산하는 식들을 정리한 것입니다.
- 시그마(덧셈)로 표현되던 것을 인테그랄(적분)으로 변경하며 구한 면적으로 복잡도를 계산합니다.
Mathematical models for running time

- 실질적으로 계산을 직접 하는 것은 상당히 어렵고 전문가의 영역이 될 수 있는데, 그렇기 때문에 우리는 근사치를 구하는 수준의 수학적 모델만 이용해도 충분하다고 설명합니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(5) : Theory of Algorithms (0) | 2023.04.03 |
|---|---|
| Analysis of Algorithms(4) : Order-of-Growth Classifications (0) | 2023.04.03 |
| Analysis of Algorithms(2) : Observations (0) | 2023.04.02 |
| Analysis of Algorithms(1) : Analysis of Algorithms Introduction (0) | 2023.04.02 |
| Union-Find(5) : Union-Find Applications (0) | 2023.04.01 |
Mathematical models for running time

- 1970년대에 프로그램의 작업 효율을 확인할 수 있는 수학적 모델이 고안되었다고 합니다.
Cost of basic operations


- 예전에는 이런 표를 참고해서 프로그램을 만들었다고 하네요..
기본 연산 명령을 수행하는데 걸리는 시간을 나노초 단위로 정리한 표입니다.
Example: 1-Sum, 2-Sum


- 1-Sum과 2-Sum을 예시로 실제 명령이 몇 번 수행되는지를 분석한 결과입니다.
- 모든 명령에 대해 굉장히 세부적으로 분석이 되어 있고, 딱 봐도 '귀찮아..'라는 느낌을 줍니다.
Simplifying the calculations

- 그래서 이러한 계산을 간단하게 정리하는 방법이 고안되었고 지금의 방식이 그걸 지켜오고 있는 거라고 생각하면 될 것 같습니다.
여러 연산들 중에서 '가장 빈도가 높은 것'만 고려하는 것입니다.
Simplification 1: cost model

- 그니까 이 예시에서는 배열에 접근하는 것이 N(N-1)로 빈도가 가장 높으므로 이 알고리즘의 복잡도를 이것 하나로 표현하는 것이죠.
Simplification 2: tilde notation

- 표기 자체도 간단하게 변경합니다.
가장 영향을 많이 주는, 즉 연산이 가장 많이 수행되는 항만 고려해서 표기하는 것이죠.
Example: 2-Sum & 3-Sum


- 위에서 설명한대로 시간 복잡도를 간단하게 표현한 것을 알 수 있습니다.
Estimating a discrete sum

- 덧셈 연산에 필요한 시간을 계산하는 식들을 정리한 것입니다.
- 시그마(덧셈)로 표현되던 것을 인테그랄(적분)으로 변경하며 구한 면적으로 복잡도를 계산합니다.
Mathematical models for running time

- 실질적으로 계산을 직접 하는 것은 상당히 어렵고 전문가의 영역이 될 수 있는데, 그렇기 때문에 우리는 근사치를 구하는 수준의 수학적 모델만 이용해도 충분하다고 설명합니다.
출처: Coursera, Algorithms, Part 1, Princeton University
'Algorithms, Part 1 > 1주차' 카테고리의 다른 글
| Analysis of Algorithms(5) : Theory of Algorithms (0) | 2023.04.03 |
|---|---|
| Analysis of Algorithms(4) : Order-of-Growth Classifications (0) | 2023.04.03 |
| Analysis of Algorithms(2) : Observations (0) | 2023.04.02 |
| Analysis of Algorithms(1) : Analysis of Algorithms Introduction (0) | 2023.04.02 |
| Union-Find(5) : Union-Find Applications (0) | 2023.04.01 |
