4.4.1. 변수변환
우선은 구체적인 예
- x1, x2에 대한 식을 y1, y2로 치환하여 재배치

- 따라서 x1, x2도 폭주한다.
행렬로 바꿔 말하면
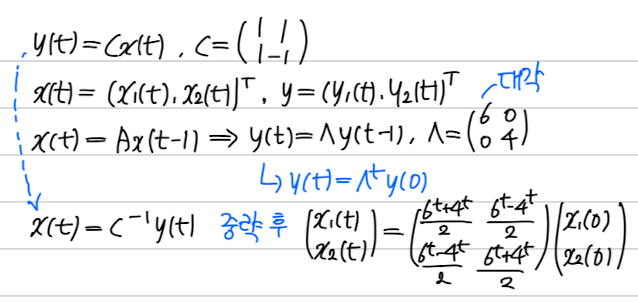
일반화
1. 힌트로 주어진 행렬 C를 사용하여 변수 x(t)를 다른 변수 y(t) = Cx(t)로 변환한다.
2. x(t) 식으로 주어진 차분방정식을 y(t) 식으로 다시 쓴다.
3. 고쳐 쓴 식은 '대각 행렬'이 된다.
4. 풀어서 얻은 y(t)를 x(t)로 되돌리면 답이다.
- x와 y가 일대일 대응할 수 있도록 C는 정칙행렬로 가정한다.

- 대각화하는 방법은 한 가지다.
4.4.2. 좋은 변환을 구하는 방법
- 대부분의 정방행렬 A에 대해 P^-1AP는 대부분 대각행렬이 된다.

좋은 P를 구하기 위해서는
1. A의 고윳값에 대응하는 고유벡터를 구한다.
2. 고유벡터를 나열하여 P = (p1, ... , pn)으로 둔다.
- 이때 P는 반드시 정칙이어야 한다.
- 고윳값, 고유벡터를 구하면 폭주 여부를 판정할 수 있다.
4.4.3. 좌표변환으로서의 해석

- 이때도 마찬가지로 P가 정칙인지 확실히 확인해야 한다.
4.4.4. 거듭제곱으로서의 해석
x(t) = A'x(0)에 대해
- A가 대각인 경우

- A가 대각이 아닌 경우

4.4.5. 결론: 고윳값의 절댓값 나름

출처: 히라오카 카즈유키, 호리 겐, 『프로그래머를 위한 선형대수』, 이창신, 길벗, 2017.
'프로그래머를 위한 선형대수 > 4장' 카테고리의 다른 글
| 4.7. 대각화할 수 없는 경우 (0) | 2022.09.17 |
|---|---|
| 4.6. 연속시간 시스템 (0) | 2022.09.15 |
| 4.5. 고윳값, 고유벡터 (0) | 2022.09.15 |
| 4.2. 1차원의 경우 / 4.3. 대각행렬의 경우 (0) | 2022.09.14 |
| 4.1. 문제 설정: 안정성 (0) | 2022.09.13 |
