
- 연속시간 시스템에 대해서도 폭주를 판정해야 한다.
4.6.1. 미분방정식
미분방정식
- 미지의 함수와 그 미분을 포함하는 등식을 보고, 이 등식이 성립하는 함수를 답하는 것
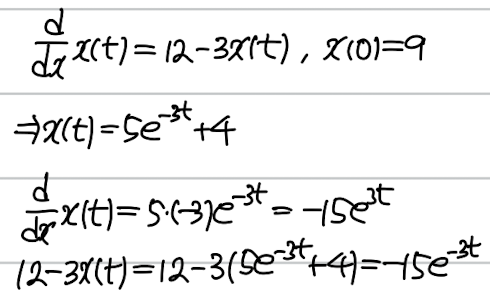
- 하나의 변수 t의 함수 x(t)에 대한 방정식인 것을 강조하는 경우
- 편미분방정식과 대비한 호칭
4.6.2. 1차원일 때
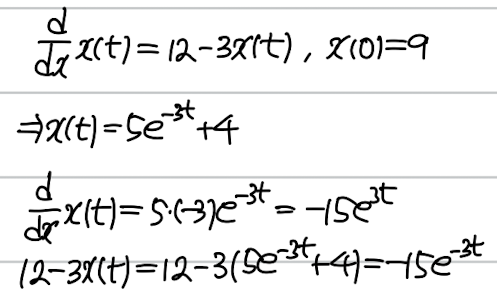
4.6.3. 대각행렬일 때
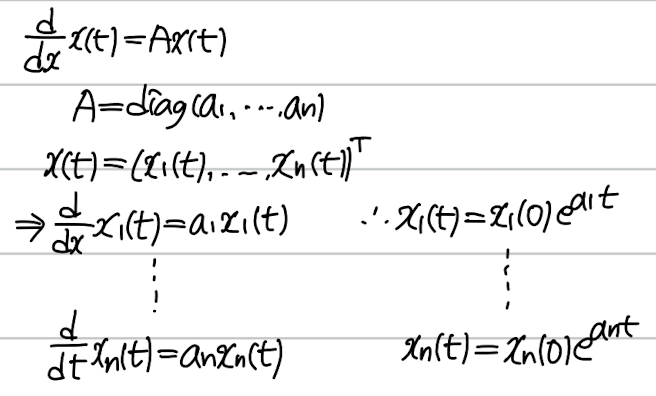
- a1, ... , an 중 하나라도 양수라면 폭주, 그렇지 않다면 폭주하지 않는다.
- 단, 이는 ai가 복소수가 아닐 때만 해당한다.
4.6.4. 대각화할 수 있는 경우

- 이 변환법은 이산시간의 경우와 동일하다.
4.6.5. 결론: 고윳값(실수부)의 부호

출처: 히라오카 카즈유키, 호리 겐, 『프로그래머를 위한 선형대수』, 이창신, 길벗, 2017.
'프로그래머를 위한 선형대수 > 4장' 카테고리의 다른 글
| 4.7. 대각화할 수 없는 경우 (0) | 2022.09.17 |
|---|---|
| 4.5. 고윳값, 고유벡터 (0) | 2022.09.15 |
| 4.4. 대각화할 수 있는 경우 (0) | 2022.09.15 |
| 4.2. 1차원의 경우 / 4.3. 대각행렬의 경우 (0) | 2022.09.14 |
| 4.1. 문제 설정: 안정성 (0) | 2022.09.13 |

- 연속시간 시스템에 대해서도 폭주를 판정해야 한다.
4.6.1. 미분방정식
미분방정식
- 미지의 함수와 그 미분을 포함하는 등식을 보고, 이 등식이 성립하는 함수를 답하는 것
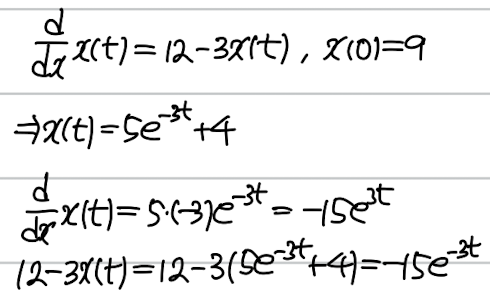
- 하나의 변수 t의 함수 x(t)에 대한 방정식인 것을 강조하는 경우
- 편미분방정식과 대비한 호칭
4.6.2. 1차원일 때
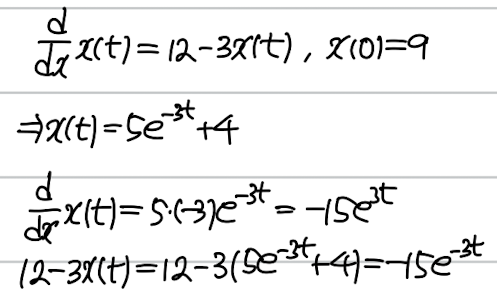
4.6.3. 대각행렬일 때
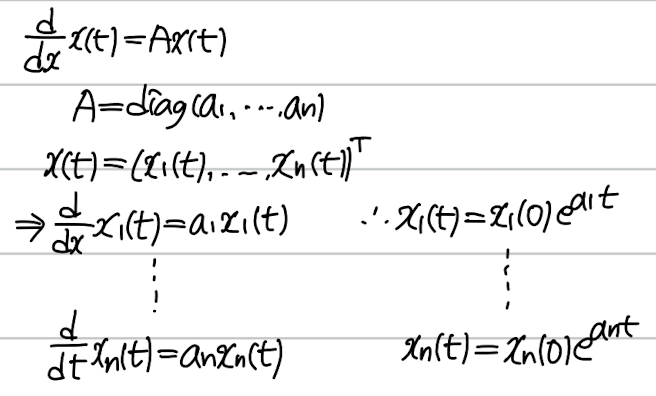
- a1, ... , an 중 하나라도 양수라면 폭주, 그렇지 않다면 폭주하지 않는다.
- 단, 이는 ai가 복소수가 아닐 때만 해당한다.
4.6.4. 대각화할 수 있는 경우

- 이 변환법은 이산시간의 경우와 동일하다.
4.6.5. 결론: 고윳값(실수부)의 부호

출처: 히라오카 카즈유키, 호리 겐, 『프로그래머를 위한 선형대수』, 이창신, 길벗, 2017.
'프로그래머를 위한 선형대수 > 4장' 카테고리의 다른 글
| 4.7. 대각화할 수 없는 경우 (0) | 2022.09.17 |
|---|---|
| 4.5. 고윳값, 고유벡터 (0) | 2022.09.15 |
| 4.4. 대각화할 수 있는 경우 (0) | 2022.09.15 |
| 4.2. 1차원의 경우 / 4.3. 대각행렬의 경우 (0) | 2022.09.14 |
| 4.1. 문제 설정: 안정성 (0) | 2022.09.13 |
