1. Matrices changing basis

- 검정색은 나의 기저벡터를, 파란색은 곰돌이의 기저벡터를 의미한다.
- 곰돌이의 기준을 나의 기준으로 표현하거나 그 반대를 시도한다.

- 곰돌이의 벡터를 나의 좌표계에서 표현하고, 곰돌이 좌표계 기준의 벡터 하나를 곱한다.
- 그 결과는 나의 기준으로 표현된다.
- 이 결과에 역행렬을 곱해주면 곰돌이의 벡터를 기준으로 위치가 표현된다.
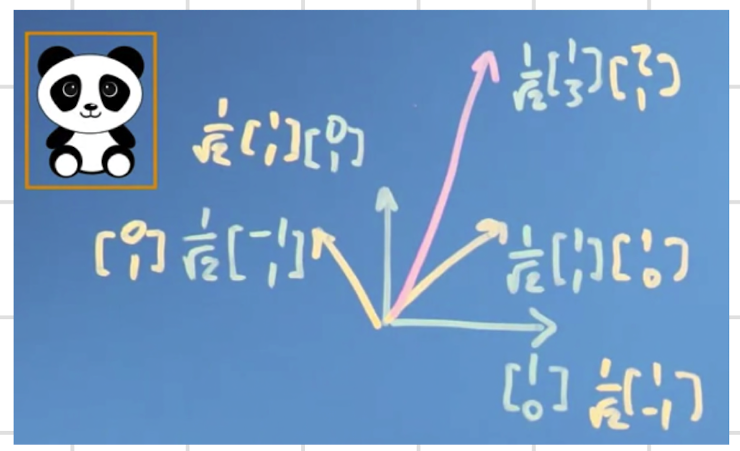
- 곰돌이와 나의 기저 벡터를 표현한 또 다른 예

- 위에서 확인했던 것처럼 곰돌이의 한 좌표를 나의 벡터를 기준으로 곱해주면 내 기준의 위치 표현이 된다.
- 이를 거꾸로 하는 과정은 역행렬을 통해 수행한다.
- 단, 곰돌이의 기저벡터가 서로 직교(orthogonal to each other)하는 경우, 내적을 통해 구할 수 있다.
2. Doing a transformation in a changed basis

- 곰돌이 기준의 회전을 어떻게 나의 기준으로 표현할 수 있는가?
- 내 기준 회전 행렬 R과 내 기준 B의 기저를 곱해 내 기준 회전을 표현한다.
- 여기에 B의 역행렬을 곱해줌으로써 곰돌이의 기준에서 회전을 표현한다.
출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
'Linear Algebra > 4주차' 카테고리의 다른 글
1. Matrices changing basis

- 검정색은 나의 기저벡터를, 파란색은 곰돌이의 기저벡터를 의미한다.
- 곰돌이의 기준을 나의 기준으로 표현하거나 그 반대를 시도한다.

- 곰돌이의 벡터를 나의 좌표계에서 표현하고, 곰돌이 좌표계 기준의 벡터 하나를 곱한다.
- 그 결과는 나의 기준으로 표현된다.
- 이 결과에 역행렬을 곱해주면 곰돌이의 벡터를 기준으로 위치가 표현된다.

- 곰돌이와 나의 기저 벡터를 표현한 또 다른 예

- 위에서 확인했던 것처럼 곰돌이의 한 좌표를 나의 벡터를 기준으로 곱해주면 내 기준의 위치 표현이 된다.
- 이를 거꾸로 하는 과정은 역행렬을 통해 수행한다.
- 단, 곰돌이의 기저벡터가 서로 직교(orthogonal to each other)하는 경우, 내적을 통해 구할 수 있다.
2. Doing a transformation in a changed basis

- 곰돌이 기준의 회전을 어떻게 나의 기준으로 표현할 수 있는가?
- 내 기준 회전 행렬 R과 내 기준 B의 기저를 곱해 내 기준 회전을 표현한다.
- 여기에 B의 역행렬을 곱해줌으로써 곰돌이의 기준에서 회전을 표현한다.
출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
