1. The Gram-Schmidt process

- 선형독립인지 확인하고 싶으면 행렬식이 0인지 아닌지를 구해볼 것
- 위와 같은 방식으로 n개의 벡터를 정규화 하면 된다.
- 주어진 벡터를 이용해서 서로 수직인 벡터들을 만드는 방법이다.
- 현재 벡터와 여기에 이전 벡터들과 수직인 사영 벡터를 전부 빼주면 된다.
2. Gram-Schmidt process
- 그람 슈미츠 직교화를 주피터 노트북으로 구현하는 문제
- 빈칸을 채우는 방식으로 그렇게 어렵지는 않다
3. Example: Reflecting in a plane

- v1, v2는 평면을 구성하는 벡터, v3는 그 밖의 벡터이다.
- 그람-슈미트 직교화를 통해 기저 벡터 E를 구한다.

- e3에 대해 대칭인 위치를 찾고자 하는 것이므로 다른 벡터 두 개는 그대로, e3는 음수로 취한다.
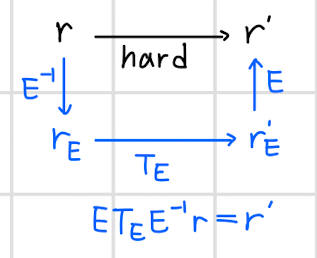
- r이라는 벡터에서 r'을 직접구하기가 어려우므로 위와 같은 과정을 거쳐 다을 구한다.
4. Relecting Bear
- 평면을 기준으로 반사되는 이미지의 위치를 찾는 과제
- 강의에서는 3차원을 기준으로 설명했으나 실제 코드를 작성할 때는 2차원을 기준으로 풀이하게 됨

출처: Coursera, Mathematics for Machine Learning: Linear Algebra, Imperial College London
'Linear Algebra > 4주차' 카테고리의 다른 글
| Making Multiple Mappings, deciding if these are reversible (0) | 2022.09.18 |
|---|---|
| Matrices transform into the new basis vector set (0) | 2022.09.18 |
| Matrices as objects that map one vector onto another; all the types of matrices (0) | 2022.09.18 |
