![]()
5.2.1. 평면 회전 전치행렬이 곧 역행렬이 된다. 5.2.2. 평면 회전에 의한 닮은변환 야코비법 이를 반복시행하면서 대각행렬에 다가가는 알고리즘 f(A)가 0으로 향한다는 것은 A가 대각행렬로 향한다는 것을 의미한다. 5.2.3. 계산 공부 이를 토대로 sin 값도 구할 수 있다. 출처: 히라오카 카즈유키, 호리 겐, 『프로그래머를 위한 선형대수』, 이창신, 길벗, 2017.
5.1.1. 손 계산과 차이점 특성방정식의 랭크를 정밀하게 구하는 것 자체가 어렵다 P^-1AP = 대각행렬 또는 상삼각행렬 꼴로 변형한다. 우변 행렬의 대각성분이 고윳값이 된다. 이 경우 고차랭크방정식을 푸는 과정을 생략할 수 있다. 5.1.2. 갈루아 이론 5차 미만의 대수방정식에는 해의 공식이 존재한다. 5차 이상의 대수방정식에는 해의 공식이 존재하지 않는다. 해를 구하는 절차가 존재하다면 이를 공식으로 만들 수 있다는 뜻이다. 하지만 공식의 형태로 나타내는 것이 지나치게 복잡하면 그렇게 하지 않는다. 예를 들어 3,4차 방정식에 대해서는 절차로만 나타낸다. 5.1.3. 5x5 이상 행렬의 고윳값을 구하는 순서는 존재하지 않는다! 5차 이상의 대수방정식을 푸는 순서가 존재하지 않으므로 위 진술이 자..
![]()
4.7.1. 먼저 결론 폭주 판정의 결론은 거의 변하지 않는다. 단, 특수한 경우 미묘한 문제가 발생한다. 4.7.2. 대각까지는 못하더라도 - 요르단표준형 대각화할 수 없는 정방행렬 A라도 대각에 가까운 요르단 표준형이라면 반드시 변환할 수 있다. 블록대각(블록정방행렬이고, 대각블록 이외는 모두 0) 대각블록의 성질 대각성분에 같은 수가 나열 하나 오른쪽 위는 1이 비스듬히 늘어섬 위와 같은 것을 요르단 셀이라고 한다. 여기서는 크기 5, 2, 1, 3 짜리 요르단 셀이 늘어서 있다. 행렬 A를 변환하여 만들 수 있는 요르단 표준형은 한 가지이다. 4.7.3. 요르단 표준형의 성질 폭주 판정과 관련이 있다. 고윳값, 고유벡터의 모양이 보인다. 거듭제곱을 구체적으로 계산할 수 있다. 요르단 표준형의 고윳..
![]()
1. Determinants and inverses Determinant 공간이 얼마나 넓어졌는지를 나타내는 지표 2차원 기준 평행사다리꼴의 면적이 위 예시에 동일하다는 것을 확인할 수 있다. 즉, 행렬식이 같은 경우다. 2차원의 행렬식 구하기 2차원의 행렬식은 ad-bc 가 된다. 역행렬과 1 / 행렬식, 행렬을 곱하면 단위 행렬이 된다. 행렬식과 역행렬의 관계 행렬식이 0인 경우 역행렬은 존재하지 않는다. 행렬식이 0이라는 것은 어떤 문제를 풀기에 정보가 불충분하다는 것을 의미하기 때문이다. 따라서 기약행 사다리꼴을 만들었을 때, 각 열벡터가 선형 독립이어야만 필요한 정보를 모두 갖추고 있는 것으로 이해할 수 있다. 여기서 선형 독립은, 어떤 열벡터를 다른 열벡터들의 연산을 통해 얻지 못한다는 것을 ..
![]()
1. Solving the apples and bananas problem: Gaussian elimination Inverses: solving the apples and bananas problems and Gaussian Elimination 역행렬이란? 문제를 간단하게 풀 수 있게 만들어 준다. 가우스 소거법(예시) 제거와 후치환 방식을 적용하여 위 같은 행렬을 구할 수 있다. 주대각선은 전부 1이고, 나머지는 전부 0인 행렬이다. 이런 행렬을 echelon form(사다리꼴)이라고 한다. 2. Going from Gaussian elimination to finding the inverse matrix 가우스 소거법을 이용하여 역행렬을 구할 수 있다. 3. Solving linear equati..
![]()
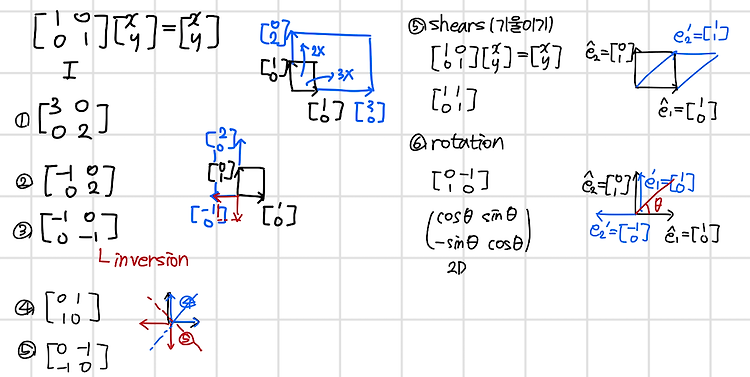
1. How matrices transform space 행렬의 곱을 단위벡터와의 곱으로 변환할 수 있다. 이때 분배법칙을 이용한다. 2. Types of matrix transformation possible sorts of changes we can do with a matrix 3. Composition or combination of matrix transformations 행렬의 곱은 순서를 다르게 하면 동일한 결과가 보장되지 않는다.(isn't commutative, 교환 법칙 x) 하지만 결합 법칙은 성립할 수 있다.(associative) 행렬의 곱은 변환에 변환을 적용한 것으로 이해할 수 있다. 4. Using matrices to make transformations(Quiz 6) 행렬..