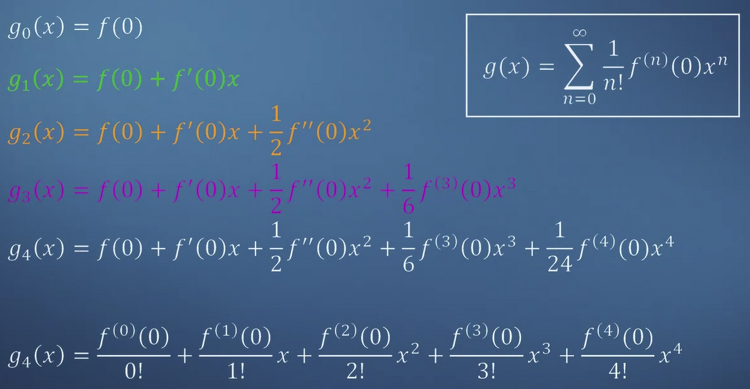테일러 급수

1. Power series details 기존과 달리 Taylor series에서는 x=0이 아닌 어떤 point에서 접근해도 상관 없다고 본다. 따라서 여기서는 x = p로 가정하고 접근한다. Taylor Series에서 p = 0을 대입하면 기존의 Maclaurin Series와 동일해지는 것을 확인할 수 있다. 위에 정리된 식처럼 만약 2차식을 미분하게 되면 미분 과정에서 계수 때문에 2!이 분모가 될 것임을 짐작 가능하다. 이 과정을 일반화한 것이 Taylor Series가 된다. 2. Applyting the Taylor series (Quiz) 여러 f(x)에 대해 x = 0(Maclaurin) 또는 x = p(Taylor) 의 근사 함수를 구하는 문제가 출제된다. 이를 위해서 분수함수의 미..

1. Building approximations 1) 이 cooking book을 읽는 사람과 내가 비슷한 오븐을 쓴다고 가정 2) 치킨도 비슷하다고 가정 다른 조건들이 유사하다고 가정하면 변수들을 줄일 수 있고 이를 통해 간단한 식으로 근사할 수 있게 된다. 2. Power series Truncated series 주어진 함수 g의 변수를 하나씩 늘려나가면서 기존의 그래프와 얼마나 유사한지 확인하고 있다. 변수를 늘릴수록 기존의 그래프와 유사해지는 것을 볼 수 있다. 이런 방식으로 쭉 늘어놓은 함수의 모음을 truncated series라고 부른다. 3. Matching functions and approximations (Quiz) 기존의 그래프를 보고 적절한 근사를 고르는 문제들이 출제되어 있다...