목차
1. Regularization
Logistic regression
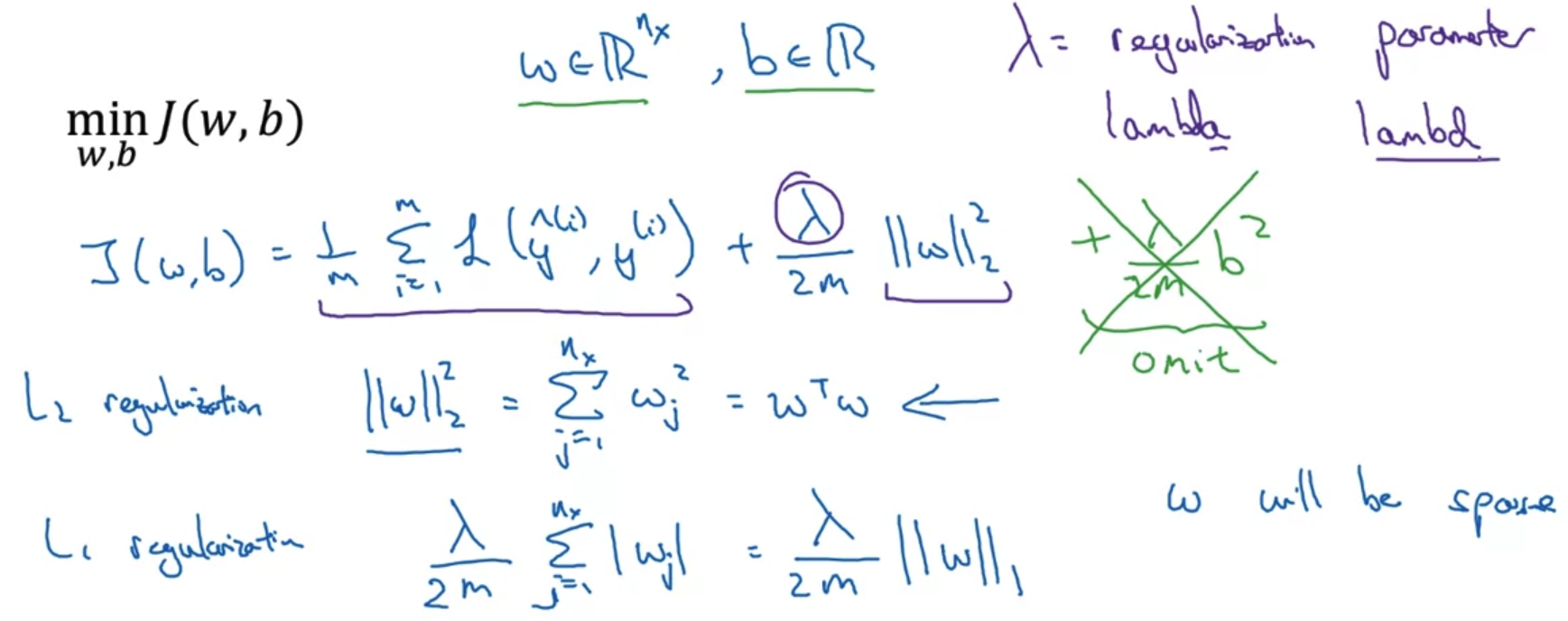
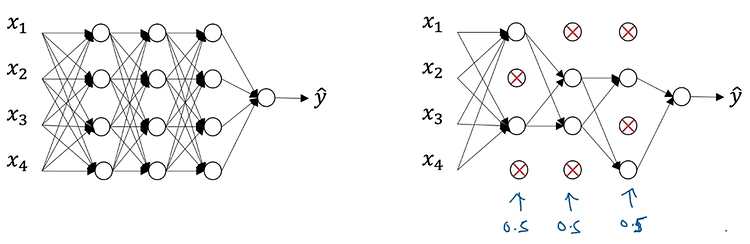
- High variance 문제가 있을 때 데이터를 늘리기 어려운 상황이라면 regularization을 적용할 수 있다.
loss function으로 구한 cost function J를 최소화하는 logistic regression을 예시로 들어 내용을 살펴보자. - 기존의 logistic regression에서는 J가 prediction과 target 간의 차이를 평균낸 것으로 정의된다.
여기에 lambda라는 일종의 hyper parameter와 전체의 개수 m으로 나눠준 값을 계수로 갖는 L2 norm을 곱한 값을 더해준다.
쉽게 말하면 '특정 계수와 L2 norm을 곱한 값의 평균'을 더해준다는 것이다. - 이때 두 변수 w와 b에 대해 모두 regularization을 적용할 필요는 없다.
왜냐하면 훨씬 더 많은 변수들을 포함하는 w와 달리 b는 하나의 값이므로 실제 over-fitting은 대부분 w의 변수들로 인해 발생하기 때문이다.
물론 원한다면 b에 대해서도 regularization을 적용할 수 있겠지만 큰 의미가 없을 가능성이 높다. - 뿐만 아니라 L1 regularization 방식도 존재한다.
이는 유클리언 방식으로 접근하는 L2와 달리 단순히 절댓값만을 구하는 방식으로,
이를 적용했을 때는 w가 이전에 비해 sparse한 형태를 띄게 만든다.
Neural network
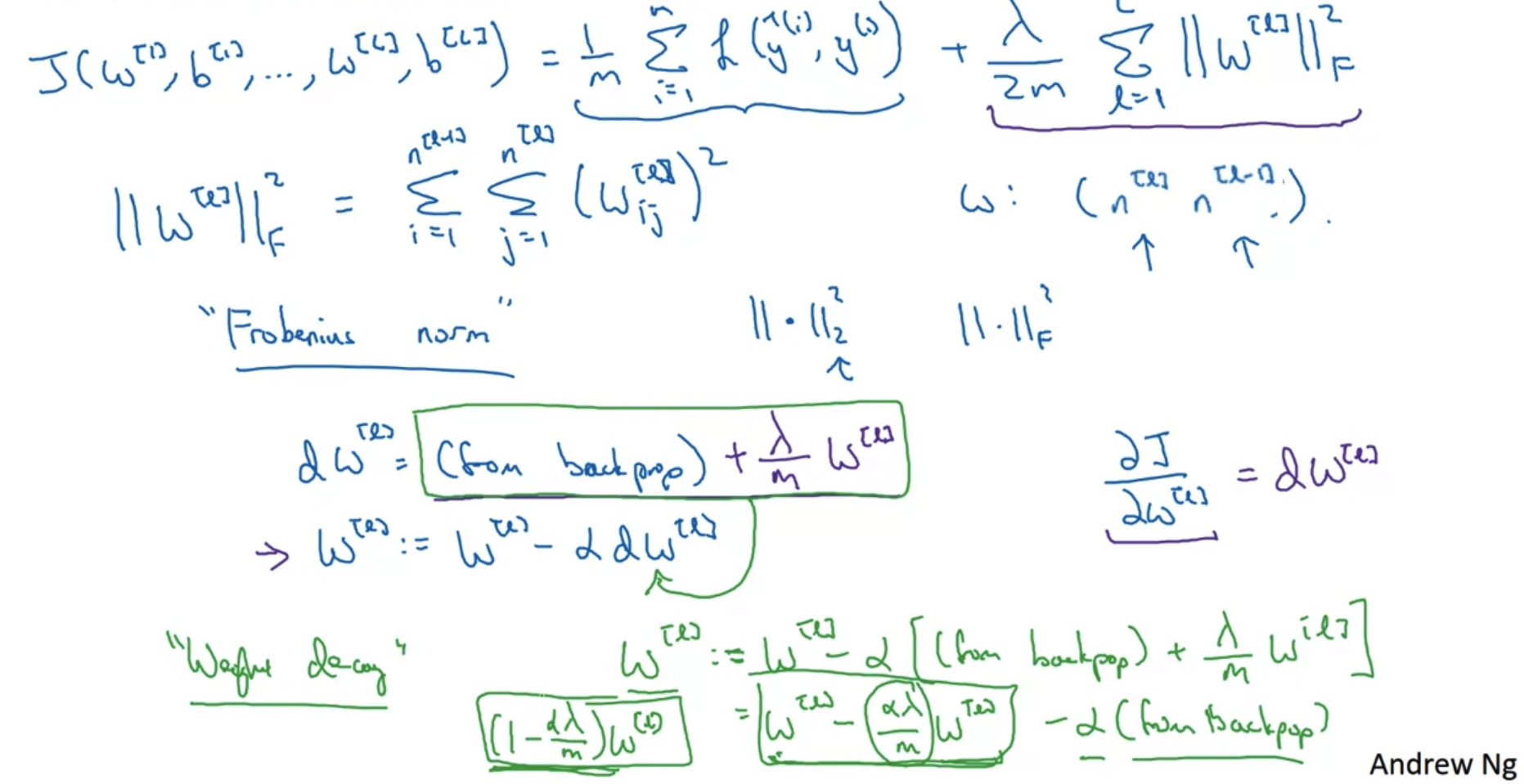
- Logistic regression의 문제를 neural network 문제로 확장시키면 어떻게 될까?
- 개념 자체는 동일하고 matrix로 확장된다는 점에만 유의하면 될 것이다.
- 이때 L2 norm으로 정의되는 부분을 여기서는 Frobenius norm이라고 부른다.
- Back-propagation에 의해 update되는 W를 자세히 살펴보자.
- 기존의 dw가 back-propagation에 의해 구해지는 결과였다면 여기에 Frobenius norm을 w에 대해 미분한 결과를 더해주어야 한다.
- w는 미분값을 alpha와 곱하여 빼줌으로써 업데이트 되는데 빼야하는 값이 커진다고 이해할 수 있다.
- Weight decay
- w가 변형된 dw를 빼면서 나온 결과를 잘 보면 기존의 가중치 w가 이전보다 줄어들었다는 것을 확인할 수 있다.
- 따라서 이런 식으로 L2 norm을 사용하여 regularization을 수행하는 것을 'weight decay'라고 부른다.
Frobenius norm을 보면 두 개의 시그마가 중첩되어 있는데 이때 i,j 범위가 바뀌어 있다.
i는 current layer, j는 previous layer의 숫자를 의미하기 때문에 두 범위를 바꿔주어야 한다.
2. Why Regularization Reduces overfitting?
How does regularization prevent overfitting?
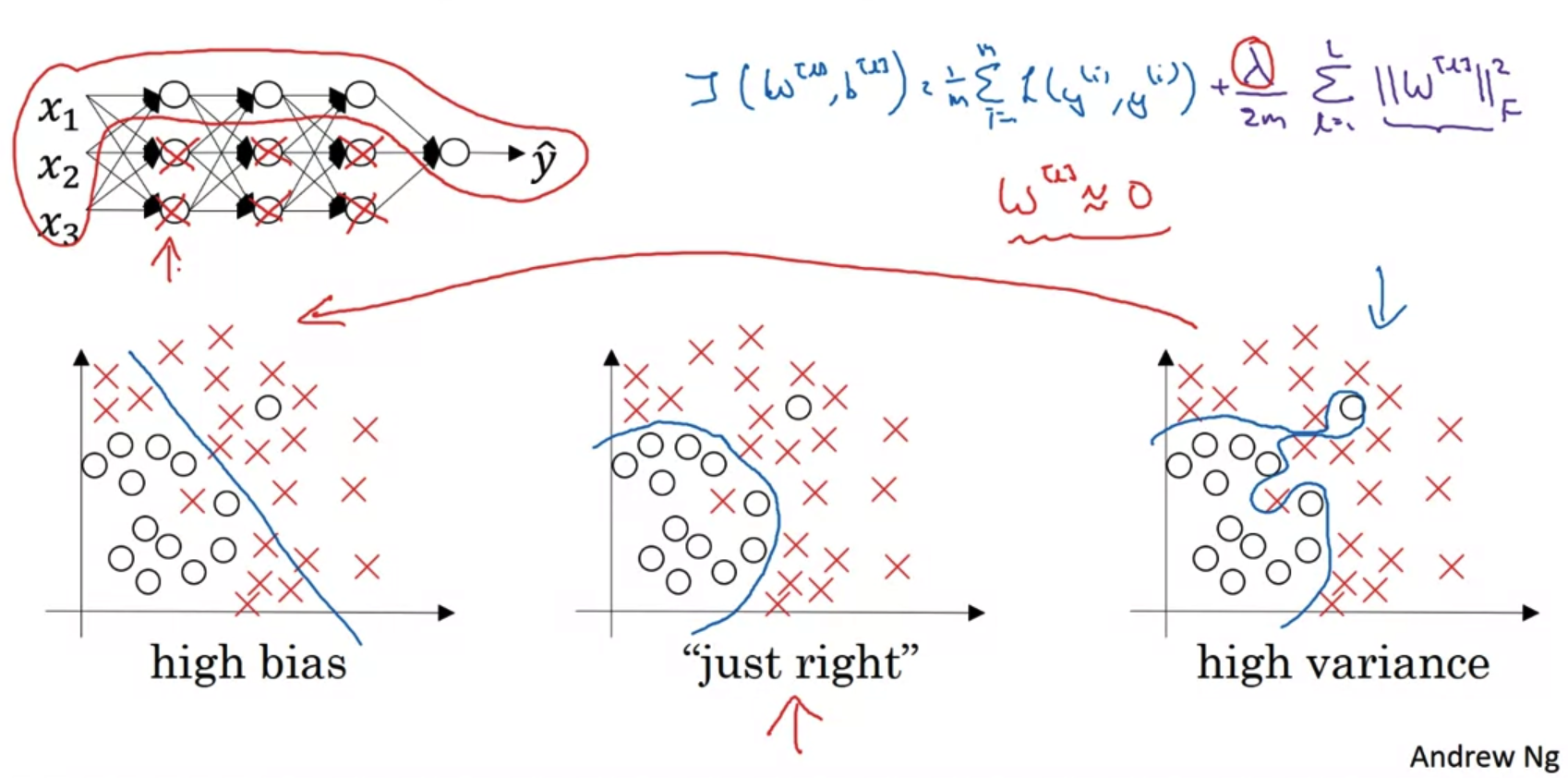
- 새롭게 정의된 Cost function J를 보자.
우리는 back-propagation 과정에서 w의 값을 dw를 빼면서 update해준다.
따라서 새로 정의된 J에 따르면 lambda가 커질수록, update에서 빼야하는 dw가 커지면서 w는 사실상 '0'이 될 것이다. - 그러면 그림의 왼쪽 위 도식처럼 neural network 내부의 끊어져 마치 logstic regression을 여러 layer를 거쳐 쌓은 것과 유사한 구조가 될 것이다.
결국 이것이 의미하는 바는 'w라는 가중치가 prediction에 미치는 영향이 대폭 줄어들었다'는 것이다. - 물론 실제로는 lambda의 값이 커지더라도 w가 0이 되는 것은 아니지만,
w의 값이 굉장히 작아짐으로 인해 over-fitting이 완화되는 효과를 볼 수 있다. - 직관적으로 이해해보자면 맨 우측의 high variance의 형태를 좌측의 high bias로 유도하여 중간의 'just right'의 형태로 만들고자 하는 것이다.
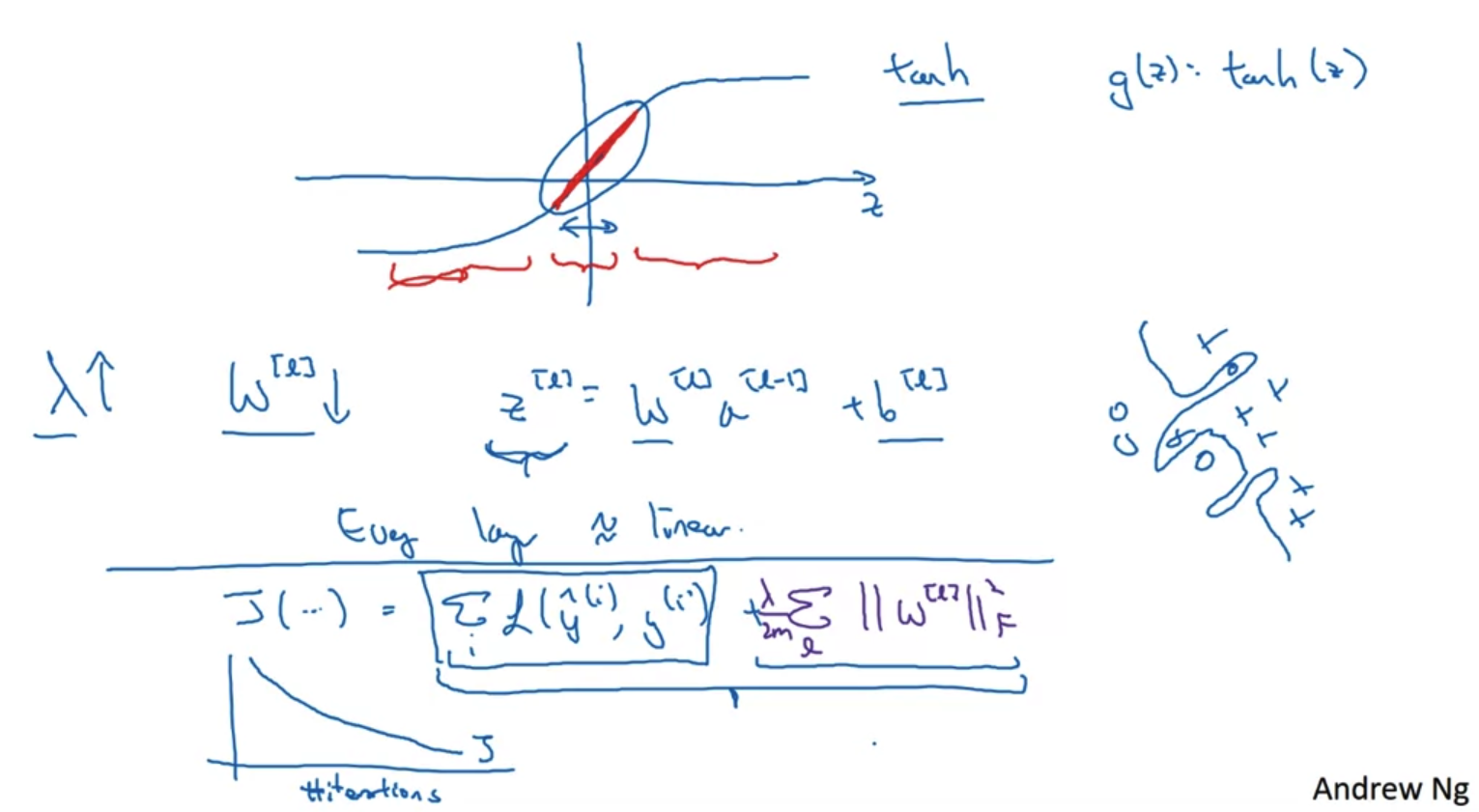
- 위 내용을 activation function 관점에서도 해석해 볼 수 있다.
- 만약 regularization의 parameter lambda의 값이 매우 커진다면 앞서 확인한 것처럼 w의 값이 줄어들 것이다.
그렇다면 가중치 w와 편향 b를 더해 구한 z의 값도 줄어들 것임을 알 수 있다.
정확히는 z 값의 범위(range)가 굉장히 작아진다. - z값을 tan h 함수의 변수로 이용하여 g라는 변수를 구한다는 점을 떠올려 보자.
z의 값이 굉장히 작아지게 된다면 tan h의 x축 범위가 굉장히 작다는 것을 의미한다.
따라서 그 y 값의 범위도 작아지는데, 결과적으로 linear한 형태로 결과물이 도출된다. - 이는 여러 층의 nerual network를 만들어 비선형 근사를 했던 것을 다소 linear하게 만들어 줌으로써 over-fitting을 완화하는 것으로 이해할 수 있게 된다.
- 추가로 새롭게 정의된 cost function으로 모델을 돌리며 반복한 것과 실제 cost의 값을 그래프로 표현해보면 regularization을 적용했을 때 cost가 monotonically 감소하는 것을 확인할 수 있을 것이다.
3. Dropout Regularization
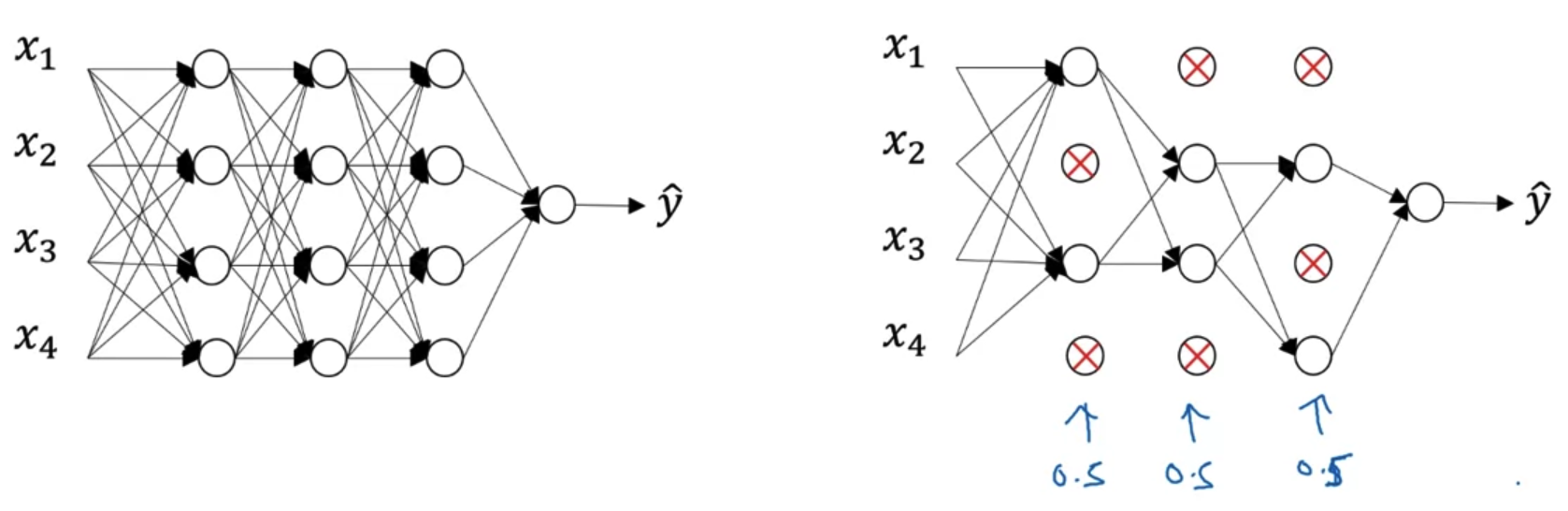
- Dropout은 over-fitting을 방지하기 위한 기법이다.
- 각 layer에 대해서 일정 확률로 연결을 끊고 학습을 진행한다.
결과적으로 더 작은 size의 neural network를 갖게 된다.
Implementing dropout("Inverted dropout")

- Dropout을 적용하는 방법은 위와 같다.(교수님의 손코딩..!)
layer가 3개인 network를 예시로 들어보자. - keep.prob은 기존 node를 유지할 비율을 뜻한다.
즉 이를 0.8로 설정하면 80%는 그대로 유지하고 20%는 shut off 하겠다는 것을 의미한다.
이 비율을 기준으로 a3의 shape을 딴 d3을 구해준다. - 이제 0과 1로 구성된(80%는 1, 20%는 0) d3을 a3과 곱해준다.
이때는 element-wise 연산을 수행하는 것이다. - dropout을 통해 a3에 포함되는 노드의 20%를 날려주고 나면 a3의 남은 80% 노드를 keep_prob = 0.8로 나눠야 한다.
이는 기존의 데이터 양을 보존하기 위함인데 예를 통해 알아보도록 하자.
기존 a3 노드가 100개라고 가정하자.(각 노드는 크기가 1이라고 생각한다)
만약 kee_prob = 0.8로 설정하여 dropout을 적용하면 80개의 노드가 남고 20개는 사라진다.
즉, 80개의 노드는 기존의 값을 유지하고 나머지 20개는 0이 되는 것이다.
결과적으로 처음에는 100만큼의 데이터가 있었지만 dropout을 적용함으로써 80만큼의 데이터만 남게 된다.
forward를 수행하는 과정에 있어서 데이터의 크기가 줄어든다면 layer가 여러 개인 network의 경우 데이터의 크기가 0에 수렴할 것이다.
결국 어떤 것도 학습하지 않게 되는 문제가 발생한다.
이를 해결하기 위해 80만큼의 남은 데이터를 0.8로 다시 나눠준다.
그러면 80 / 0.8 = 100 이므로 기존의 데이터 크기를 유지할 수 있게 된다.
즉, 기존의 데이터 크기를 유지하기 위해 dropout이 적용되는 각 layer마다 유지 비율(1-dropout 비율)로 나눠줌으로써 데이터의 크기를 보존하는 것이다.
Making predictions at test time
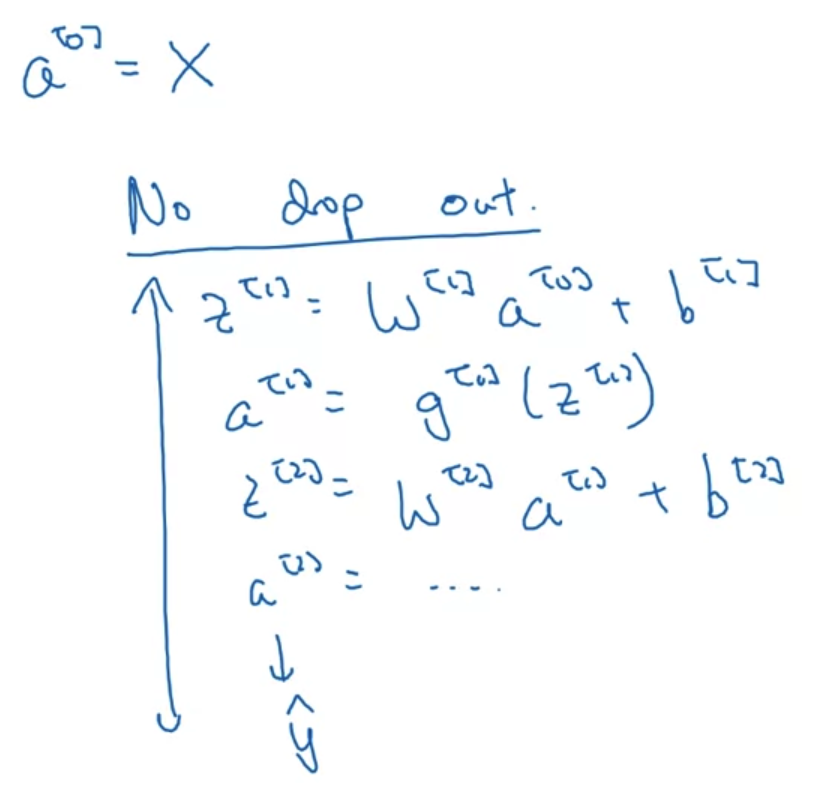
- test 할 때는 dropout을 적용하지 않는다.
- dropout은 앞에서 살펴본 것처럼 random하게 일부 내용을 학습에서 skip하는 것이다.
따라서 학습된 알고리즘의 성능을 파악하는 test 과정에서 dropout을 적용하게 된다면, 매번 random한 결과가 발생할 것이다.
4. Understanding Dropout
Why does drop-out work?
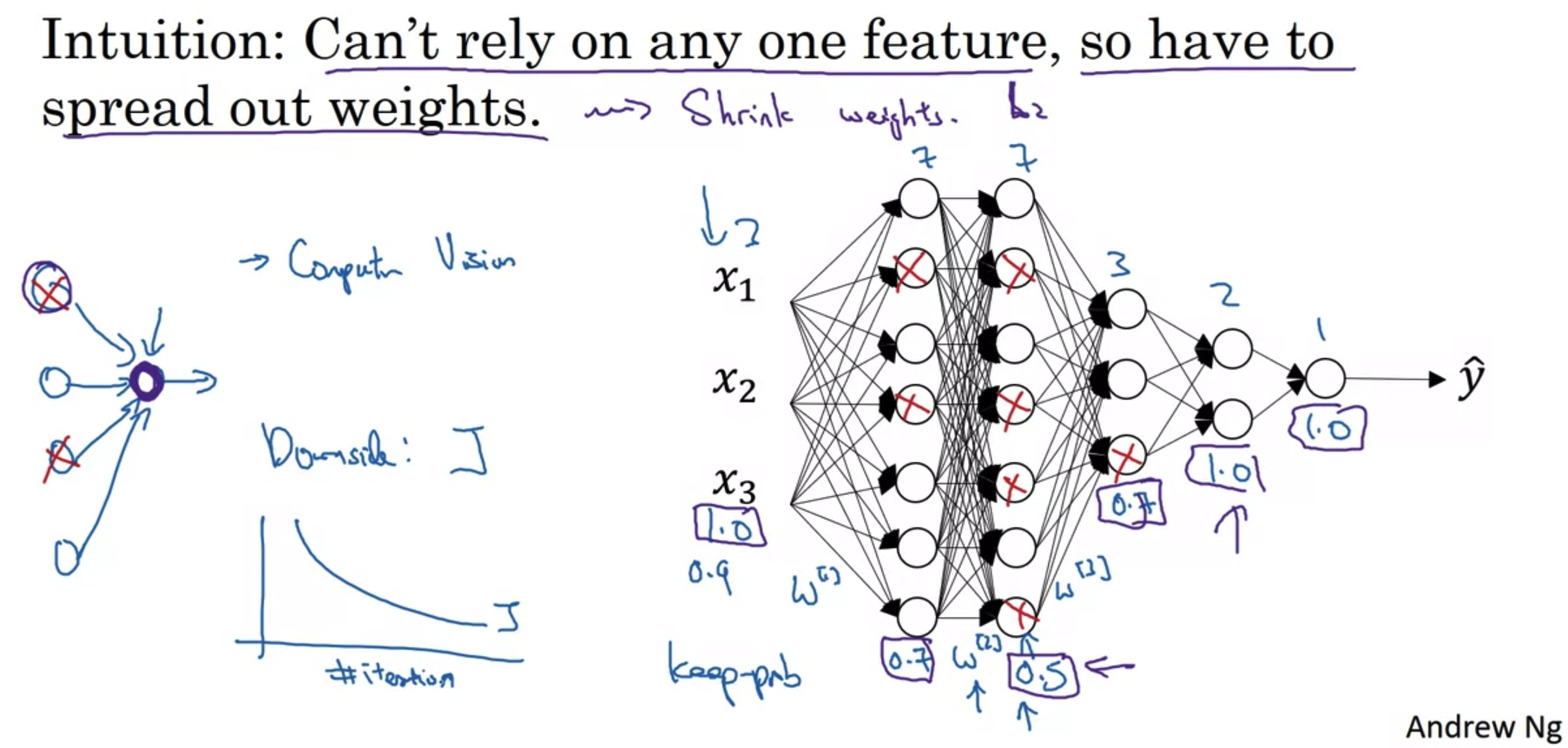
- dropout은 앞서 살펴보았던 L2 norm regularization(Frobenius norm) 방식과 굉장히 유사한 것으로 이해할 수 있다.
약간의 차이점이라면 Frobenius norm 방식은 사실 값을 0으로 만드는 것이 아니라 0에 근사하게 만드는 것이라는 점이다. - 그림의 오른쪽에 제시된 architecture를 살펴보자.
각 layer가 지닌 neruon 수가 다르기 때문에, 만약 over-fitting이 발생했다 하더라도 그 원인이 가중치 변수가 가장 많은 layer에 있을 가능성이 높다.
위 그림에서는 current layer, previous layer의 node수가 가장 많은 w2에서 over-fitting이 일어났을 가능성이 높다.
따라서 각 layer가 포함하는 가중치의 shape에 따라 다른 dropout 비율을 설정하는 것이 의미 있는 technique일 수 있다. - dropout은 over-fitting을 방지하는 훌륭한 regularization 기법이지만 단점도 존재한다.
back-propagation 과정에서 값의 업데이트가 일관성있는 패턴을 지니지 못하게 된다는 점이 그렇다.
따라서 교수님의 경우 dropout을 적용하지 않고 모델을 돌려보고 반복에 따라 cost function J가 줄어드는지 먼저 확인하신다고 한다.
dropout을 적용하지 않았을 때의 학습 과정이 정상적이라면, dropout을 적용하고 난 후 발생하는 문제점을 debugging하기 쉽기 때문이라고 설명하셨다.
5. Other Regularization Methods
Data augmentation
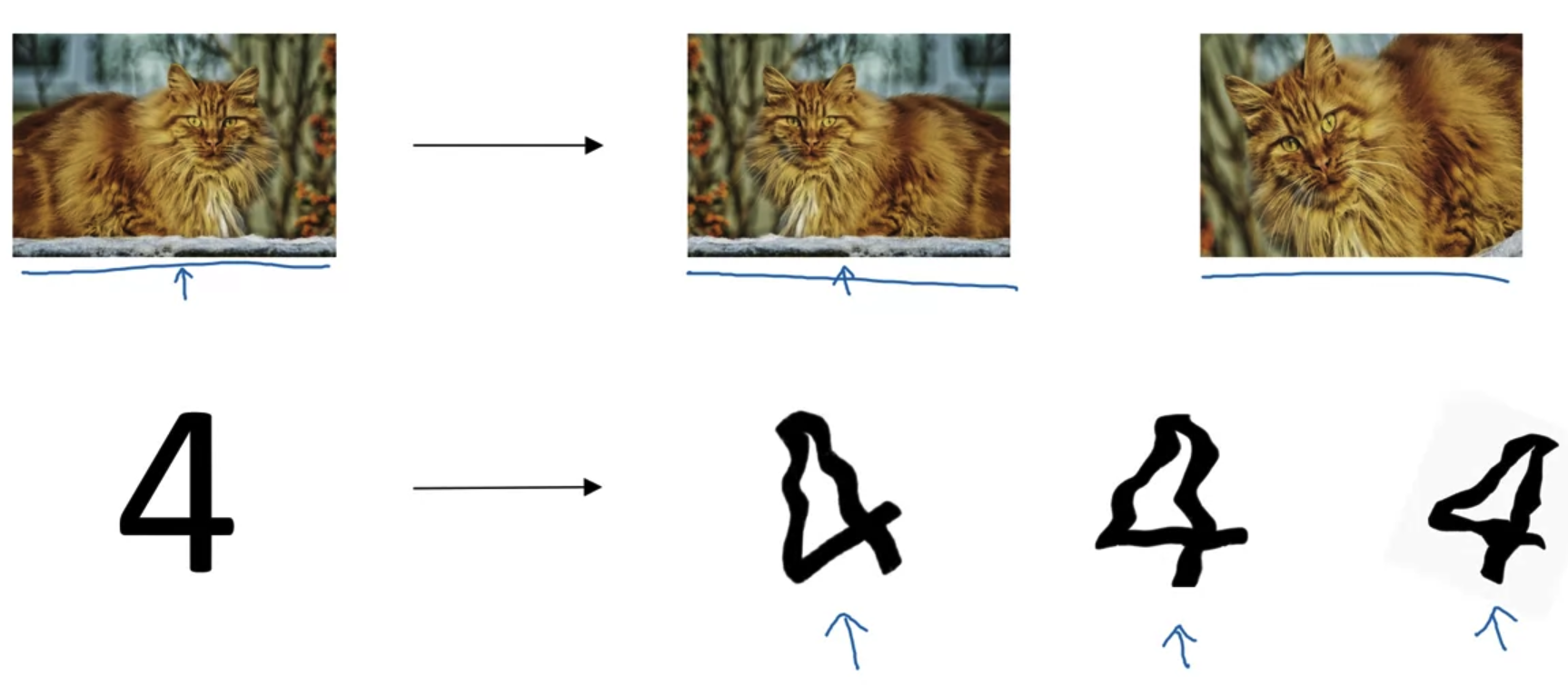
- 부족한 데이터의 양을 늘리기 위해 여러 방식을 적용할 수 있다.
특히 Computer Vision 분야의 경우 위와 같이 '뒤집기, 왜곡, 확대' 등의 변형을 통해 추가적인 비용 없이 데이터를 추가 확보 할 수 있다.
Early stopping
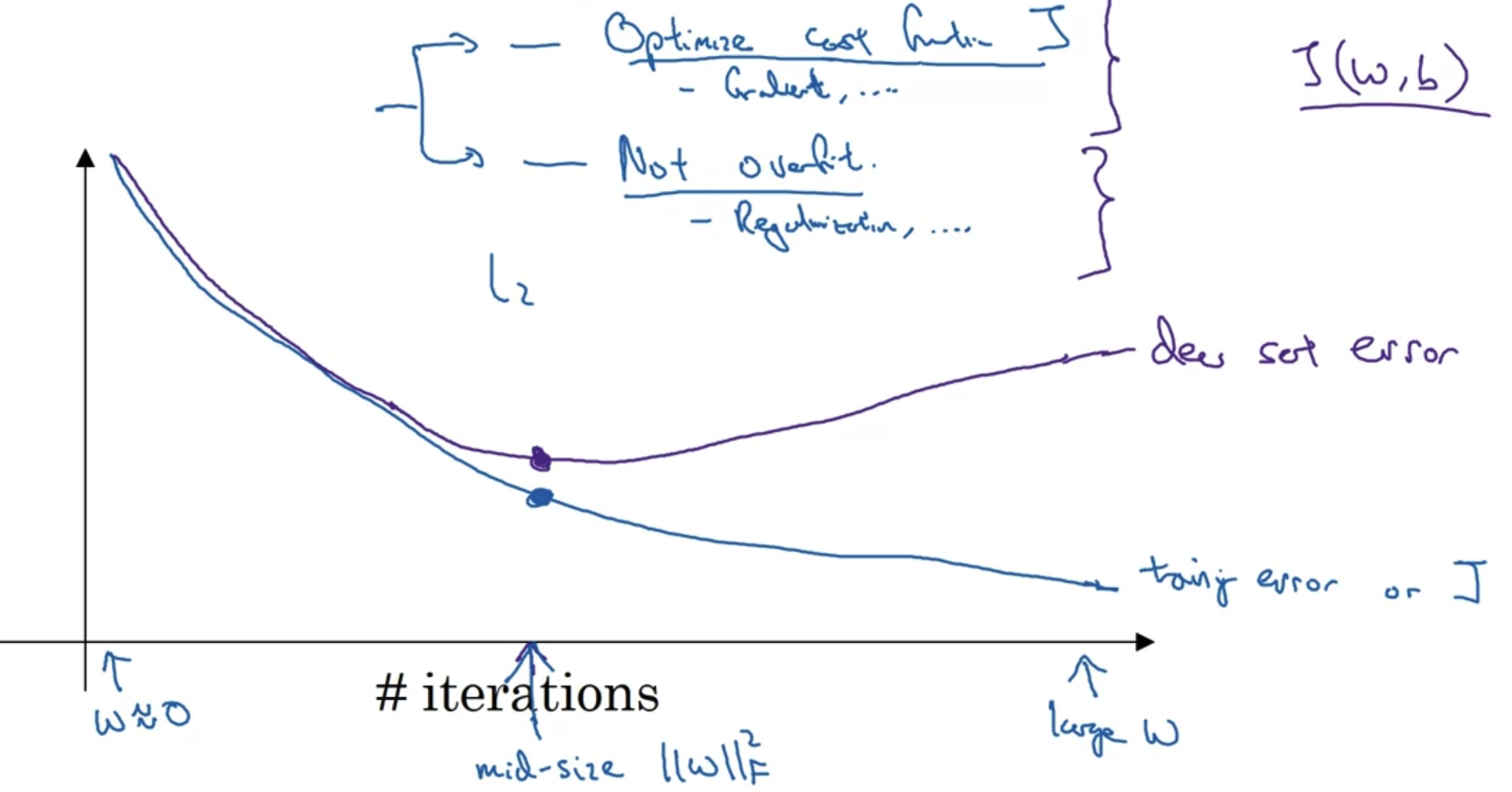
- Regularization의 또다른 방법으로 Early stopping이 있다.
위 그래프를 보면 반복 횟수가 많아질수록 train error는 감소하지만 dev error는 증가하면서 오히려 중간보다 모델의 성능이 떨어진다는 것을 알 수 있다.
이럴 경우에는 학습을 여러 번 반복하는 것보다는 중간에 멈춰서 그 결과를 이용하는 것이 더 좋을 것이다. - 그러나 이 방식도 단점이 없는 것은 아니다.
early stopping을 적용한다는 것은 결국 cost function을 최적화하는 과정을 중간에 멈추겠다는 뜻이 된다.
동시에 over-fitting을 방지하는 과정들도 중단되는 결과를 초래한다. - 그렇기 때문에 early stopping을 적용하지 않고 L2 norm regularization을 사용하면서 적절한 hyper parameter를 찾는 것도 방법이 될 수 있다.
하지만 early stopping을 적용하지 않으면 매번 다른 hyper parameter를 적용하면서 결과를 확인해야 하는 번거로움(일종의 비용)이 수반된다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 1주차' 카테고리의 다른 글
| Quiz & Assignments (0) | 2022.11.06 |
|---|---|
| Setting Up your Optimization(2) (0) | 2022.11.05 |
| Setting Up your Optimization Problem (0) | 2022.11.05 |
| Setting up your Machine Learning Application (0) | 2022.11.05 |
1. Regularization
Logistic regression
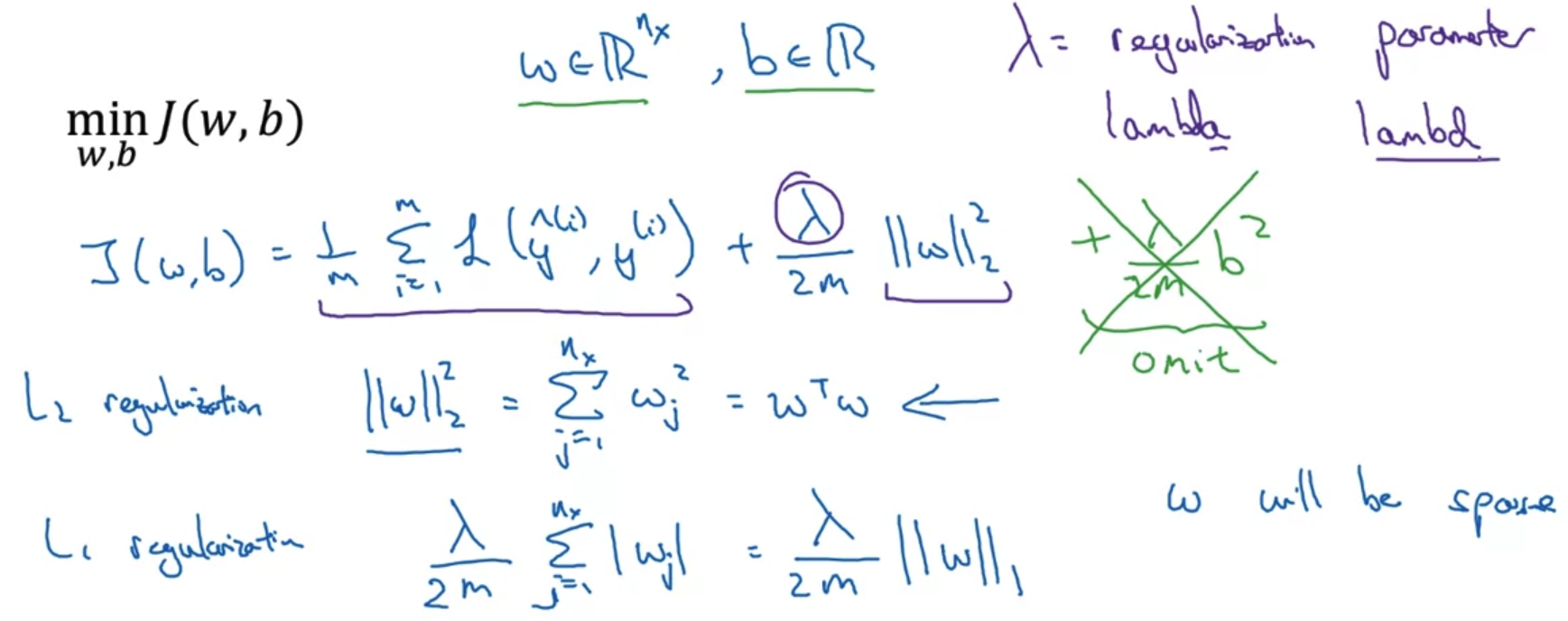
- High variance 문제가 있을 때 데이터를 늘리기 어려운 상황이라면 regularization을 적용할 수 있다.
loss function으로 구한 cost function J를 최소화하는 logistic regression을 예시로 들어 내용을 살펴보자. - 기존의 logistic regression에서는 J가 prediction과 target 간의 차이를 평균낸 것으로 정의된다.
여기에 lambda라는 일종의 hyper parameter와 전체의 개수 m으로 나눠준 값을 계수로 갖는 L2 norm을 곱한 값을 더해준다.
쉽게 말하면 '특정 계수와 L2 norm을 곱한 값의 평균'을 더해준다는 것이다. - 이때 두 변수 w와 b에 대해 모두 regularization을 적용할 필요는 없다.
왜냐하면 훨씬 더 많은 변수들을 포함하는 w와 달리 b는 하나의 값이므로 실제 over-fitting은 대부분 w의 변수들로 인해 발생하기 때문이다.
물론 원한다면 b에 대해서도 regularization을 적용할 수 있겠지만 큰 의미가 없을 가능성이 높다. - 뿐만 아니라 L1 regularization 방식도 존재한다.
이는 유클리언 방식으로 접근하는 L2와 달리 단순히 절댓값만을 구하는 방식으로,
이를 적용했을 때는 w가 이전에 비해 sparse한 형태를 띄게 만든다.
Neural network
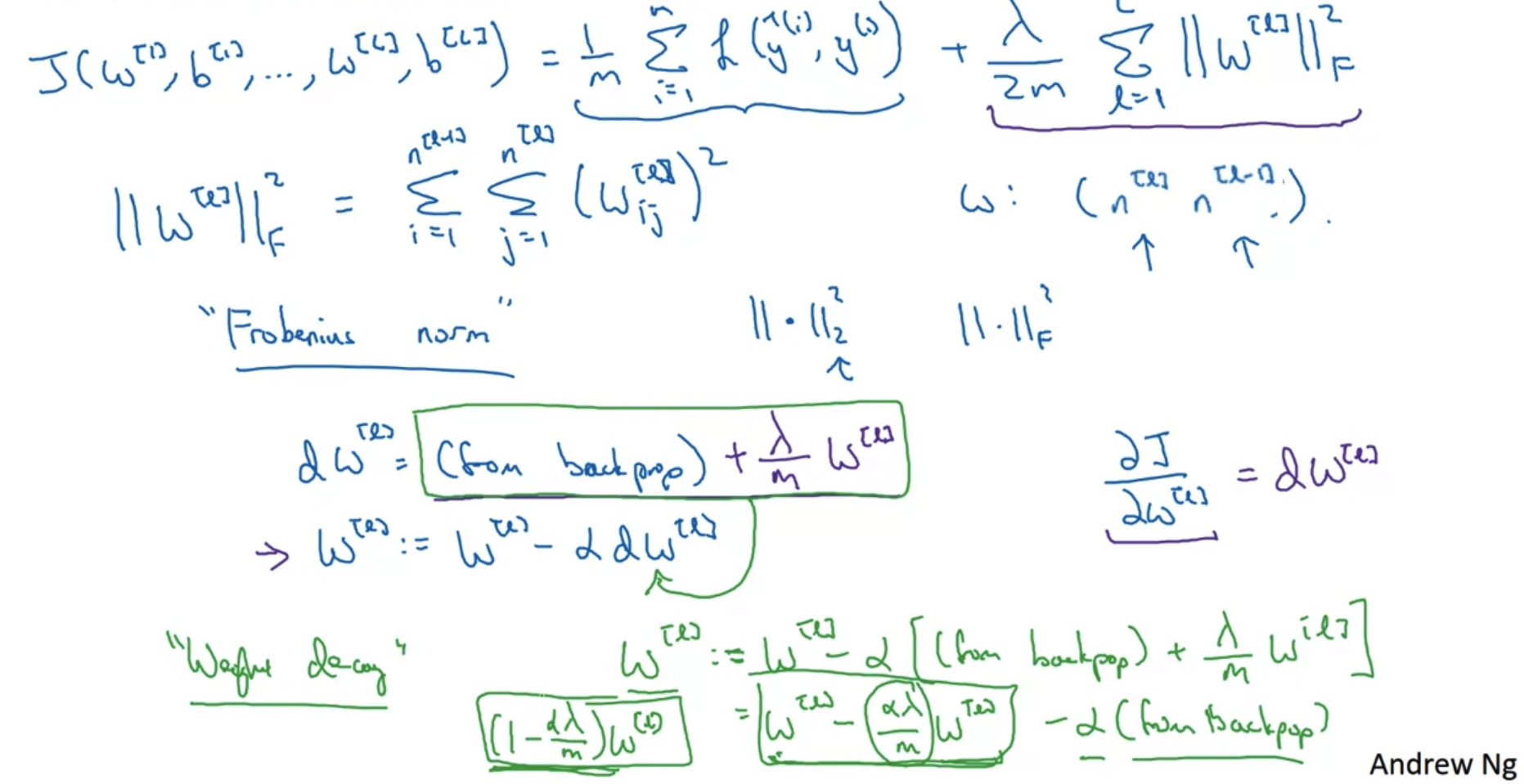
- Logistic regression의 문제를 neural network 문제로 확장시키면 어떻게 될까?
- 개념 자체는 동일하고 matrix로 확장된다는 점에만 유의하면 될 것이다.
- 이때 L2 norm으로 정의되는 부분을 여기서는 Frobenius norm이라고 부른다.
- Back-propagation에 의해 update되는 W를 자세히 살펴보자.
- 기존의 dw가 back-propagation에 의해 구해지는 결과였다면 여기에 Frobenius norm을 w에 대해 미분한 결과를 더해주어야 한다.
- w는 미분값을 alpha와 곱하여 빼줌으로써 업데이트 되는데 빼야하는 값이 커진다고 이해할 수 있다.
- Weight decay
- w가 변형된 dw를 빼면서 나온 결과를 잘 보면 기존의 가중치 w가 이전보다 줄어들었다는 것을 확인할 수 있다.
- 따라서 이런 식으로 L2 norm을 사용하여 regularization을 수행하는 것을 'weight decay'라고 부른다.
Frobenius norm을 보면 두 개의 시그마가 중첩되어 있는데 이때 i,j 범위가 바뀌어 있다.
i는 current layer, j는 previous layer의 숫자를 의미하기 때문에 두 범위를 바꿔주어야 한다.
2. Why Regularization Reduces overfitting?
How does regularization prevent overfitting?

- 새롭게 정의된 Cost function J를 보자.
우리는 back-propagation 과정에서 w의 값을 dw를 빼면서 update해준다.
따라서 새로 정의된 J에 따르면 lambda가 커질수록, update에서 빼야하는 dw가 커지면서 w는 사실상 '0'이 될 것이다. - 그러면 그림의 왼쪽 위 도식처럼 neural network 내부의 끊어져 마치 logstic regression을 여러 layer를 거쳐 쌓은 것과 유사한 구조가 될 것이다.
결국 이것이 의미하는 바는 'w라는 가중치가 prediction에 미치는 영향이 대폭 줄어들었다'는 것이다. - 물론 실제로는 lambda의 값이 커지더라도 w가 0이 되는 것은 아니지만,
w의 값이 굉장히 작아짐으로 인해 over-fitting이 완화되는 효과를 볼 수 있다. - 직관적으로 이해해보자면 맨 우측의 high variance의 형태를 좌측의 high bias로 유도하여 중간의 'just right'의 형태로 만들고자 하는 것이다.

- 위 내용을 activation function 관점에서도 해석해 볼 수 있다.
- 만약 regularization의 parameter lambda의 값이 매우 커진다면 앞서 확인한 것처럼 w의 값이 줄어들 것이다.
그렇다면 가중치 w와 편향 b를 더해 구한 z의 값도 줄어들 것임을 알 수 있다.
정확히는 z 값의 범위(range)가 굉장히 작아진다. - z값을 tan h 함수의 변수로 이용하여 g라는 변수를 구한다는 점을 떠올려 보자.
z의 값이 굉장히 작아지게 된다면 tan h의 x축 범위가 굉장히 작다는 것을 의미한다.
따라서 그 y 값의 범위도 작아지는데, 결과적으로 linear한 형태로 결과물이 도출된다. - 이는 여러 층의 nerual network를 만들어 비선형 근사를 했던 것을 다소 linear하게 만들어 줌으로써 over-fitting을 완화하는 것으로 이해할 수 있게 된다.
- 추가로 새롭게 정의된 cost function으로 모델을 돌리며 반복한 것과 실제 cost의 값을 그래프로 표현해보면 regularization을 적용했을 때 cost가 monotonically 감소하는 것을 확인할 수 있을 것이다.
3. Dropout Regularization

- Dropout은 over-fitting을 방지하기 위한 기법이다.
- 각 layer에 대해서 일정 확률로 연결을 끊고 학습을 진행한다.
결과적으로 더 작은 size의 neural network를 갖게 된다.
Implementing dropout("Inverted dropout")

- Dropout을 적용하는 방법은 위와 같다.(교수님의 손코딩..!)
layer가 3개인 network를 예시로 들어보자. - keep.prob은 기존 node를 유지할 비율을 뜻한다.
즉 이를 0.8로 설정하면 80%는 그대로 유지하고 20%는 shut off 하겠다는 것을 의미한다.
이 비율을 기준으로 a3의 shape을 딴 d3을 구해준다. - 이제 0과 1로 구성된(80%는 1, 20%는 0) d3을 a3과 곱해준다.
이때는 element-wise 연산을 수행하는 것이다. - dropout을 통해 a3에 포함되는 노드의 20%를 날려주고 나면 a3의 남은 80% 노드를 keep_prob = 0.8로 나눠야 한다.
이는 기존의 데이터 양을 보존하기 위함인데 예를 통해 알아보도록 하자.
기존 a3 노드가 100개라고 가정하자.(각 노드는 크기가 1이라고 생각한다)
만약 kee_prob = 0.8로 설정하여 dropout을 적용하면 80개의 노드가 남고 20개는 사라진다.
즉, 80개의 노드는 기존의 값을 유지하고 나머지 20개는 0이 되는 것이다.
결과적으로 처음에는 100만큼의 데이터가 있었지만 dropout을 적용함으로써 80만큼의 데이터만 남게 된다.
forward를 수행하는 과정에 있어서 데이터의 크기가 줄어든다면 layer가 여러 개인 network의 경우 데이터의 크기가 0에 수렴할 것이다.
결국 어떤 것도 학습하지 않게 되는 문제가 발생한다.
이를 해결하기 위해 80만큼의 남은 데이터를 0.8로 다시 나눠준다.
그러면 80 / 0.8 = 100 이므로 기존의 데이터 크기를 유지할 수 있게 된다.
즉, 기존의 데이터 크기를 유지하기 위해 dropout이 적용되는 각 layer마다 유지 비율(1-dropout 비율)로 나눠줌으로써 데이터의 크기를 보존하는 것이다.
Making predictions at test time
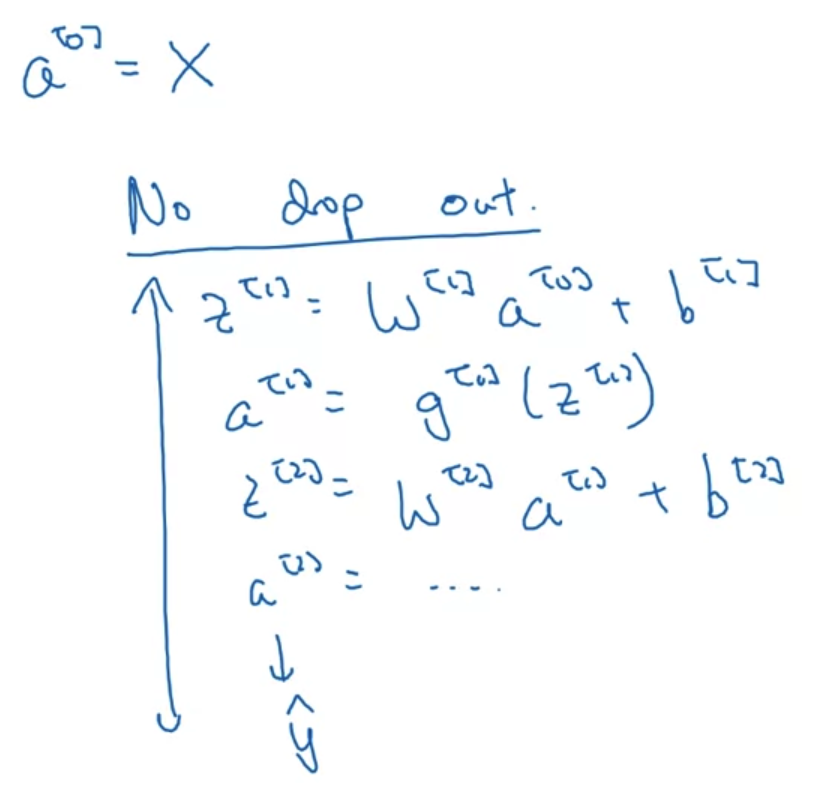
- test 할 때는 dropout을 적용하지 않는다.
- dropout은 앞에서 살펴본 것처럼 random하게 일부 내용을 학습에서 skip하는 것이다.
따라서 학습된 알고리즘의 성능을 파악하는 test 과정에서 dropout을 적용하게 된다면, 매번 random한 결과가 발생할 것이다.
4. Understanding Dropout
Why does drop-out work?

- dropout은 앞서 살펴보았던 L2 norm regularization(Frobenius norm) 방식과 굉장히 유사한 것으로 이해할 수 있다.
약간의 차이점이라면 Frobenius norm 방식은 사실 값을 0으로 만드는 것이 아니라 0에 근사하게 만드는 것이라는 점이다. - 그림의 오른쪽에 제시된 architecture를 살펴보자.
각 layer가 지닌 neruon 수가 다르기 때문에, 만약 over-fitting이 발생했다 하더라도 그 원인이 가중치 변수가 가장 많은 layer에 있을 가능성이 높다.
위 그림에서는 current layer, previous layer의 node수가 가장 많은 w2에서 over-fitting이 일어났을 가능성이 높다.
따라서 각 layer가 포함하는 가중치의 shape에 따라 다른 dropout 비율을 설정하는 것이 의미 있는 technique일 수 있다. - dropout은 over-fitting을 방지하는 훌륭한 regularization 기법이지만 단점도 존재한다.
back-propagation 과정에서 값의 업데이트가 일관성있는 패턴을 지니지 못하게 된다는 점이 그렇다.
따라서 교수님의 경우 dropout을 적용하지 않고 모델을 돌려보고 반복에 따라 cost function J가 줄어드는지 먼저 확인하신다고 한다.
dropout을 적용하지 않았을 때의 학습 과정이 정상적이라면, dropout을 적용하고 난 후 발생하는 문제점을 debugging하기 쉽기 때문이라고 설명하셨다.
5. Other Regularization Methods
Data augmentation

- 부족한 데이터의 양을 늘리기 위해 여러 방식을 적용할 수 있다.
특히 Computer Vision 분야의 경우 위와 같이 '뒤집기, 왜곡, 확대' 등의 변형을 통해 추가적인 비용 없이 데이터를 추가 확보 할 수 있다.
Early stopping

- Regularization의 또다른 방법으로 Early stopping이 있다.
위 그래프를 보면 반복 횟수가 많아질수록 train error는 감소하지만 dev error는 증가하면서 오히려 중간보다 모델의 성능이 떨어진다는 것을 알 수 있다.
이럴 경우에는 학습을 여러 번 반복하는 것보다는 중간에 멈춰서 그 결과를 이용하는 것이 더 좋을 것이다. - 그러나 이 방식도 단점이 없는 것은 아니다.
early stopping을 적용한다는 것은 결국 cost function을 최적화하는 과정을 중간에 멈추겠다는 뜻이 된다.
동시에 over-fitting을 방지하는 과정들도 중단되는 결과를 초래한다. - 그렇기 때문에 early stopping을 적용하지 않고 L2 norm regularization을 사용하면서 적절한 hyper parameter를 찾는 것도 방법이 될 수 있다.
하지만 early stopping을 적용하지 않으면 매번 다른 hyper parameter를 적용하면서 결과를 확인해야 하는 번거로움(일종의 비용)이 수반된다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 1주차' 카테고리의 다른 글
| Quiz & Assignments (0) | 2022.11.06 |
|---|---|
| Setting Up your Optimization(2) (0) | 2022.11.05 |
| Setting Up your Optimization Problem (0) | 2022.11.05 |
| Setting up your Machine Learning Application (0) | 2022.11.05 |