1. Practical aspects of Deep Learning (Quiz)
- examples의 수에 따라 train/dev/test set을 어떤 비율로 split 해야 하는가?
- 10,000개 정도로 작을 경우 : 60/20/20
- 20,000,000개 정도로 많을 경우 : 99/0.5/0.5
- training, test set은 같은 source로부터 구해진 것을 사용해야 한다.
그렇지 않을 경우 학습이 제대로 이루어지지 않는다. - 'high bias' 문제가 있는 경우 hidden layer 숫자를 늘려(deeper network) 해결을 시도할 수 있다.
'high variance' 문제의 경우 더 많은 train data를 확보하거나 regularization을 시도할 수 있다.- Data augmentation, L2 regularization, Dropout, ...
- training set error는 작고 dev set error는 큰 경우가 over-fitting이 발생한 것으로 'high variance' 문제에 해당한다.
regularization을 적용한다면 그 hyperparameter인 lambda의 값을 키워 high variance 문제를 해결할 수 있다. - regularization 기법으로는 dropout과 weight decay가 있다.
- dropout은 (1-keep_prob)의 확률로 unit을 제거하는 기법으로 overfitting을 방지한다.
- 만약 keep_prob을 0.5에서 0.6으로 증가시킨다면(drop rate을 감소시키면) regularization 효과는 줄어들고 training set error는 감소하는 결과가 나타날 것이다.
- input을 normalize하면 cost function이 더 빠른 속도로 optimize하게 된다.
2. Initialization (Programming Assignment)
weights의 초깃값을 어떻게 설정하는지에 따라 모델의 학습 성능이 달라지게 된다.
잘 설정한 초깃값은 다음과 같은 장점이 있다.
- gradient descent가 수렴하는 속도가 빨라진다.
- training error가 낮은 값으로 수렴할 가능성이 높아진다.
1) 두 parameter W,b 를 np.zeros를 이용하여 0으로 초기화한 경우

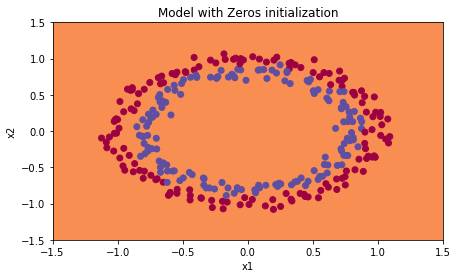
- weight와 bias가 모두 0이기 때문에 모든 vector가 0으로 채워진다.
결국 Wx + b를 통해 구해지는 z도 0이 되며, 이를 활성화 함수 ReLU에 집어 넣어도 0이 된다.
classification layer에서 sigmoid에 0을 대입하면 1/2이 나온다.
즉, 모든 예측 결과들이 전부 1/2 값을 갖고 loss function에 대입되는 것이다. - 이어서 prediction과 target을 비교하는 Loss function을 생각해보자.
logistic regression에서 사용했던 기존 공식에 따라 y=0이든 y=1이든지 간에 prediction이 0.5라면 그 결과는 무조건 동일하다.
즉, 값이 업데이트되지 않고 그대로 유지된다는 것이다. - np.zeors(tuple) 를 이용하여 0으로 초기화할 수 있다.
요약하면, weight & bias를 0으로 초기화하는 경우 학습이 전혀 진행되지 않는다.
따라서 여러 layer로 neural network를 구성했다 하더라도 logistic regression과 같은 linear classifier와 다를 바가 없어진다.
→ weight W는 반드시 random하게 초기화되어야 한다. bias b는 0으로 초기화되어도 괜찮다.
2) W를 np.random.randn을 이용하여 random하게 초기화한 경우(b는 0으로 초기화)
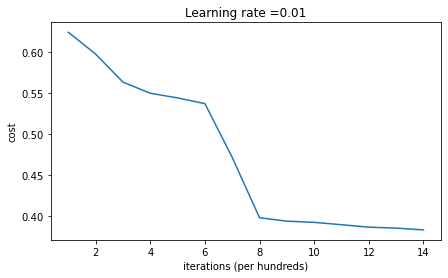

- W는 np.random.randn(x,y) * 10 으로 초기화하고 b는 np.zeros((tuple))로 초기화한다.
- np.random.rand( )은 uniform distribution으로 값을 생성한다.
np.random.randn( )은 normal distributino으로 값을 생성한다. - weight와 bias를 둘 다 0으로 초기화했을 때와 달리 iteration이 증가함에 따라 cost가 감소하는 것을 볼 수 있다.
지나치게 큰 값으로 weight를 초기화하는 것은 바람직하지 않다.
→ 어느 정도로 작은 값으로 초기화하는 것이 이상적일까?
3) He Initialization

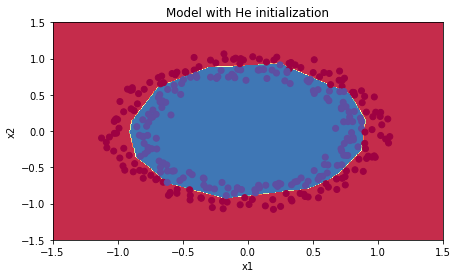
- Xavier Initialization과 굉장히 유사하다.
단, weight W를 sqrt(1./laeyrs_dims[l-1])로 나누는 것이 아니라 sqrt(2./layers_dims[l-1])로 나눈다는 차이점이 있다.
(sqrt는 제곱근을 뜻한다. np.sqrt( ) 형태로 사용 가능하다) - large random initialization과 비교했을 때 적은 iteration(반복)으로도 cost가 상당히 빠르게 줄어든다는 것을 확인할 수 있다.
Conclusion (Initialization)
- 다른 방식의 initialization은 다른 결과로 이어진다.
- Random initialization은 symmetry를 break하고 다른 hidden unit들이 다른 내용을 학습할 수 있도록 한다.
- 너무 큰 값으로 initialize하는 것을 지양해야 한다.
- 'He initialization'은 ReLU activation과 함께 사용할 때 효과가 좋다.
| Model | Train accruacy | Problem/Comment |
| 3-layer NN with zeros initialization | 50% | fails to break symmetry |
| 3-layer NN with large random initialization | 83% | too large weights |
| 3-layer NN with He initialization | 99% | recommended method |
3. Regularization (Programming Assignment)
Deep learning model이 over-fitting 하는 것을 방지하기 위해 regularization을 적용할 수 있다.
과제를 통해 regularization을 적용하지 않았을 때와 적용했을 때를 비교해보자.
Regularization
1) Non-Regularized
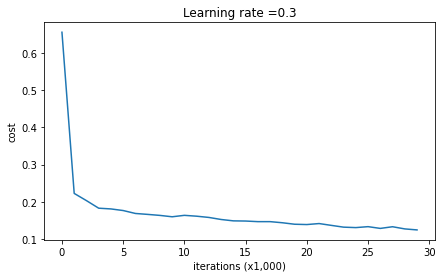
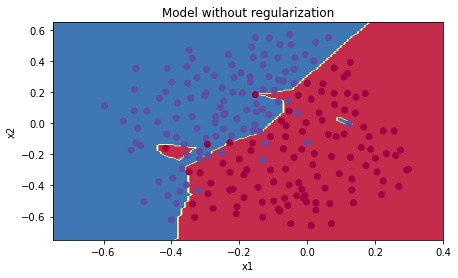
- 과제 상의 출력 결과를 보면 training set에 대한 정확도는 약 95%에 달하는 반면 test set에 대한 정확도는 92%에 채 미치지 못한다.
즉, over-fitting이 발생 것으로 볼 수 있다.
non-regularized model에서는 training set에 대해 over-fitting이 발생했다.
2) L2 Regularization
- cost with regularization
- 우선 cross_entropy_cost와 L2_regularization cost를 더해준다.
- 이때 np.sum(np.square( )) 함수를 사용하라고 문제에서 알려준다.
cross_entropy_cost = compute_cost(A3, Y)
L2_regularization_cost = (1/m) * (lambd/2) * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
cost = cross_entropy_cost + L2_regularization_cost- back-propagation with regularization
- forward에서 적용한 regularization을 미분하면 dJ/dW에 추가로 값이 붙는다.
- 이 내용 또한 공식으로 설명이 적혀 있으니 그대로 구현하면 된다.
dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * W3
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
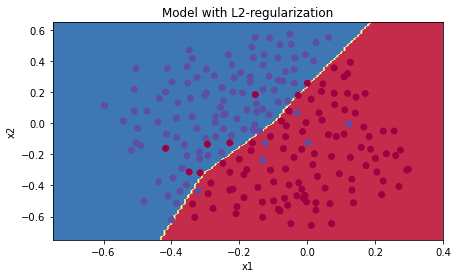
- regularization을 적용하고 모델을 돌리면 trainset과 test set의 정확도가 각각 93.8, 93으로 나온다.
즉, regularization을 적용하지 않았을 때보다 두 정확도 간의 차이가 줄어들었음을 알 수 있다.
1. cost function에 regularization term을 추가한다.
2. back-propagation에 extra term을 weight gradient에 추가한다.
→ wieght가 작은 값으로 줄어든다. "weight decay"
Dropout
Dropout은 regularization 기법 중 하나로 매 반복(iteration)마다 일부 neuron을 사용하지 않는 기법이다.
즉, 매번 다른 neuron들을 이용하여 학습을 하므로 특정 neuron에 대해 덜 민감(less sensitive)해진다.
다른 말로는 특정 data에 robust(강건)해진다고도 해석할 수 있을 것 같다.
1) forward propagation with dropout
D1 = np.random.rand(A1.shape[0],A1.shape[1])
D1 = (D1 < keep_prob).astype(int)
A1 = A1 * D1
A1 = A1 / keep_prob- A1과 shape이 동일한 D1을 random하게 생성한다.
이때 random.rand를 사용하면 uniform distribution을 이룬다.
이 D1에서 keep_prob보다 작은 값을 갖는 원소들은 0으로, keep_prob 이상의 값을 갖는 원소들은 1로 바꿔준다. - A1을 D1과 곱해줌으로써 keep_prob의 비율에 맞게 A1의 원소들을 남긴다.
마지막으로 이를 keep_prob으로 나눠줌으로써 dropout을 적용하지 않았을 때와 동일한 크기의 value를 유지하도록 한다.
2) backward propagation with dropout
dA2 = dA2 * D2
dA2 = dA2 / keep_prob
dA1 = dA1 * D1
dA1 = dA1 / keep_prob- back-propagation에 dropout을 적용하는 것은 간단하다.
forward propagation에서 cache에 저장해둔 D1, D2를 그대로 사용하면 된다. - dropout을 적용하지 않았을 때의 dA1, dA2에 각각 D1, D2를 곱해준다.
그리고 forward에서와 마찬가지로 기존의 value 크기를 유지하기 위해 keep_prob로 나눠주면 된다.

- 이때 train/test set에 대한 accuracy를 확인해보면 각각 약 93, 95점이 기록되었음을 확인할 수 있다.
즉 dropout을 적용했을 경우 train set에 대해 over-fitting되지 않으면서도 inference 결과가 좋아진다는 것이다.
Keep in mind that
1. Dropout은 regularization 기법 중 하나다.
2. Dropout은 train 동안에만 적용해야 한다. test set에 대해 적용하면 안 된다.
3. Dropout은 forward / backward propagation에 둘 다 적용해야 한다.
4. Dropout을 적용할 때는 반드시 연산 결과를 keep_prob로 나눠줘야 한다.
이는 기존의 value 크기를 유지하기 위함이다.
Conclusions (Regularization)
- Regularization은 over-fitting 경향을 줄여준다.
- Regularization은 weights를 낮은 값으로 변경해준다.
- L2 regularization과 Dropout은 아주 효과적인 regularization 기법이다.
| Model | Train accruacy | Test accuracy |
| 3-layer NN without regularization | 95% | 91.5% |
| 3-layer NN with L2-regularization | 94% | 93% |
| 3-layer NN with dropout | 93% | 95% |
4. Gradient Checking (Programming Assignment)
Back-propagation은 gradient ∂𝐽/∂𝜃를 계산하는 것이다.
만약 계산이 정확하다면 J(θ+ε)와 J(θ−ε)를 구하여 미분의 정의에 따라 계산한 값과 동일한 결과가 도출될 것이다.
1-Dimensional Gradient Checking
1) forward propagation
J = theta * x- 이 예시에서는 cost function을 linear function인 J = θx 로 정의한다.
2) backward propagtion
dtheta = x- forward에서 정의한 cost function J를 θ에 대해 미분하면 x가 된다.
3) gradient check
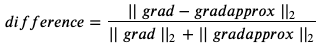
# 1. 근사 미분계수
theta_plus = theta + epsilon
theta_minus = theta - epsilon
J_plus = forward_propagation(x, theta_plus)
J_minus = forward_propagation(x, theta_minus)
gradapprox = (J_plus-J_minus) / (2*epsilon)
# 2. 미분계수 - 근사 미분계수 차이
numerator = np.linalg.norm(grad-gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator- 문제에서 주어진 식을 기반으로 코드를 작성하면 된다.
약간 주의할 점은 근사 미분계수가 아닌 기존의 미분계수를 구할 때는 grad로 정의하는데,
이는 이전에 정의한 backward_propagation 함수를 이용하여 값을 구해야 한다. - 근사 미분계수를 굉장히 작은 숫자 epsilon을 통해 구하고,
이를 기존 미분계수 grad와 계산하면 된다.
이때의 둘의 차를 L2 norm으로 계산한 것을 분자로, 각각의 L2 norm을 더한 것을 분모로 삼아 차이를 계산한다.
이 차이(difference)가 특정 수치를 넘는지 넘어가지 않는지 확인하는 것이 gradient check라고 볼 수 있다.
N-Dimensional Gradient Checking
layer가 추가되어 forward, backward propagation 과정이 조금 길어졌다는 점과 vector 형태로 계산이 된다는 점을 제외하면 이전과 동일한 process를 거치게 된다.
Gradient Checking 구현에 있어서 필수적인 코드들은 아래와 같다.
for i in range(num_parameters):
# theta + epsilon
theta_plus = np.copy(parameters_values)
theta_plus[i] = theta_plus[i] + epsilon
J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(theta_plus))
# theta - epsilon
theta_minus = np.copy(parameters_values)
theta_minus[i] = theta_minus[i] - epsilon
J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(theta_minus))
# 근사 미분계수 구하기(극한을 제외한 미분 정의)
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2*epsilon)
# difference 구하기 (분자/분모)
numerator = np.linalg.norm(grad-gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator- theta + , theta - 를 구하는 방식은 1-Dimensional에서와 동일하다.
단, 이때는 vector로 연산을 수행해야 하므로 gc_utils의 'dictionary_to_vector, vector_to_dictionary' 함수를 사용한다. - i 번째의 cost값을 구할 때는 이전에 정의한 forward_propagation_n 함수를 이용하도록 한다.
이때 parameter는 X, Y와 더불어 변형된 theta값을 인자로 받는 dict가 된다. - 우리가 구한 근사 미분계수와 실제 미분계수가 얼마만큼의 차이나는지 식을 통해 구한다.
이전과 마찬가지로 np.linalg.norm을 통해 제시된 공식을 코드로 구현하면 된다.
결과적으로 backward propagation에 문제가 있다는 것이 확인되어야 정답이다.
Conclusions
- Gradient Checking은 시간이 오래 걸리는 작업이다.
따라서 우리는 매 iteration마다 수행하는 것이 아니라 gradient가 정확한 값을 갖는지 몇 번 정도만 확인할 때 사용한다. - Gradient Checking은 Dropout 기법과 동시에 사용될 수 없다.
dropout이 random하게 적용되기 때문에 어디서 문제가 발생했는지 파악하기가 어렵기 때문이다.
따라서 dropout을 적용하지 않은 상태에서 gradient checking을 해야 한다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 1주차' 카테고리의 다른 글
| Setting Up your Optimization(2) (0) | 2022.11.05 |
|---|---|
| Setting Up your Optimization Problem (0) | 2022.11.05 |
| Regularizing your Neural Network (2) | 2022.11.05 |
| Setting up your Machine Learning Application (0) | 2022.11.05 |
