목차
4. Numerical Approximation of Gradients
Checking your derivative computation

- 미분의 정의를 통해 접선의 기울기를 계산하는 과정을 이해해보자.
- x = θ일 때 아주 작은 값 ε = 0.01을 더하고 빼서 함수값을 구해본다.
본래 기울기는 'y의 변화량 / x의 변화량' 이므로 {f(θ+ε) - f(θ-ε)} / 2ε 이 기울기가 된다.
이는 함수 f(θ) = θ^3을 미분하여 구한 g(θ) = 3θ^2와 근사한 결과다. - 실제 값을 대입해보면 미분값이 3.0001로 기존 도함수 g를 통해 구한 3과 0.0001 차이가 나는 것을 알 수 있다.
계산은 이와 같은 방식으로 이뤄진다.
이때의 error는 O(ε^2)로 표현된다. - 이를 기존 미분 정의와 비교해보면, 즉 x = θ 와 x = θ + ε 만을 통해 구한 미분계수와 비교해보면 error가 0.01로 커진다는 것을 확인할 수 있다.
이때의 error는 O(ε)로 표현된다.
5. Gradient Checking
Graident check for a neural network
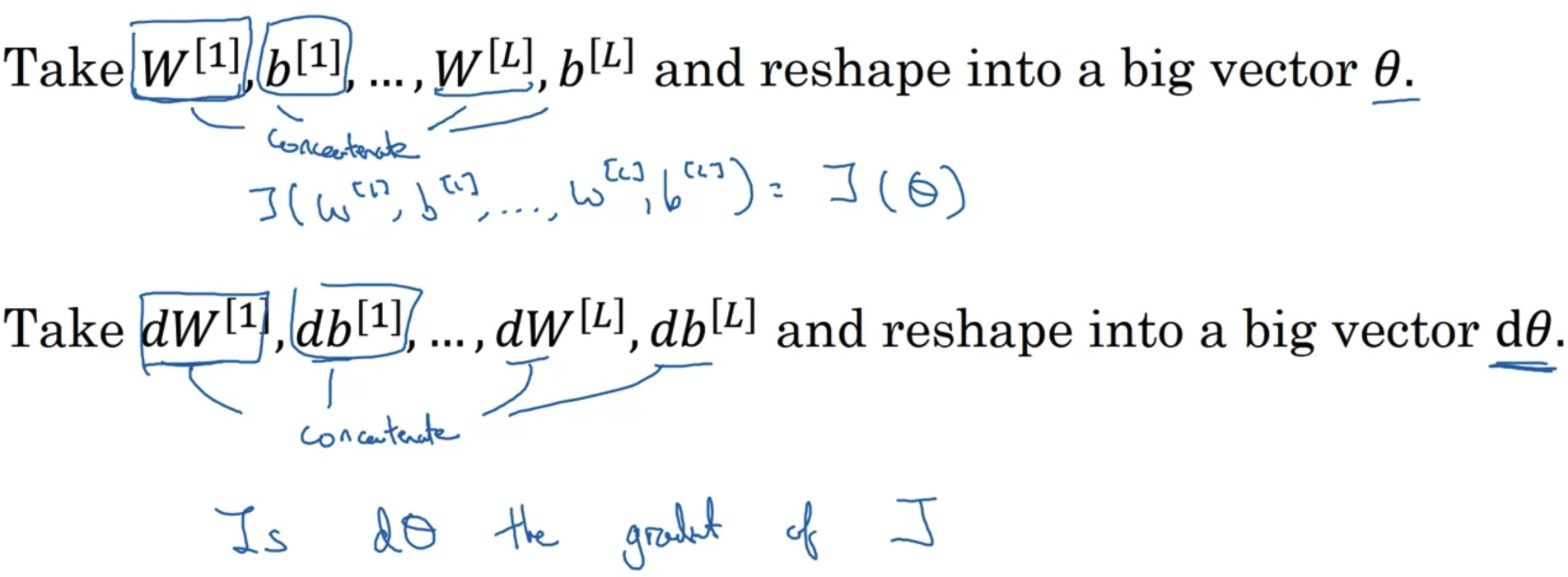
- forward에서 사용되는 변수 w,b를 모두 합쳐서(concat) matrix 형태로 변환한다.
마찬가지로 backward에서 사용되는 변수 dW,db를 모두 합쳐서(concat) matrix 형태로 변환한다. - 만약 forward의 matrix를 θ라고 한다면 dθ는 cost function J의 gradient일까?
Gradient checking (Grad check)
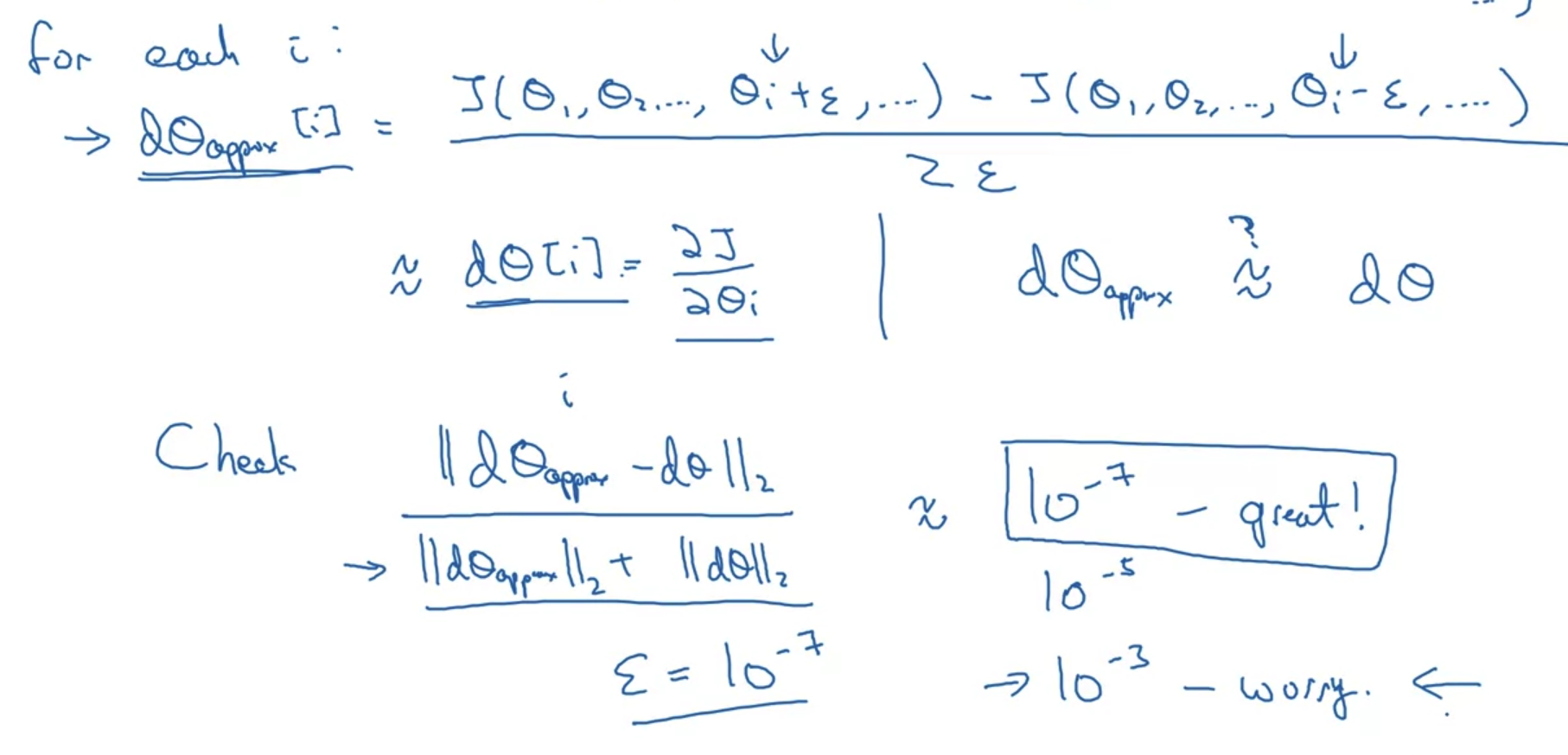
- dθ를 근사하여 구한 식을 통해 계산을 하면 오차가 어느 정도인지 확인하는 과정이다.
- graident check 식은 위 그림의 아래 부분을 확인하면 된다.
여기서는 L2 norm을 사용하여 유클리드 거리를 구한다.
그리고 이것을 각 근사의 길이 합으로 나눠준다. - 위 식을 통해 오차를 확인해보면 그 오차가 ε의 크기에 비례하는 것을 알 수 있다.
즉 ε = e-7인 경우 great, ε = e-5인 경우 normal, e = e-3인 경우 위험하다.
위험하다는 의미는 거의 대부분의 계산에 있어서 오차가 있는지 확인해야 한다는 뜻이다.
6. Gradient Checking Implementation Notes

- train 과정에서 debug를 위해 gradient check를 함께 수행하면 train 속도가 너무 느리기 때문에 train 중에는 gradient checking을 지양한다.
- 근사한 미분계수에 error가 있는 것이 확인되면 몇 번째 layer에서 발생한 것인지 따로 확인을 해봐야 한다.
- gradient check를 할 때는 regularization을 적용했는지 확인해야 한다.
- dropout이 적용되면 어떤 부분에서 문제가 발생했는지 파악하는 것이 어렵다.
dropout은 일정 비율에 따라 random하게 적용되기 때문이다.
따라서 dropout을 적용하지 않고 gradient check를 통해 해당 algorithm이 정상적으로 작동하는지 먼저 확인하고 dropout을 적용하도록 하자. - 때때로 w,b가 0에 수렴하는 값을 가지면서 정상적으로 학습이 되지 않을 수 있다.
따라서 w,b가 0에 가까운 값에서 맴돌고 있지는 않은지 확인해볼 필요가 있다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 1주차' 카테고리의 다른 글
| Quiz & Assignments (0) | 2022.11.06 |
|---|---|
| Setting Up your Optimization Problem (0) | 2022.11.05 |
| Regularizing your Neural Network (2) | 2022.11.05 |
| Setting up your Machine Learning Application (0) | 2022.11.05 |
4. Numerical Approximation of Gradients
Checking your derivative computation

- 미분의 정의를 통해 접선의 기울기를 계산하는 과정을 이해해보자.
- x = θ일 때 아주 작은 값 ε = 0.01을 더하고 빼서 함수값을 구해본다.
본래 기울기는 'y의 변화량 / x의 변화량' 이므로 {f(θ+ε) - f(θ-ε)} / 2ε 이 기울기가 된다.
이는 함수 f(θ) = θ^3을 미분하여 구한 g(θ) = 3θ^2와 근사한 결과다. - 실제 값을 대입해보면 미분값이 3.0001로 기존 도함수 g를 통해 구한 3과 0.0001 차이가 나는 것을 알 수 있다.
계산은 이와 같은 방식으로 이뤄진다.
이때의 error는 O(ε^2)로 표현된다. - 이를 기존 미분 정의와 비교해보면, 즉 x = θ 와 x = θ + ε 만을 통해 구한 미분계수와 비교해보면 error가 0.01로 커진다는 것을 확인할 수 있다.
이때의 error는 O(ε)로 표현된다.
5. Gradient Checking
Graident check for a neural network
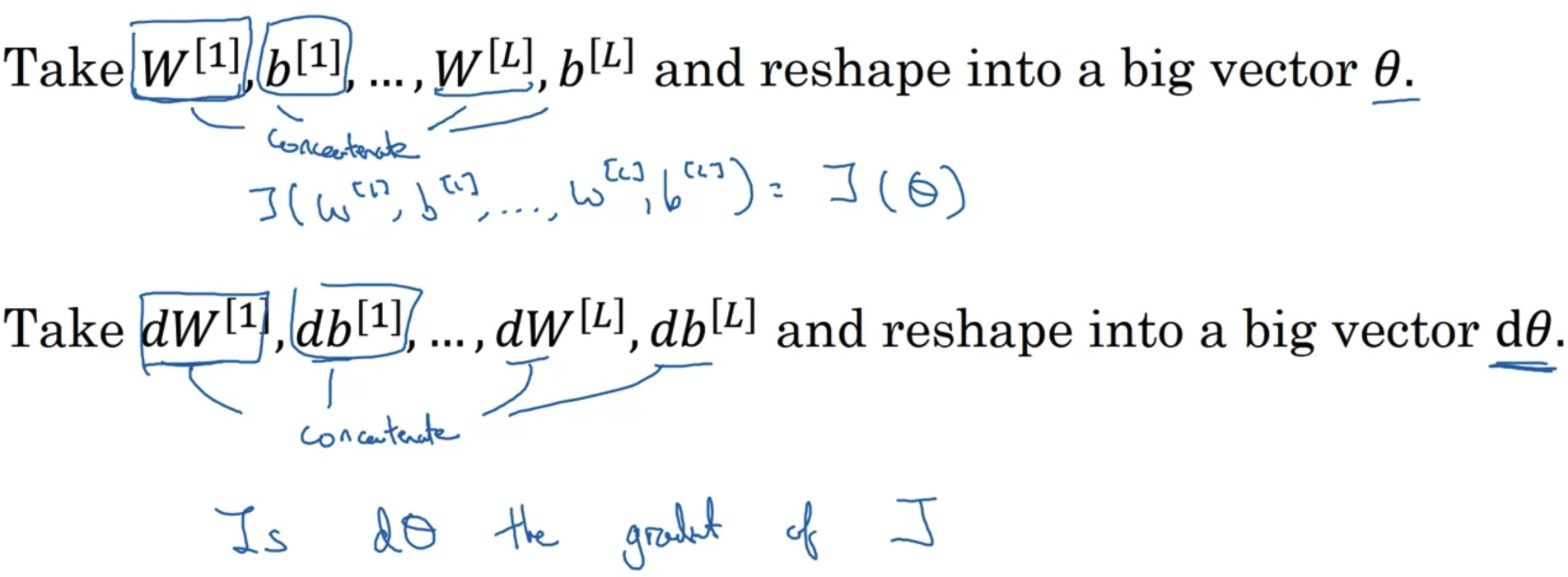
- forward에서 사용되는 변수 w,b를 모두 합쳐서(concat) matrix 형태로 변환한다.
마찬가지로 backward에서 사용되는 변수 dW,db를 모두 합쳐서(concat) matrix 형태로 변환한다. - 만약 forward의 matrix를 θ라고 한다면 dθ는 cost function J의 gradient일까?
Gradient checking (Grad check)
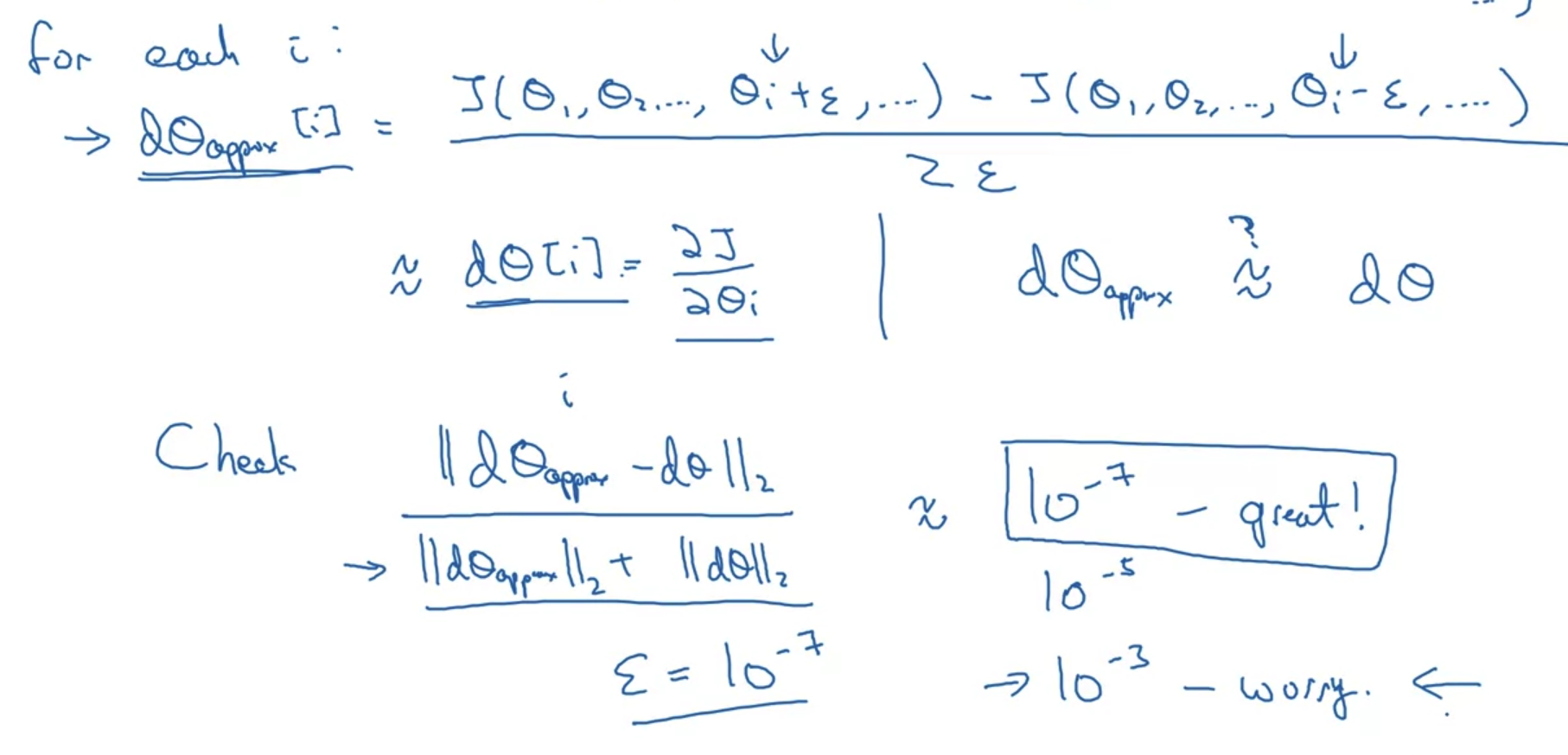
- dθ를 근사하여 구한 식을 통해 계산을 하면 오차가 어느 정도인지 확인하는 과정이다.
- graident check 식은 위 그림의 아래 부분을 확인하면 된다.
여기서는 L2 norm을 사용하여 유클리드 거리를 구한다.
그리고 이것을 각 근사의 길이 합으로 나눠준다. - 위 식을 통해 오차를 확인해보면 그 오차가 ε의 크기에 비례하는 것을 알 수 있다.
즉 ε = e-7인 경우 great, ε = e-5인 경우 normal, e = e-3인 경우 위험하다.
위험하다는 의미는 거의 대부분의 계산에 있어서 오차가 있는지 확인해야 한다는 뜻이다.
6. Gradient Checking Implementation Notes

- train 과정에서 debug를 위해 gradient check를 함께 수행하면 train 속도가 너무 느리기 때문에 train 중에는 gradient checking을 지양한다.
- 근사한 미분계수에 error가 있는 것이 확인되면 몇 번째 layer에서 발생한 것인지 따로 확인을 해봐야 한다.
- gradient check를 할 때는 regularization을 적용했는지 확인해야 한다.
- dropout이 적용되면 어떤 부분에서 문제가 발생했는지 파악하는 것이 어렵다.
dropout은 일정 비율에 따라 random하게 적용되기 때문이다.
따라서 dropout을 적용하지 않고 gradient check를 통해 해당 algorithm이 정상적으로 작동하는지 먼저 확인하고 dropout을 적용하도록 하자. - 때때로 w,b가 0에 수렴하는 값을 가지면서 정상적으로 학습이 되지 않을 수 있다.
따라서 w,b가 0에 가까운 값에서 맴돌고 있지는 않은지 확인해볼 필요가 있다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 1주차' 카테고리의 다른 글
| Quiz & Assignments (0) | 2022.11.06 |
|---|---|
| Setting Up your Optimization Problem (0) | 2022.11.05 |
| Regularizing your Neural Network (2) | 2022.11.05 |
| Setting up your Machine Learning Application (0) | 2022.11.05 |
