목차
1. Exponentially Weighted Averages (지수 가중 평균)
Temperature in London
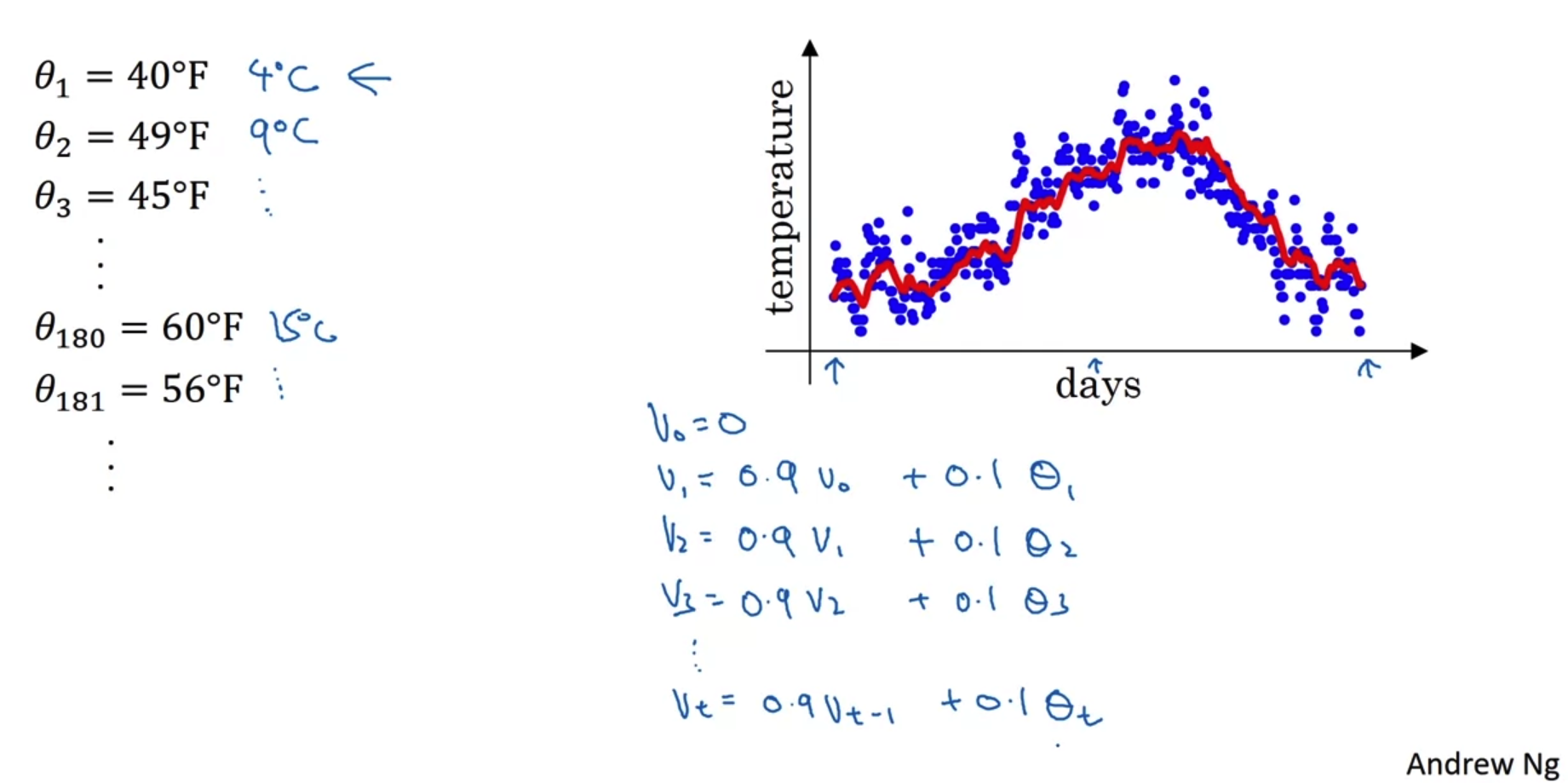
- 영국의 1년 날씨를 날짜에 따라 표시한 그래프다.
전날과 오늘의 관계를 수식적으로 표현하여 그래프가 그려지는 양상을 예측하고자 한다.
Exponentially weighted averages
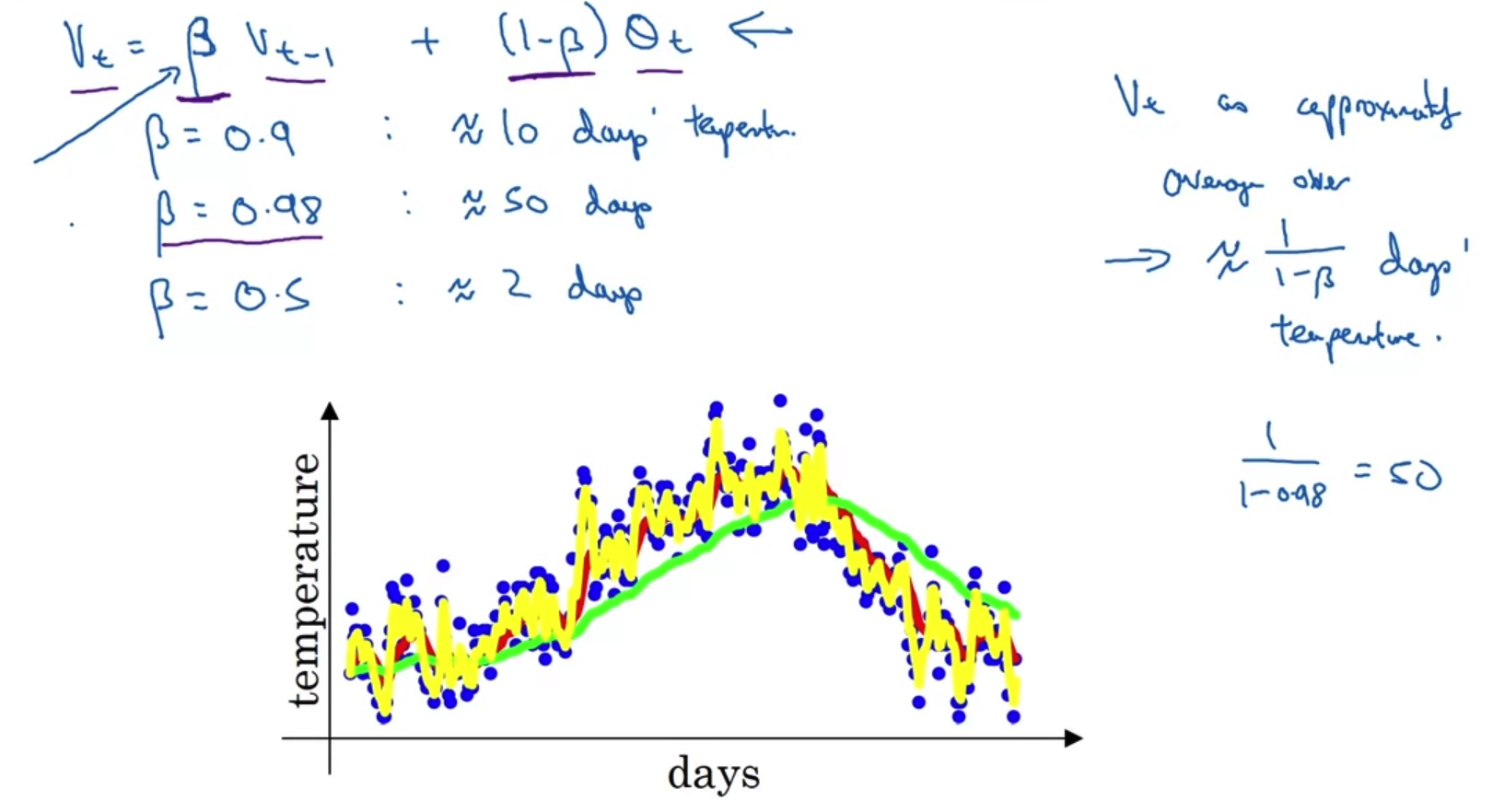
- V_t 로 표현된 수식이 Exponentially wieghted averages에 대한 수식이다.
이는 과거의 비중(가중치)을 베타로 표현하고 오늘의 비중을 세타로 표현하고 있다. - 따라서 베타가 아주 큰 경우에는 과거의 기록을 더 많이 반영하게 되므로 그래프가 완만한 초록색 선으로 표현된다.
대신 말 그대로 과거의 기록을 더 많이 반영하기 때문에 실제 데이터보다는 약간 우측에 치우치게 된다. - 반면 베타가 0.5인 경우에는 직전 하루만의 과거 정보를 다룬다는 의미가 된다.
즉 어제와 오늘의 정보를 반반 이용하겠다는 뜻이므로 아주 촘촘한 노란색 그래프로 표현된다.
이때는 변화에 굉장히 예민하다고 볼 수 있다.
2. Understanding Exponenetailly Weighted Averages
Exponentailly weighted averages

- 그림의 우측 상단 두 그래프를 먼저 살펴보자.
위의 그래프는 100일간의 기온을 x로 표시한 것이고, 아래의 그래프는 그 기온에 곱해지는 계수를 지수함수꼴로 표현한 것이다.
우리는 두 그래프의 각 값을 곱하여 100일간의 평균 기온을 구할 수 있다. - 베타가 0.9인 경우 100일간의 평균 기온을 구하는 전개식을 확인할 수 있다.
이때 계수가 지니는 의미를 살펴보면 1/e값이 되는 지점을 구하면 된다.
예를 들어 0.9의 10승은 약 0.35로 1/e값에 근사한다.
즉, 10일이 지나면 원래의 가중치보다 1/3만큼으로 줄어든 가중치를 적용하게 된다는 뜻이다. - 전개식의 의미를 다시 생각해보면 각 온도에 곱해지는 계수는 1 또는 1에 아주 근사한 값을 갖는다.
그렇기 때문에 이를 Exponentially weighted averages라고 부른다.
Implementing exponentially weigthed averages
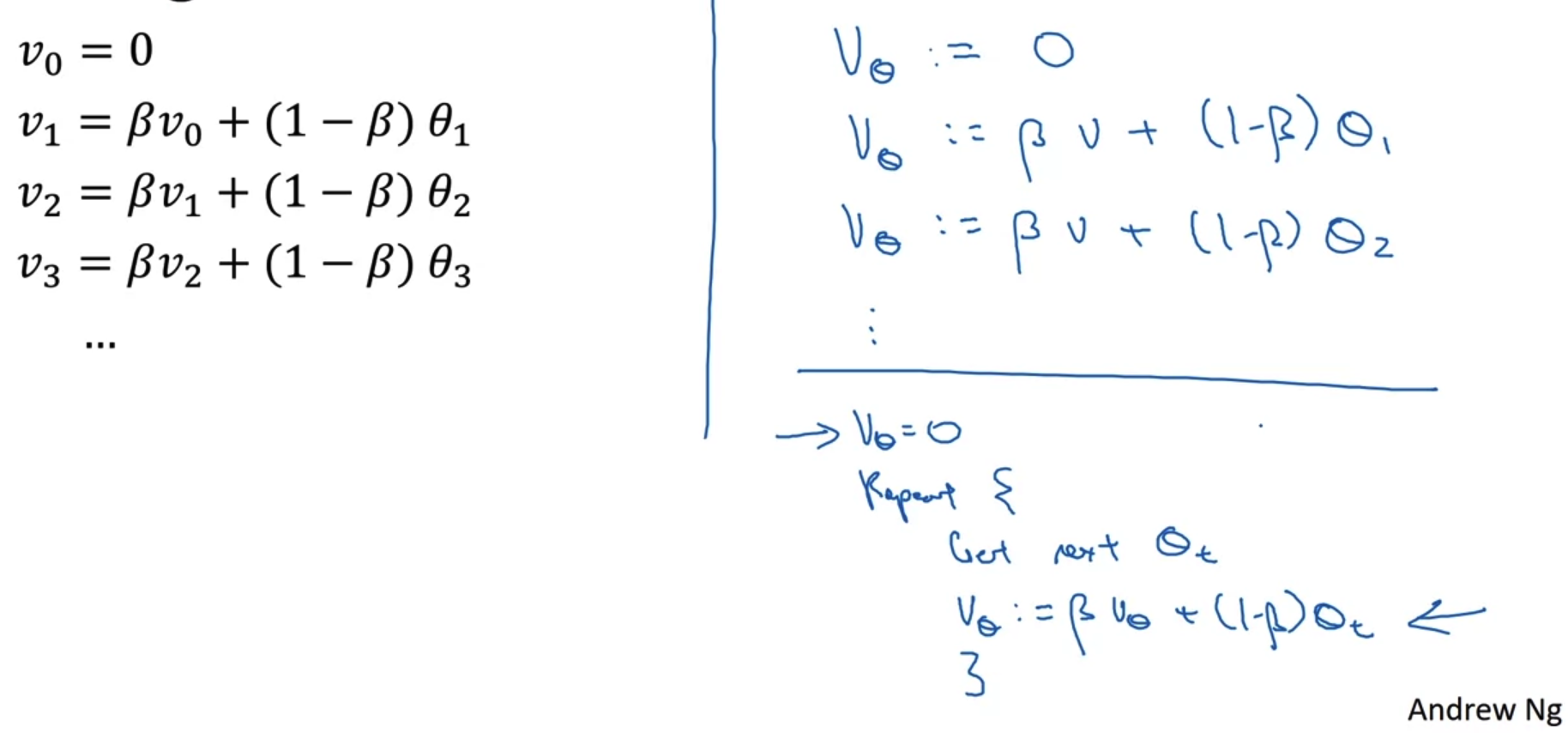
- exponentially weighted averages를 이용하는 방법은 위처럼 반복적인 식을 적용하는 것이다.
따라서 같은 식을 여러 번 반복해서 쓸 필요없이 반복문을 통해 간단히 계산할 수 있다. - 이런 방식은 모든 값들을 한꺼번에 메모리에 저장할 필요를 없어지게 함으로써 메모리 효율적이다.
그렇기 때문에 연산 속도도 매우 빠르다.
한 줄 짜리 코드로 표현할 수 있는만큼 구현하기 간편하다는 장점도 지닌다.
3. Bias Correction in Exponentially Weighted Averages
Bias correction
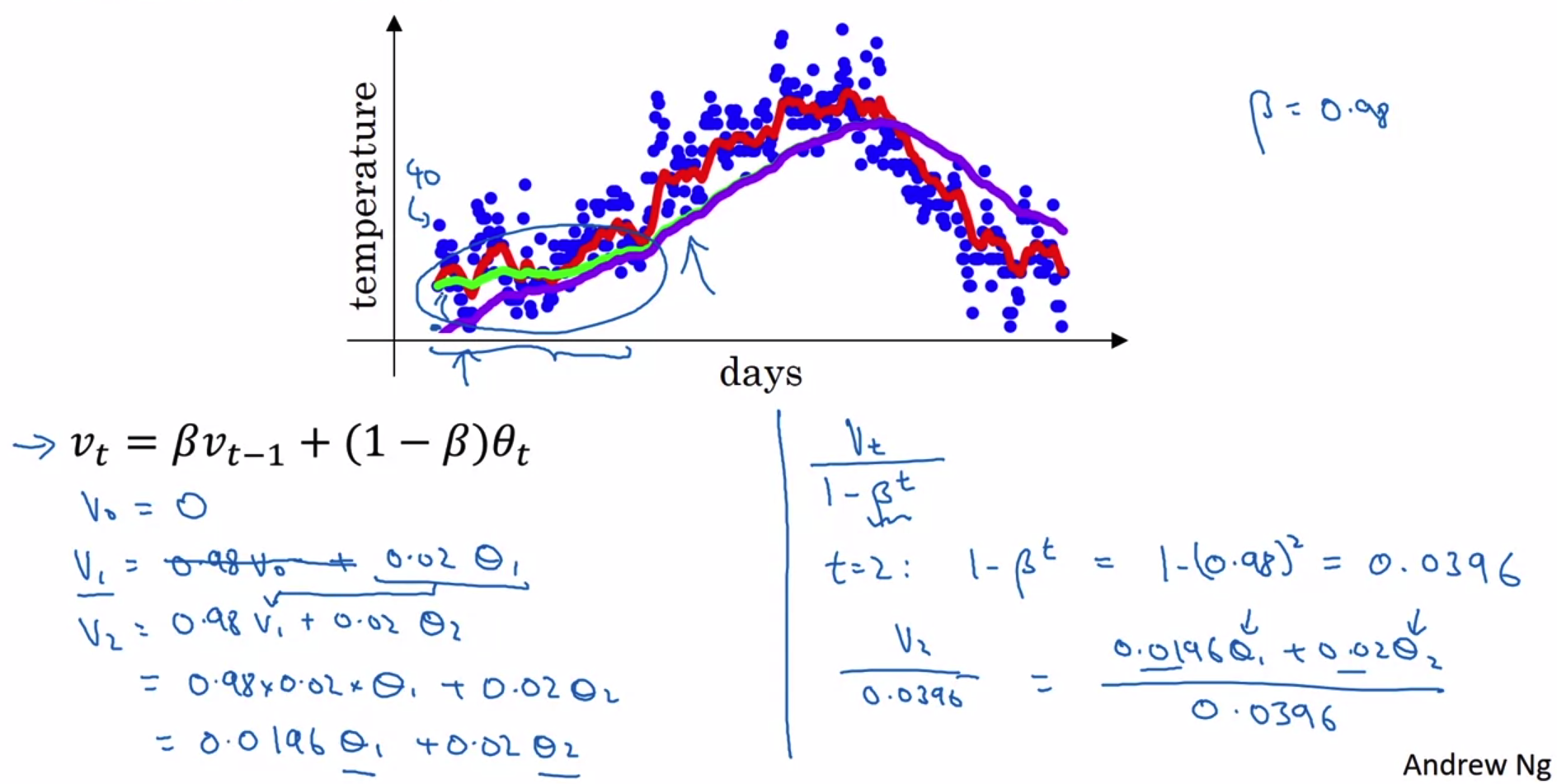
- 앞선 강의에 따르면 베타가 0.98일 때는 초록색 선과 같은 그래프가 나타나야 한다.
하지만 실제로는 초반 예측이 정확하지 않은 보라색 모양의 그래프 모양을 띠게 된다.
그 이유는 무엇일까? - 바로 초깃값 때문이다.
1일차부터 정보를 계산하기 때문에 0일차는 0으로 초기화된다.
결국 v1은 굉장히 작은 값이 되고, v1에 가중치를 곱하여 구한 v2도 굉장히 작은 값이 된다. - 따라서 bias correction을 통해 이런 문제를 해결할 수 있다.
여기서는 각 v_t를 (1-베타^t)로 나누어준다.
구체적인 예를 살펴보면 이렇게 나눗셈을 해줌으로써 가중치가 큰 값으로 바뀌게 된다는 것을 알 수 있다.
Bias correction 기법을 사용하면 초반부에 소실되는 값으로 인해 잘못 예측되는 결과를 빠르게 바로잡을 수 있다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 2주차' 카테고리의 다른 글
| Quiz & Programming Assignments (0) | 2022.11.13 |
|---|---|
| Optimization Algorithms(4) - Learning Rate Decay (0) | 2022.11.12 |
| Optimization Algorithms(3) - Gradient Descent (0) | 2022.11.10 |
| Optimization Algorithms(1) - Mini-batch (0) | 2022.11.08 |
1. Exponentially Weighted Averages (지수 가중 평균)
Temperature in London

- 영국의 1년 날씨를 날짜에 따라 표시한 그래프다.
전날과 오늘의 관계를 수식적으로 표현하여 그래프가 그려지는 양상을 예측하고자 한다.
Exponentially weighted averages

- V_t 로 표현된 수식이 Exponentially wieghted averages에 대한 수식이다.
이는 과거의 비중(가중치)을 베타로 표현하고 오늘의 비중을 세타로 표현하고 있다. - 따라서 베타가 아주 큰 경우에는 과거의 기록을 더 많이 반영하게 되므로 그래프가 완만한 초록색 선으로 표현된다.
대신 말 그대로 과거의 기록을 더 많이 반영하기 때문에 실제 데이터보다는 약간 우측에 치우치게 된다. - 반면 베타가 0.5인 경우에는 직전 하루만의 과거 정보를 다룬다는 의미가 된다.
즉 어제와 오늘의 정보를 반반 이용하겠다는 뜻이므로 아주 촘촘한 노란색 그래프로 표현된다.
이때는 변화에 굉장히 예민하다고 볼 수 있다.
2. Understanding Exponenetailly Weighted Averages
Exponentailly weighted averages

- 그림의 우측 상단 두 그래프를 먼저 살펴보자.
위의 그래프는 100일간의 기온을 x로 표시한 것이고, 아래의 그래프는 그 기온에 곱해지는 계수를 지수함수꼴로 표현한 것이다.
우리는 두 그래프의 각 값을 곱하여 100일간의 평균 기온을 구할 수 있다. - 베타가 0.9인 경우 100일간의 평균 기온을 구하는 전개식을 확인할 수 있다.
이때 계수가 지니는 의미를 살펴보면 1/e값이 되는 지점을 구하면 된다.
예를 들어 0.9의 10승은 약 0.35로 1/e값에 근사한다.
즉, 10일이 지나면 원래의 가중치보다 1/3만큼으로 줄어든 가중치를 적용하게 된다는 뜻이다. - 전개식의 의미를 다시 생각해보면 각 온도에 곱해지는 계수는 1 또는 1에 아주 근사한 값을 갖는다.
그렇기 때문에 이를 Exponentially weighted averages라고 부른다.
Implementing exponentially weigthed averages
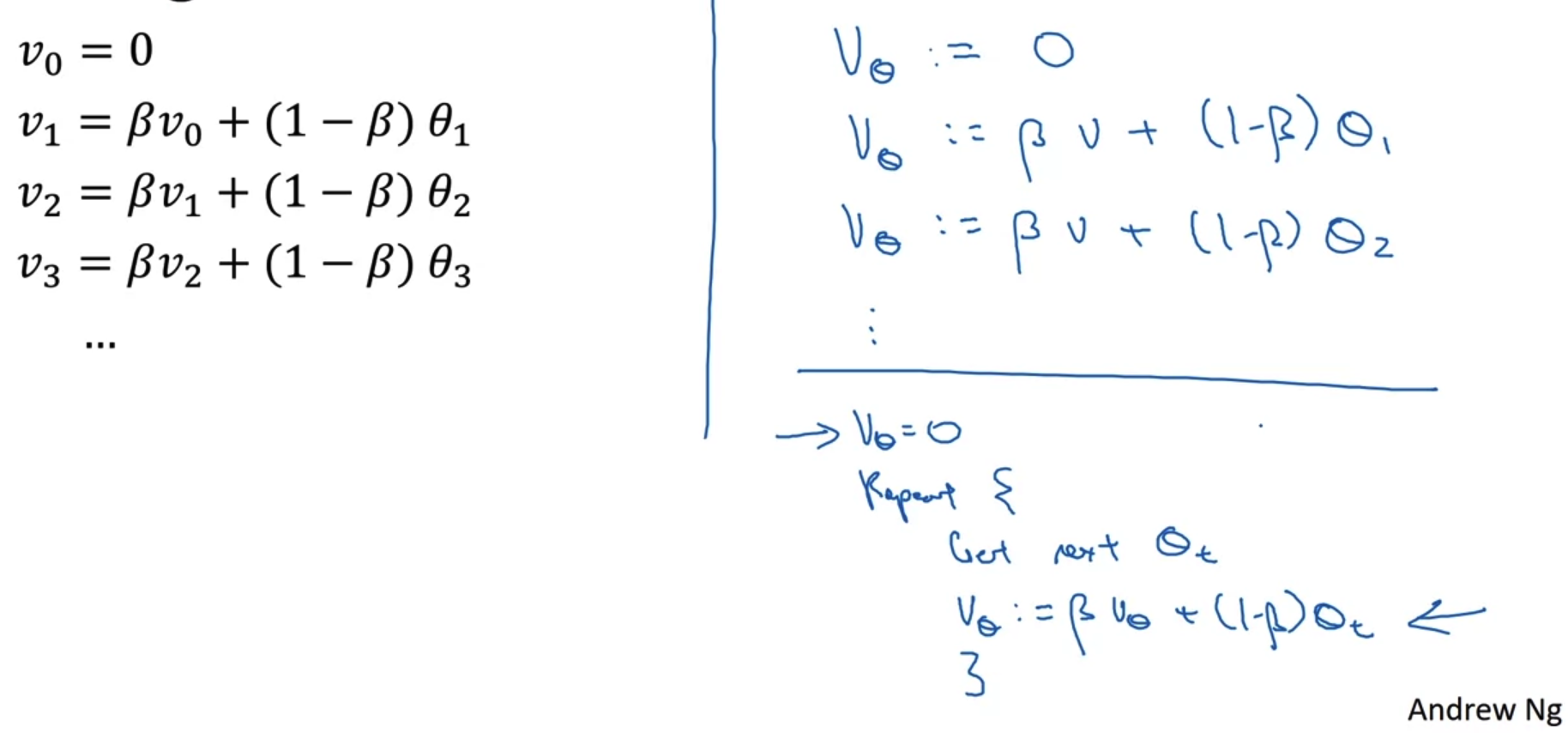
- exponentially weighted averages를 이용하는 방법은 위처럼 반복적인 식을 적용하는 것이다.
따라서 같은 식을 여러 번 반복해서 쓸 필요없이 반복문을 통해 간단히 계산할 수 있다. - 이런 방식은 모든 값들을 한꺼번에 메모리에 저장할 필요를 없어지게 함으로써 메모리 효율적이다.
그렇기 때문에 연산 속도도 매우 빠르다.
한 줄 짜리 코드로 표현할 수 있는만큼 구현하기 간편하다는 장점도 지닌다.
3. Bias Correction in Exponentially Weighted Averages
Bias correction

- 앞선 강의에 따르면 베타가 0.98일 때는 초록색 선과 같은 그래프가 나타나야 한다.
하지만 실제로는 초반 예측이 정확하지 않은 보라색 모양의 그래프 모양을 띠게 된다.
그 이유는 무엇일까? - 바로 초깃값 때문이다.
1일차부터 정보를 계산하기 때문에 0일차는 0으로 초기화된다.
결국 v1은 굉장히 작은 값이 되고, v1에 가중치를 곱하여 구한 v2도 굉장히 작은 값이 된다. - 따라서 bias correction을 통해 이런 문제를 해결할 수 있다.
여기서는 각 v_t를 (1-베타^t)로 나누어준다.
구체적인 예를 살펴보면 이렇게 나눗셈을 해줌으로써 가중치가 큰 값으로 바뀌게 된다는 것을 알 수 있다.
Bias correction 기법을 사용하면 초반부에 소실되는 값으로 인해 잘못 예측되는 결과를 빠르게 바로잡을 수 있다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 2주차' 카테고리의 다른 글
| Quiz & Programming Assignments (0) | 2022.11.13 |
|---|---|
| Optimization Algorithms(4) - Learning Rate Decay (0) | 2022.11.12 |
| Optimization Algorithms(3) - Gradient Descent (0) | 2022.11.10 |
| Optimization Algorithms(1) - Mini-batch (0) | 2022.11.08 |
