1. Learning Rate Decay
Learning Rate Decay
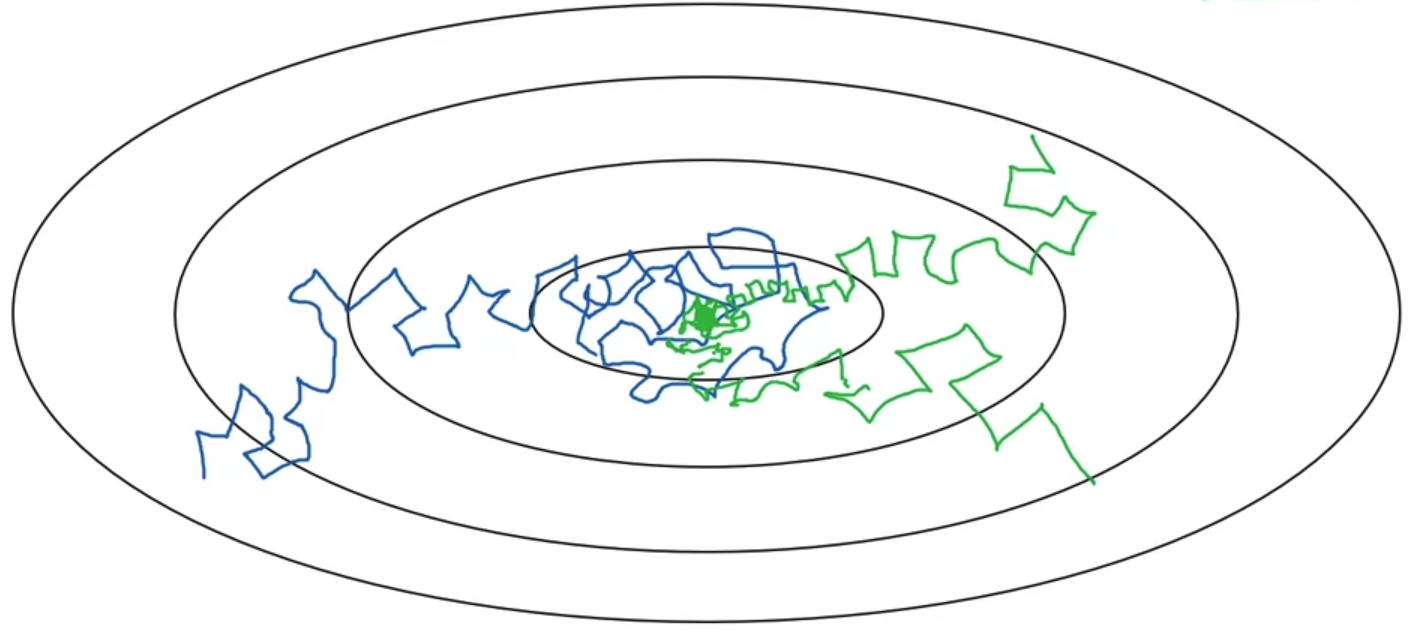
- 일반적인 mini-batch를 이용하면 파란색과 같은 그래프가 그려진다.
즉, 어느 정도의 noise를 포함한 형태이면서 절대 global minimum에 convergence(수렴)하지 못하고 주변을 배회(wandering)하게 된다. - 이를 해결하기 위해 제시된 것이 Learning Rate Decay로 학습이 진행됨에 따라 learning rate을 감소시키는 것을 말한다.
그러면 위 그림에서 초록색과 같은 그래프가 그려진다.
즉, 초반에는 큰 폭으로 학습이 진행되고 이후에는 그 폭을 줄이면서 global minimum에 convergence(수렴)하게 된다.
Leraning rate decay
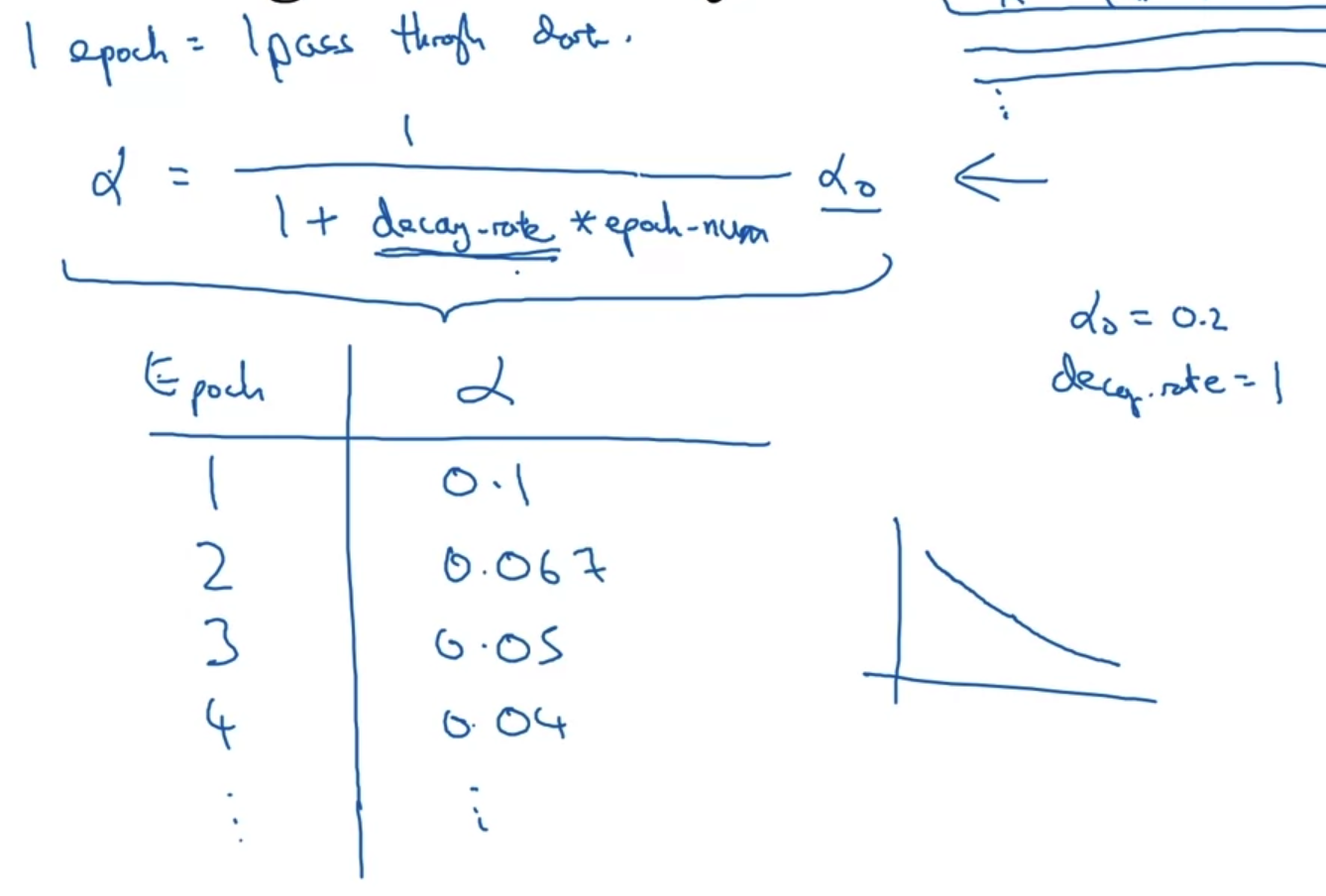
- epoch는 주어진 데이터를 한 번 다 학습하는 것을 말한다.
따라서 우리는 각 epoch에 따라 learning rate가 어떻게 바뀌는지 표로 확인할 수 있다. - 여기서 learning rate alpha는 decay rate과 alpha_0(initial learning rate)에 의해 조정된다.
따라서 decay rate과 alpha_0는 우리가 tuning 해야 하는 hypter parameter로 이해할 수 있다.
Other learning rate decay methods
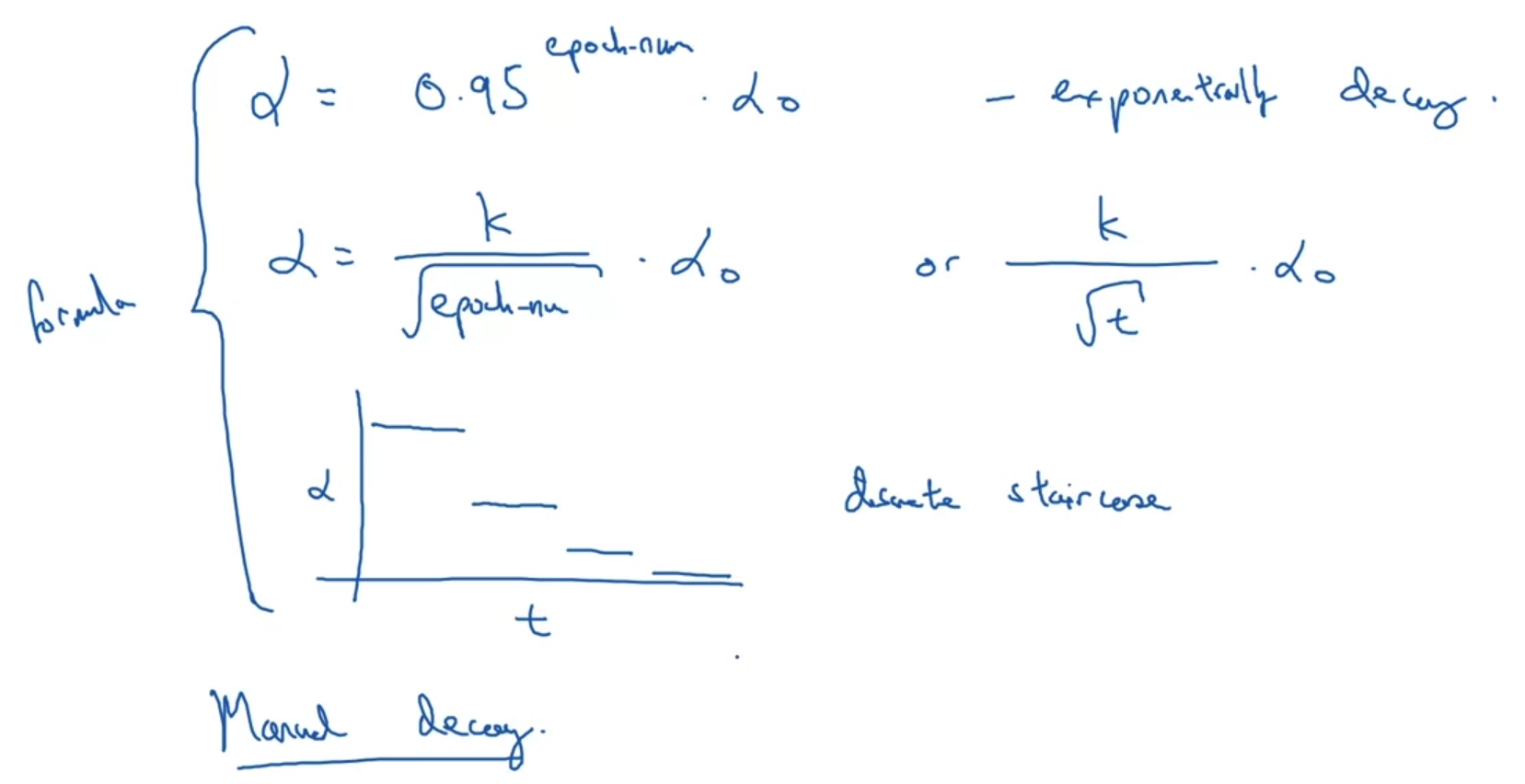
- 위에서 다룬 learning rate decay 외에도 다양한 방식들이 존재한다.
심지어 직접 decay를 적용하는 manual decay 방식도 있다. - 이렇게 여러 방식이 존재하는 learning rate decay는 학습의 속도를 향상시키는 좋은 기법이다.
2. The Problem of Local Optima
Local optima in neural networks

- gradient descent를 통해 최적의 값을 찾다보면 local minimum에 빠질 가능성이 있다.
물론 (가중치와 cost로 그린)그래프가 convex(아래로 볼록한) 형태라면 어느 지점에서 초기화를 하고 계산을 진행하더라도 상관이 없을 것이다.
위 예시에서는 올록볼록한 그래프가 제시되어 있다. - 이럴 경우 여러 지점의 local minimum이 존재하게 되고 각 지점에서의 gradient = 0이 된다.
즉, gradient가 0이 되는 순간 계산이 더 이상이 진행되지 않으므로 global minimum을 찾아갈 수 없게 된다. - 이런 포인트들을 오른쪽 그래프와 같이 본다면 마치 말의 안장(saddle)위의 한 점과 같은 모양이다.
따라서 이를 saddle point라고 부른다.
Problem of plateaus
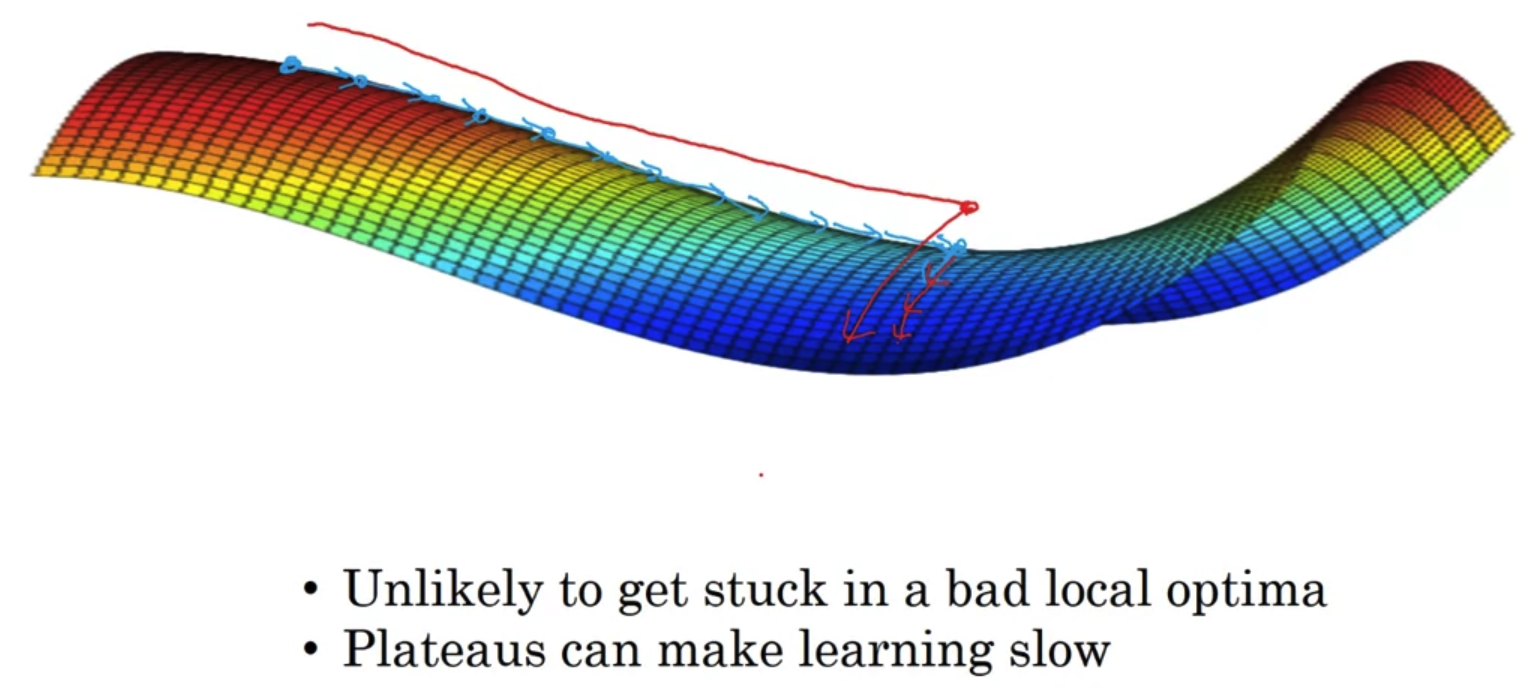
- 위에서처럼 그래프가 convex한 형태가 아닐 경우 여러 local optima에 갇힐 수 있다는 문제점이 있다.
그러나 사실 이는 그렇게 큰 문제는 아니다.
그럴 가능성이 그렇게 높지는 않기 때문이다. - 오히려 그보다는 그래프가 plateaus(고원, 평면)의 형태를 지닐 때 더 큰 문제가 발생한다.
이 경우 매 지점에서의 gradient가 0 혹은 0에 가까운 값이므로 학습이 진행되는 속도가 굉장히 느리다.
결국 아주 오랜 시간이 걸려서야 saddle point에 도착할 수 있고, 그 중에서도 global optima로 이동하는데까지 시간이 추가적으로 더 필요하다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 2주차' 카테고리의 다른 글
| Quiz & Programming Assignments (0) | 2022.11.13 |
|---|---|
| Optimization Algorithms(3) - Gradient Descent (0) | 2022.11.10 |
| Optimization Algorithms(2) - Exponentially Weighted Averages (0) | 2022.11.09 |
| Optimization Algorithms(1) - Mini-batch (0) | 2022.11.08 |
1. Learning Rate Decay
Learning Rate Decay

- 일반적인 mini-batch를 이용하면 파란색과 같은 그래프가 그려진다.
즉, 어느 정도의 noise를 포함한 형태이면서 절대 global minimum에 convergence(수렴)하지 못하고 주변을 배회(wandering)하게 된다. - 이를 해결하기 위해 제시된 것이 Learning Rate Decay로 학습이 진행됨에 따라 learning rate을 감소시키는 것을 말한다.
그러면 위 그림에서 초록색과 같은 그래프가 그려진다.
즉, 초반에는 큰 폭으로 학습이 진행되고 이후에는 그 폭을 줄이면서 global minimum에 convergence(수렴)하게 된다.
Leraning rate decay

- epoch는 주어진 데이터를 한 번 다 학습하는 것을 말한다.
따라서 우리는 각 epoch에 따라 learning rate가 어떻게 바뀌는지 표로 확인할 수 있다. - 여기서 learning rate alpha는 decay rate과 alpha_0(initial learning rate)에 의해 조정된다.
따라서 decay rate과 alpha_0는 우리가 tuning 해야 하는 hypter parameter로 이해할 수 있다.
Other learning rate decay methods

- 위에서 다룬 learning rate decay 외에도 다양한 방식들이 존재한다.
심지어 직접 decay를 적용하는 manual decay 방식도 있다. - 이렇게 여러 방식이 존재하는 learning rate decay는 학습의 속도를 향상시키는 좋은 기법이다.
2. The Problem of Local Optima
Local optima in neural networks

- gradient descent를 통해 최적의 값을 찾다보면 local minimum에 빠질 가능성이 있다.
물론 (가중치와 cost로 그린)그래프가 convex(아래로 볼록한) 형태라면 어느 지점에서 초기화를 하고 계산을 진행하더라도 상관이 없을 것이다.
위 예시에서는 올록볼록한 그래프가 제시되어 있다. - 이럴 경우 여러 지점의 local minimum이 존재하게 되고 각 지점에서의 gradient = 0이 된다.
즉, gradient가 0이 되는 순간 계산이 더 이상이 진행되지 않으므로 global minimum을 찾아갈 수 없게 된다. - 이런 포인트들을 오른쪽 그래프와 같이 본다면 마치 말의 안장(saddle)위의 한 점과 같은 모양이다.
따라서 이를 saddle point라고 부른다.
Problem of plateaus

- 위에서처럼 그래프가 convex한 형태가 아닐 경우 여러 local optima에 갇힐 수 있다는 문제점이 있다.
그러나 사실 이는 그렇게 큰 문제는 아니다.
그럴 가능성이 그렇게 높지는 않기 때문이다. - 오히려 그보다는 그래프가 plateaus(고원, 평면)의 형태를 지닐 때 더 큰 문제가 발생한다.
이 경우 매 지점에서의 gradient가 0 혹은 0에 가까운 값이므로 학습이 진행되는 속도가 굉장히 느리다.
결국 아주 오랜 시간이 걸려서야 saddle point에 도착할 수 있고, 그 중에서도 global optima로 이동하는데까지 시간이 추가적으로 더 필요하다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 2주차' 카테고리의 다른 글
| Quiz & Programming Assignments (0) | 2022.11.13 |
|---|---|
| Optimization Algorithms(3) - Gradient Descent (0) | 2022.11.10 |
| Optimization Algorithms(2) - Exponentially Weighted Averages (0) | 2022.11.09 |
| Optimization Algorithms(1) - Mini-batch (0) | 2022.11.08 |
