목차
1. Optimization Algorithms (Quiz)
- minibatch, layer, example에 대한 notation
- 각각 { }, [ ], ( ) 기호를 사용한다.
- vectorization
- Batch gradient descent는 한꺼번에 모든 데이터를 묶어 학습하겠다는 것이다.
따라서 memory의 문제만 없다면 vectorization을 가장 많이 수행하는 학습법일 것이다. - 그러나 batch gradient descent는 progress를 진행하기 전에 전체 training set을 처리해야 한다는 문제점이 있다.
- 한편 stochastic gradient descent는 여러 example을 vectorization 할 수 없다는 단점이 있다.
- Batch gradient descent는 한꺼번에 모든 데이터를 묶어 학습하겠다는 것이다.
- iteration - cost(J) graph
- 위아래로 요동치는 듯한 형태의 그래프는 mini-batch를 이용했을 때라면 당연한 것이다.
- 그러나 Batch size로 학습을 했는데 위아래로 요동치는 그래프가 그려졌다면 정상적인 학습이 이루어지지 않은 것이라 볼 수 있다.
- Exponentially weighted averages
- 주어진 조건에 따라 계산하는 문제가 출제된다.
- 위 계산에 bias correction을 적용도 해야 한다.
bias correction은 기존 v 값에 1-beta^t 를 나눠줌으로써 구할 수 있다. - beta는 과거 정보를 반영하는 비율, 1-beta는 현재 정보를 반영하는 비율로 이해할 수 있다.
beta가 커지면 커질수록 과거의 정보를 많이 반영함으로써 부드러운 형태이면서도 원래 데이터보다 오른쪽으로 치우친 모양의 그래프를 그리게 된다.
반대로 beta가 작아지면 과거의 정보를 적게 반영함으로써 원래 데이터를 잘 예측하는 형태이지만 위아래로 삐쭉삐쭉한 형태의 그래프를 그리게 된다.
- Learning rate decay
- learning rate decay로 사용되는 수식과 그렇지 않은 수식을 비교한다.
사용될 수 있는 수식들은 기본적으로 t의 값이 커짐에 따라 계산 결과가 점점 작아지는 형태다.
즉, 학습이 진행됨에 따라 learning rate가 줄어드는 구조이다. - 반대로 사용될 수 없는 수식은 t의 값이 커짐에 따라 그 계산 결과가 점점 커지는(발산하는) 형태다.
- learning rate decay로 사용되는 수식과 그렇지 않은 수식을 비교한다.
- Graident descent with Momentum
- Momentum은 moving average(이동 평균)을 이용하는 방식으로 exponentially weigthed bias를 적용하는 것과 동일하다.
- 따라서 beta의 값이 커질수록 smooth한 형태의 그래프가 나타난다.
- 이는 gradient descent 과정에서 oscilliation을 줄여주고 학습 속도를 높여준다.
- Optimization Adam
- Adam은 momentum과 RMSprop의 장점을 결합한 최적화 기법이다.
- Adam에 사용되는 변수 alpha는 tuning이 필요한 hyper parameter이다.
- 기본적으로 beta_1, beta_2, epsilon은 각각 0.9, 0.999, e-8이 default 값이다.
2. Optimization Methods (Programming Assignment)
2.1. Gradient Descent
update parameters with gradient descent
parameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate * grads['dW' + str(l)]
parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate * grads['db' + str(l)]- 딕셔너리에 저장되어 있는 W(가중치)와 b(편향)를 update하는 방식은 위와 같다.
기존의 값에 'learning rate와 gradient를 곱한 값'을 뺌으로써 값을 업데이트 할 수 있다.
Batch Gradient Descent
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost
cost_total = compute_cost(a, Y) # Cost for m training examples
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters
parameters = update_parameters(parameters, grads)
# Compute average cost
cost_avg = cost_total / mStochastic Gradient Descent
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
cost_total = 0
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost_total += compute_cost(a, Y[:,j]) # Cost for one training example
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters
parameters = update_parameters(parameters, grads)
# Compute average cost
cost_avg = cost_total / m- Batch gradient descent와 달리 한 epoch를 도는 동안 한 개의 example만을 가지고 학습하는 것을 알 수 있다.
X[ : , j ] 와 [ : , j ] 는 한 개의 열을 가져온다는 뜻이다.
input X는 여러 개의 example이 hidden size에 맞추어 열벡터로 바뀐 것이 합쳐진 형태이므로,
X의 shape이 ( hidden size, example number ) 가 되고 여기서 각 example을 추출해내는 것으로 이해할 수 있다. - 이렇게 함으로써 SGD는 oscillation을 보이지만(noise가 심하지만) 대신 학습 속도가 빠르다는 장점이 있다.
2.2. Mini-Batch Gradient Descent
random_mini_batches
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1, m))
inc = mini_batch_size
# Step 2 - Partition (shuffled_X, shuffled_Y).
num_complete_minibatches = math.floor(m / mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
for k in range(0, num_complete_minibatches):
# (approx. 2 lines)
# YOUR CODE STARTS HERE
mini_batch_X = shuffled_X[:, k*mini_batch_size:k*mini_batch_size+mini_batch_size]
mini_batch_Y = shuffled_Y[:, k*mini_batch_size:k*mini_batch_size+mini_batch_size]
# YOUR CODE ENDS HERE
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# For handling the end case (last mini-batch < mini_batch_size i.e less than 64)
if m % mini_batch_size != 0:
#(approx. 2 lines)
# mini_batch_X =
# mini_batch_Y =
# YOUR CODE STARTS HERE
mini_batch_X = shuffled_X[:,m-(m-inc*(m//inc)):]
mimi_batch_Y = shuffled_Y[:,m-(m-inc*(m//inc)):]
# YOUR CODE ENDS HERE
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)- 우선은 shuffle부터 이해해야 한다.
mini-batch 단위로 example을 가져오기 전에 기존의 training example을 섞는 과정이다.
여기서 주목할 점은 [ : , permutation ] 에서 permutation이 list라는 것이다. - np.random.permutation(int)를 사용하면 0부터 int-1까지의 숫자들을 random하게 나열해준다.
예를 들어 list(np.random.permutation(3)) = [0, 2, 1] 이 되는 것이다.
이 리스트를 인덱스의 두 번째 인자로 주게 되면 각 열을 불러오게 된다.
즉 앞의 인덱스 : 는 모든 행을 불러오는 것이고 뒤의 인덱스 [0, 2, 1]은 0, 2, 1번 인덱스를 순서대로 불러오는 것이다.
따라서 기존의 shape과 example을 유지하되 그 열(example)의 순서만 random하게 섞을 수 있게 된다. - 다음은 training example을 mini batch size로 나누게 된다.
어차피 example의 행은 hidden size이므로 모든 행을 불러오면 된다.
그리고 example을 batch size로 묶어서 불러와야 하므로 "반복문 인덱스 * 배치 사이즈 : (반복문 인덱스 + 1) * 배치 사이즈"를 열에 대한 인덱스로 사용하면 된다. - 만약 example의 개수가 batch size로 딱 나누어 떨어지지 않는 경우 마지막에 추가 작업이 필요하다.
이때는 "example의 개수 - (example의 개수 - 배치 사이즈 * (example의 개수 // 배치 사이즈))"를 이용하면 된다.
전체 example 중에서 batch size만큼 묶을 수 있을 만큼 묶어서 쓰고 남는 데이터를 끝까지 묶는 것으로 이해할 수 있다.
2.3. Momentum
initialize velocity
for l in range(1, L + 1):
# YOUR CODE STARTS HERE
v["dW" + str(l)] = np.zeros(parameters["W" + str(l)].shape)
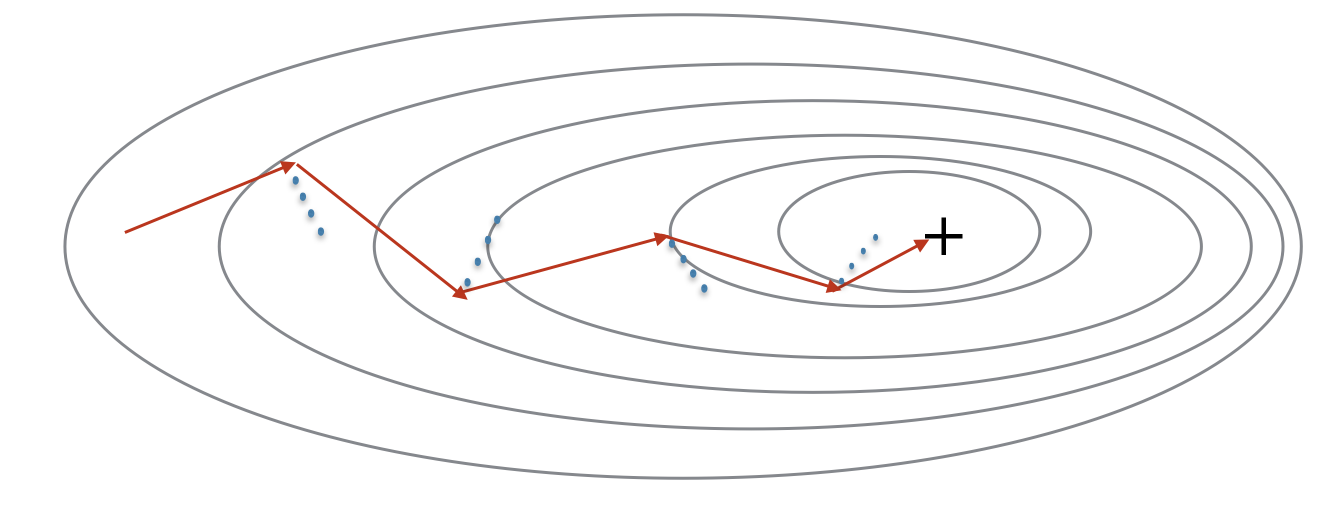
v["db" + str(l)] = np.zeros(parameters["b" + str(l)].shape)- 위 그래프에서 gradient는 방향을 정해주고 파란색 점은 그 velocity(속도)라고 생각할 수 있다.
이 velocity가 공이 굴러가는 속도에 영향을 주는 것으로 이해하면 된다. - 이 속도는 가중치와 편향을 미분한 값이 들어가는데 맨 처음에는 0으로 초기화해야 하므로 위와 같이 zeros_like를 사용하면 된다.
update parameters with momentum

for l in range(1, L + 1):
# YOUR CODE STARTS HERE
v["dW" + str(l)] = beta * v["dW" + str(l)] + (1-beta) * grads["dW" + str(l)]
v["db" + str(l)] = beta * v["db" + str(l)] + (1-beta) * grads["db" + str(l)]
parameters["W" + str(l)] -= learning_rate * v["dW" + str(l)]
parameters["b" + str(l)] -= learning_rate * v["db" + str(l)]- 위에 수식으로 정리된 것을 코드로 잘 구현하면 된다.
v_dW, v_db는 velocity에 대한 정보를 담고 있고 이는 momentum 방식을 이용해 계산된다.
그리고 실제 가중치가 업데이트 되는 것은 원래의 가중치에 'learning rate와 velocity를 곱한 값'을 빼주는 과정으로 진행된다. - momentum은 gradient descent를 smooth하게 만들어주기 위한 기법으로 이해할 수 있다.
이는 batch/mini-batch gradient descent에 적용될 수 있다.
2.4. Adam
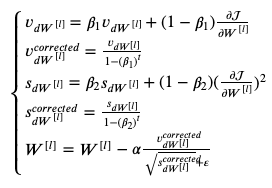
initialize adam
for l in range(1, L + 1):
v["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
v["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])
s["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
s["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])- 우선 exponentially weighted average of the gradient/squared graident가 담길 v와 s를 0으로 초기화한다.
- v는 momentum의 값을 저장하고 s는 RMSprop의 값을 저장한다.
update parameters with adam
for l in range(1, L + 1):
# YOUR CODE STARTS HERE
v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1-beta1) * grads["dW" + str(l)]
v["db" + str(l)] = beta1 * v["db" + str(l)] + (1-beta1) * grads["db" + str(l)]
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - beta1**t)
v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - beta1**t)
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1-beta2) * (grads["dW" + str(l)]**2)
s["db" + str(l)] = beta2 * s["db" + str(l)] + (1-beta2) * (grads["db" + str(l)]**2)
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - beta2**t)
s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - beta2**t)
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
parameters["W" + str(l)] -= learning_rate * v_corrected["dW" + str(l)] / (np.sqrt(s_corrected["dW" + str(l)]) + epsilon)
parameters["b" + str(l)] -= learning_rate * v_corrected["db" + str(l)] / (np.sqrt(s_corrected["db" + str(l)]) + epsilon)
# YOUR CODE ENDS HERE- 위 수식의 다섯 개 식을 코드로 구현한 것은 위와 같다.
- 우선 Momentum에 쓰이는 방식을 그대로 구현하여 값을 저장한 것은 v, v_corrected가 된다.
그리고 RMSprop에 쓰이는 방식을 그대로 구현하여 값을 저장한 것은 s, s_corrected가 된다. - Adam은 Momentum의 분자와 RMSprop의 분모를 합친 형태이므로 각각 필요한 값을 불러와 분수형태로 취해주면 된다.
Summary
- Momentum은 일반적으로 유용하지만 learning rate이 낮거나 dataset이 simple한 경우 거의 효과가 없다.
- 그러나 Adam은 mini-batch gradient descent와 Momentum의 성능을 능가한다.
성능은 비슷하게 나올지라도 gradient가 수렴하는 속도가 월등히 빠르다. - Adam의 장점을 요약하면 다음과 같다.
- 상대적으로 적은 메모리를 사용한다.
- 일반적으로 hyper-parameter를 적게 tuning하더라도 성능이 좋다.
| optimization method | accuracy | cost shape |
| Graident descent | >71% | smooth |
| Momentum | >71% | smooth |
| Adam | >94% | smoother |
2.5. Learning Rate Decay and Scheduling
update_lr
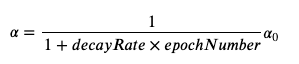
learning_rate = 1 / (1 + decay_rate * epoch_num) * learning_rate0- 학습이 진행됨에 따라 learning rate을 줄이는 방식을 learning rate decay라고 한다.
이런식으로 learning rate을 조정하는 것을 통틀어 scheduling이라고 부른다. - learning rate decay 공식을 코드로 구현한 것을 확인할 수 있다.
이후 decay에 대한 함수를 model의 parameter로 입력해주면 된다.
| Epoch Number | Learning Rate | Cost |
| 0 | 0.100000 | 0.701091 |
| 1000 | 0.000100 | 0.661884 |
| 2000 | 0.000050 | 0.658620 |
| 3000 | 0.000033 | 0.656765 |
| 4000 | 0.000025 | 0.655486 |
| 5000 | 0.000020 | 0.654514 |
- 결과를 보면 learning rate을 큰 값으로 초기화했음에도 불구하고 그 값이 빠르게 줄어드는 것을 확인할 수 있다.
- epoch이 작으면 위 현상이 문제되지 않지만, 만약 epoch이 크면 시간이 지남에 따라 optimization algorithm이 사실상 updating을 멈추게 된다.
이런 문제를 해결하기 위한 방식 중 하나가 learning rate를 일정 step마다 decay하는 것이고, 이를 'fixed interval scheduling'이라고 한다.
Fixed Interval Scheduling
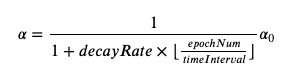
learning_rate = 1 / (1 + decay_rate * (epoch_num // time_interval)) * learning_rate0- Fixed Interval Scheduling은 이와 같이 분모의 epoch_num을 time_interval로 나눠줌으로써 learning rate이 지나치게 작아지는 것을 방지해준다.
epoch_num을 time_interval로 나눈 몫만 취하게 되므로 time_interval만큼은 학습이 진행되는 동안 같은 learning rate을 갖게 된다.
예를 들어 time_interval = 1,000인 경우 매 천 번 동안의 학습에서는 learning rate이 동일하고, 나눗셈의 몫이 감소하는 1001 번부터는 learning rate이 추가적으로 더 줄어들게 되는 것이다.
Summary
| optimization method | accuracy |
| Gradient descent | >94.6% |
| Momentum | >95.6% |
| Adam | 94% |
- Mini-batch GD와 Mini-batch GD에 momentum을 적용한 것은 Adam만 사용한 것보다 낮은 성능을 보인다.
그러나 learning rate decay가 적용되면 둘 다 학습 속도도 발라지고 Adam과 비슷한 성능을 낼 수 있게 된다. - Adam의 경우 정확도 측면에서는 다른 것들과 비슷하게 나타났지만 학습 속도가 훨씬 빠르다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 2주차' 카테고리의 다른 글
| Optimization Algorithms(4) - Learning Rate Decay (0) | 2022.11.12 |
|---|---|
| Optimization Algorithms(3) - Gradient Descent (0) | 2022.11.10 |
| Optimization Algorithms(2) - Exponentially Weighted Averages (0) | 2022.11.09 |
| Optimization Algorithms(1) - Mini-batch (0) | 2022.11.08 |
1. Optimization Algorithms (Quiz)
- minibatch, layer, example에 대한 notation
- 각각 { }, [ ], ( ) 기호를 사용한다.
- vectorization
- Batch gradient descent는 한꺼번에 모든 데이터를 묶어 학습하겠다는 것이다.
따라서 memory의 문제만 없다면 vectorization을 가장 많이 수행하는 학습법일 것이다. - 그러나 batch gradient descent는 progress를 진행하기 전에 전체 training set을 처리해야 한다는 문제점이 있다.
- 한편 stochastic gradient descent는 여러 example을 vectorization 할 수 없다는 단점이 있다.
- Batch gradient descent는 한꺼번에 모든 데이터를 묶어 학습하겠다는 것이다.
- iteration - cost(J) graph
- 위아래로 요동치는 듯한 형태의 그래프는 mini-batch를 이용했을 때라면 당연한 것이다.
- 그러나 Batch size로 학습을 했는데 위아래로 요동치는 그래프가 그려졌다면 정상적인 학습이 이루어지지 않은 것이라 볼 수 있다.
- Exponentially weighted averages
- 주어진 조건에 따라 계산하는 문제가 출제된다.
- 위 계산에 bias correction을 적용도 해야 한다.
bias correction은 기존 v 값에 1-beta^t 를 나눠줌으로써 구할 수 있다. - beta는 과거 정보를 반영하는 비율, 1-beta는 현재 정보를 반영하는 비율로 이해할 수 있다.
beta가 커지면 커질수록 과거의 정보를 많이 반영함으로써 부드러운 형태이면서도 원래 데이터보다 오른쪽으로 치우친 모양의 그래프를 그리게 된다.
반대로 beta가 작아지면 과거의 정보를 적게 반영함으로써 원래 데이터를 잘 예측하는 형태이지만 위아래로 삐쭉삐쭉한 형태의 그래프를 그리게 된다.
- Learning rate decay
- learning rate decay로 사용되는 수식과 그렇지 않은 수식을 비교한다.
사용될 수 있는 수식들은 기본적으로 t의 값이 커짐에 따라 계산 결과가 점점 작아지는 형태다.
즉, 학습이 진행됨에 따라 learning rate가 줄어드는 구조이다. - 반대로 사용될 수 없는 수식은 t의 값이 커짐에 따라 그 계산 결과가 점점 커지는(발산하는) 형태다.
- learning rate decay로 사용되는 수식과 그렇지 않은 수식을 비교한다.
- Graident descent with Momentum
- Momentum은 moving average(이동 평균)을 이용하는 방식으로 exponentially weigthed bias를 적용하는 것과 동일하다.
- 따라서 beta의 값이 커질수록 smooth한 형태의 그래프가 나타난다.
- 이는 gradient descent 과정에서 oscilliation을 줄여주고 학습 속도를 높여준다.
- Optimization Adam
- Adam은 momentum과 RMSprop의 장점을 결합한 최적화 기법이다.
- Adam에 사용되는 변수 alpha는 tuning이 필요한 hyper parameter이다.
- 기본적으로 beta_1, beta_2, epsilon은 각각 0.9, 0.999, e-8이 default 값이다.
2. Optimization Methods (Programming Assignment)
2.1. Gradient Descent
update parameters with gradient descent
parameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate * grads['dW' + str(l)]
parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate * grads['db' + str(l)]- 딕셔너리에 저장되어 있는 W(가중치)와 b(편향)를 update하는 방식은 위와 같다.
기존의 값에 'learning rate와 gradient를 곱한 값'을 뺌으로써 값을 업데이트 할 수 있다.
Batch Gradient Descent
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost
cost_total = compute_cost(a, Y) # Cost for m training examples
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters
parameters = update_parameters(parameters, grads)
# Compute average cost
cost_avg = cost_total / mStochastic Gradient Descent
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
cost_total = 0
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost_total += compute_cost(a, Y[:,j]) # Cost for one training example
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters
parameters = update_parameters(parameters, grads)
# Compute average cost
cost_avg = cost_total / m- Batch gradient descent와 달리 한 epoch를 도는 동안 한 개의 example만을 가지고 학습하는 것을 알 수 있다.
X[ : , j ] 와 [ : , j ] 는 한 개의 열을 가져온다는 뜻이다.
input X는 여러 개의 example이 hidden size에 맞추어 열벡터로 바뀐 것이 합쳐진 형태이므로,
X의 shape이 ( hidden size, example number ) 가 되고 여기서 각 example을 추출해내는 것으로 이해할 수 있다. - 이렇게 함으로써 SGD는 oscillation을 보이지만(noise가 심하지만) 대신 학습 속도가 빠르다는 장점이 있다.
2.2. Mini-Batch Gradient Descent
random_mini_batches
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1, m))
inc = mini_batch_size
# Step 2 - Partition (shuffled_X, shuffled_Y).
num_complete_minibatches = math.floor(m / mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
for k in range(0, num_complete_minibatches):
# (approx. 2 lines)
# YOUR CODE STARTS HERE
mini_batch_X = shuffled_X[:, k*mini_batch_size:k*mini_batch_size+mini_batch_size]
mini_batch_Y = shuffled_Y[:, k*mini_batch_size:k*mini_batch_size+mini_batch_size]
# YOUR CODE ENDS HERE
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# For handling the end case (last mini-batch < mini_batch_size i.e less than 64)
if m % mini_batch_size != 0:
#(approx. 2 lines)
# mini_batch_X =
# mini_batch_Y =
# YOUR CODE STARTS HERE
mini_batch_X = shuffled_X[:,m-(m-inc*(m//inc)):]
mimi_batch_Y = shuffled_Y[:,m-(m-inc*(m//inc)):]
# YOUR CODE ENDS HERE
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)- 우선은 shuffle부터 이해해야 한다.
mini-batch 단위로 example을 가져오기 전에 기존의 training example을 섞는 과정이다.
여기서 주목할 점은 [ : , permutation ] 에서 permutation이 list라는 것이다. - np.random.permutation(int)를 사용하면 0부터 int-1까지의 숫자들을 random하게 나열해준다.
예를 들어 list(np.random.permutation(3)) = [0, 2, 1] 이 되는 것이다.
이 리스트를 인덱스의 두 번째 인자로 주게 되면 각 열을 불러오게 된다.
즉 앞의 인덱스 : 는 모든 행을 불러오는 것이고 뒤의 인덱스 [0, 2, 1]은 0, 2, 1번 인덱스를 순서대로 불러오는 것이다.
따라서 기존의 shape과 example을 유지하되 그 열(example)의 순서만 random하게 섞을 수 있게 된다. - 다음은 training example을 mini batch size로 나누게 된다.
어차피 example의 행은 hidden size이므로 모든 행을 불러오면 된다.
그리고 example을 batch size로 묶어서 불러와야 하므로 "반복문 인덱스 * 배치 사이즈 : (반복문 인덱스 + 1) * 배치 사이즈"를 열에 대한 인덱스로 사용하면 된다. - 만약 example의 개수가 batch size로 딱 나누어 떨어지지 않는 경우 마지막에 추가 작업이 필요하다.
이때는 "example의 개수 - (example의 개수 - 배치 사이즈 * (example의 개수 // 배치 사이즈))"를 이용하면 된다.
전체 example 중에서 batch size만큼 묶을 수 있을 만큼 묶어서 쓰고 남는 데이터를 끝까지 묶는 것으로 이해할 수 있다.
2.3. Momentum
initialize velocity

for l in range(1, L + 1):
# YOUR CODE STARTS HERE
v["dW" + str(l)] = np.zeros(parameters["W" + str(l)].shape)
v["db" + str(l)] = np.zeros(parameters["b" + str(l)].shape)- 위 그래프에서 gradient는 방향을 정해주고 파란색 점은 그 velocity(속도)라고 생각할 수 있다.
이 velocity가 공이 굴러가는 속도에 영향을 주는 것으로 이해하면 된다. - 이 속도는 가중치와 편향을 미분한 값이 들어가는데 맨 처음에는 0으로 초기화해야 하므로 위와 같이 zeros_like를 사용하면 된다.
update parameters with momentum

for l in range(1, L + 1):
# YOUR CODE STARTS HERE
v["dW" + str(l)] = beta * v["dW" + str(l)] + (1-beta) * grads["dW" + str(l)]
v["db" + str(l)] = beta * v["db" + str(l)] + (1-beta) * grads["db" + str(l)]
parameters["W" + str(l)] -= learning_rate * v["dW" + str(l)]
parameters["b" + str(l)] -= learning_rate * v["db" + str(l)]- 위에 수식으로 정리된 것을 코드로 잘 구현하면 된다.
v_dW, v_db는 velocity에 대한 정보를 담고 있고 이는 momentum 방식을 이용해 계산된다.
그리고 실제 가중치가 업데이트 되는 것은 원래의 가중치에 'learning rate와 velocity를 곱한 값'을 빼주는 과정으로 진행된다. - momentum은 gradient descent를 smooth하게 만들어주기 위한 기법으로 이해할 수 있다.
이는 batch/mini-batch gradient descent에 적용될 수 있다.
2.4. Adam
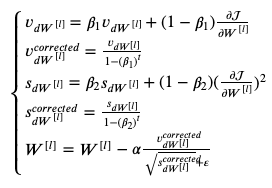
initialize adam
for l in range(1, L + 1):
v["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
v["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])
s["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
s["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])- 우선 exponentially weighted average of the gradient/squared graident가 담길 v와 s를 0으로 초기화한다.
- v는 momentum의 값을 저장하고 s는 RMSprop의 값을 저장한다.
update parameters with adam
for l in range(1, L + 1):
# YOUR CODE STARTS HERE
v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1-beta1) * grads["dW" + str(l)]
v["db" + str(l)] = beta1 * v["db" + str(l)] + (1-beta1) * grads["db" + str(l)]
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - beta1**t)
v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - beta1**t)
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1-beta2) * (grads["dW" + str(l)]**2)
s["db" + str(l)] = beta2 * s["db" + str(l)] + (1-beta2) * (grads["db" + str(l)]**2)
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - beta2**t)
s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - beta2**t)
# YOUR CODE ENDS HERE
# YOUR CODE STARTS HERE
parameters["W" + str(l)] -= learning_rate * v_corrected["dW" + str(l)] / (np.sqrt(s_corrected["dW" + str(l)]) + epsilon)
parameters["b" + str(l)] -= learning_rate * v_corrected["db" + str(l)] / (np.sqrt(s_corrected["db" + str(l)]) + epsilon)
# YOUR CODE ENDS HERE- 위 수식의 다섯 개 식을 코드로 구현한 것은 위와 같다.
- 우선 Momentum에 쓰이는 방식을 그대로 구현하여 값을 저장한 것은 v, v_corrected가 된다.
그리고 RMSprop에 쓰이는 방식을 그대로 구현하여 값을 저장한 것은 s, s_corrected가 된다. - Adam은 Momentum의 분자와 RMSprop의 분모를 합친 형태이므로 각각 필요한 값을 불러와 분수형태로 취해주면 된다.
Summary
- Momentum은 일반적으로 유용하지만 learning rate이 낮거나 dataset이 simple한 경우 거의 효과가 없다.
- 그러나 Adam은 mini-batch gradient descent와 Momentum의 성능을 능가한다.
성능은 비슷하게 나올지라도 gradient가 수렴하는 속도가 월등히 빠르다. - Adam의 장점을 요약하면 다음과 같다.
- 상대적으로 적은 메모리를 사용한다.
- 일반적으로 hyper-parameter를 적게 tuning하더라도 성능이 좋다.
| optimization method | accuracy | cost shape |
| Graident descent | >71% | smooth |
| Momentum | >71% | smooth |
| Adam | >94% | smoother |
2.5. Learning Rate Decay and Scheduling
update_lr
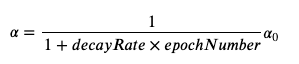
learning_rate = 1 / (1 + decay_rate * epoch_num) * learning_rate0- 학습이 진행됨에 따라 learning rate을 줄이는 방식을 learning rate decay라고 한다.
이런식으로 learning rate을 조정하는 것을 통틀어 scheduling이라고 부른다. - learning rate decay 공식을 코드로 구현한 것을 확인할 수 있다.
이후 decay에 대한 함수를 model의 parameter로 입력해주면 된다.
| Epoch Number | Learning Rate | Cost |
| 0 | 0.100000 | 0.701091 |
| 1000 | 0.000100 | 0.661884 |
| 2000 | 0.000050 | 0.658620 |
| 3000 | 0.000033 | 0.656765 |
| 4000 | 0.000025 | 0.655486 |
| 5000 | 0.000020 | 0.654514 |
- 결과를 보면 learning rate을 큰 값으로 초기화했음에도 불구하고 그 값이 빠르게 줄어드는 것을 확인할 수 있다.
- epoch이 작으면 위 현상이 문제되지 않지만, 만약 epoch이 크면 시간이 지남에 따라 optimization algorithm이 사실상 updating을 멈추게 된다.
이런 문제를 해결하기 위한 방식 중 하나가 learning rate를 일정 step마다 decay하는 것이고, 이를 'fixed interval scheduling'이라고 한다.
Fixed Interval Scheduling
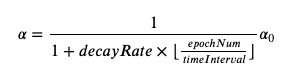
learning_rate = 1 / (1 + decay_rate * (epoch_num // time_interval)) * learning_rate0- Fixed Interval Scheduling은 이와 같이 분모의 epoch_num을 time_interval로 나눠줌으로써 learning rate이 지나치게 작아지는 것을 방지해준다.
epoch_num을 time_interval로 나눈 몫만 취하게 되므로 time_interval만큼은 학습이 진행되는 동안 같은 learning rate을 갖게 된다.
예를 들어 time_interval = 1,000인 경우 매 천 번 동안의 학습에서는 learning rate이 동일하고, 나눗셈의 몫이 감소하는 1001 번부터는 learning rate이 추가적으로 더 줄어들게 되는 것이다.
Summary
| optimization method | accuracy |
| Gradient descent | >94.6% |
| Momentum | >95.6% |
| Adam | 94% |
- Mini-batch GD와 Mini-batch GD에 momentum을 적용한 것은 Adam만 사용한 것보다 낮은 성능을 보인다.
그러나 learning rate decay가 적용되면 둘 다 학습 속도도 발라지고 Adam과 비슷한 성능을 낼 수 있게 된다. - Adam의 경우 정확도 측면에서는 다른 것들과 비슷하게 나타났지만 학습 속도가 훨씬 빠르다.
출처: Coursera, Improving Deep Neural Networks, DeepLearning.AI
'Improving Deep Neural Networks > 2주차' 카테고리의 다른 글
| Optimization Algorithms(4) - Learning Rate Decay (0) | 2022.11.12 |
|---|---|
| Optimization Algorithms(3) - Gradient Descent (0) | 2022.11.10 |
| Optimization Algorithms(2) - Exponentially Weighted Averages (0) | 2022.11.09 |
| Optimization Algorithms(1) - Mini-batch (0) | 2022.11.08 |
