4.7.1. 먼저 결론
폭주 판정의 결론은 거의 변하지 않는다.
- 단, 특수한 경우 미묘한 문제가 발생한다.

4.7.2. 대각까지는 못하더라도 - 요르단표준형
대각화할 수 없는 정방행렬 A라도 대각에 가까운 요르단 표준형이라면 반드시 변환할 수 있다.
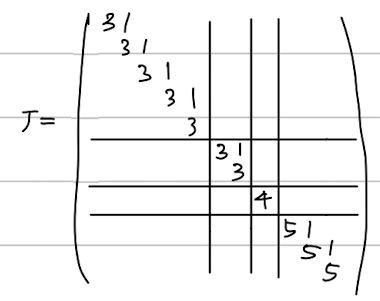
- 블록대각(블록정방행렬이고, 대각블록 이외는 모두 0)
- 대각블록의 성질
- 대각성분에 같은 수가 나열
- 하나 오른쪽 위는 1이 비스듬히 늘어섬
- 위와 같은 것을 요르단 셀이라고 한다. 여기서는 크기 5, 2, 1, 3 짜리 요르단 셀이 늘어서 있다.
행렬 A를 변환하여 만들 수 있는 요르단 표준형은 한 가지이다.
4.7.3. 요르단 표준형의 성질
폭주 판정과 관련이 있다.
- 고윳값, 고유벡터의 모양이 보인다.
- 거듭제곱을 구체적으로 계산할 수 있다.
요르단 표준형의 고윳값
- 대각성분이 고윳값 λ
- 대각성분의 λ 개수가 고윳값 λ 몇 중해인지에 대응
- 대각성분이 λ인 요르단 셀의 개수가 고윳값 λ에 선형독립인 고유벡터 개수(기하적 중복도)에 대응
- 따라서 고윳값에 중해가 없으면 대각화할 수 있다.
요르단 표준형의 거듭제곱

- 요르단표준형 전체에 대해서는 각 요르단 셀의 제곱을 구하고 합쳐주면 된다.
요르단 표준형이 아닌 정방행렬A의 거듭제곱 A^t

4.7.4. 요르단 표준형으로 초깃값 문제를 풀다(폭주 판정의 최종 결론)
어떤 정방행렬 A라도 요르단 표준형으로 변환할 수 있다. 이후 각 서브 시스템에 대해
- 서브 시스템 중 하나라도 폭주의 위험이 있다면 전체도 폭주의 위험이 있다.
- 서비 시스템이 모두 폭주하지 않는다면 전체도 폭주하지 않는다.
이산시간 시스템

- λ의 절댓값이 1보다 크면 폭주한다.
- λ의 절댓값이 1인 경우는 B의 크기 m 나름이다.
- m이 2 이상이면 폭주한다.
- m이 1이면폭주하지 않는다.
- λ의 절댓값이 1보다 작으면 폭주하지 않는다.
요르단 표준형이 아닌 일반 정방행렬 A에 대해 x(t) = Ax(t-1)의 폭주 판정
- λ의 절댓값이 1보다 큰 고윳값 λ를 하나라도 지니면 폭주
- 모든 고윳값 λ의 절댓값이 1보다 작으면 폭주하지 않는다.
- 모든 고윳값 λ의 절댓값이 1 이하이지만, λ의 절댓값이 1인 경우도 포함되면 고윳값만으로 판정할 수 없다.
- λ의 절댓값이 1인 경우
- 고윳값 λ은 k중해(k >= 2)
- 고윳값 λ에 대응하는 고유벡터에서 선형독립인 것을 k개 취할 수 없다.
- 위 세 조건을 모두 충족하지 않는 경우에만 폭주하지 않는다.
연속시간 시스템

- Re λ > 0 이면 폭주한다.
- Re λ = 0인 경우 B의 크기 m 나름이다.
- m >= 2이면 폭주한다.
- m = 1이면 폭주하지 않는다.
- Re λ < 0이면 폭주하지 않는다.
이하 나머지 조건은 이산시간의 경우와 동일하다.
4.7.5. 요르단 표준형 구하는 법
가령 구했다면

- 곱을 반복하여 0이 된다는 벡터 계열
- λ는 요르단 셀의 대각성분에 대응
- 한 계산의 흐름이 요르단 셀 한 개와 대응
- 계열의 일치가 요르단 셀의 크기에 대응
정리하면 1. A의 고윳값 λ를 구한다. 2. (A-λI)를 반복하여 곱하면 0이 되는 벡터 p를 구한다.
이와 같은 p를 일반화 고유벡터라고 한다.
- 0 자신은 예외로 일반화 고유벡터라고 부르지 않는다.
구하는 법

- 계열의 각 한 개가 요르단 셀 각 한개에 대응하고, 계열의 길이가 요르단 셀 크기와 대응한다.
- Ki = dim Ker(A - 3I)^i를 i = 1,2,3, ... 으로 구하면 후보 중 정답을 추릴 수 있다.
- 완성된 p1, ... p11을 나열하여 정방행렬 P = (p1, ... , p11)를 만들면 P^-1AP가 요르단 표준형이 된다.
4.7.6. 요르단 표준형으로 변환할 수 있는 것의 증명
n차 정방행렬 A에 대해 p^-1AP가 요르단 표준형이 되도록 하는 좋은 정칙행렬 P가 반드시 있다.
n개의 n차원벡터 p1, ... ,pn에 대해
- p1, ... , pn은 여러 계열을 이룬다.
- p1, ... , pn은 선형독립이다. 즉, 기저를 이룬다.
두 조건을 만족 시키면 된다.
유파 W(λ) 만들기
- 정확히는 일반화 고유공간이라고 칭한다. ker(A-λI)를 뜻한다.
- (A-λI)를 몇 번 곱하면 0이 되는 n차원 벡터의 집합
- 0 자신도 유파에 속한다고 간주
- 어느 유파에도 속하지 않는 벡터는 후보 자격이 없다.
유파의 특징
- 0 이외의 멤버가 있는 유파 W(λ)는 λ가 A의 고윳값인 것뿐이다.
- 둘 이상의 유파에 동시에 속할 수는 없다.
좋은 행렬 P로 Z를 변환하면 F라는 특징적인행렬이 될 수 있다.
- 블록 대각행렬
- 대각블록에서 대각성분의 하나 오른쪽 위에 1이 비스듬히 나열
- 한 개의 계열이 하나의 대각블록에 대응
- 계열의 길이가 대각블록의 크기에 대응
- 고윳값이 0인 요르단 표준형의 모양
출처: 히라오카 카즈유키, 호리 겐, 『프로그래머를 위한 선형대수』, 이창신, 길벗, 2017.
'프로그래머를 위한 선형대수 > 4장' 카테고리의 다른 글
| 4.6. 연속시간 시스템 (0) | 2022.09.15 |
|---|---|
| 4.5. 고윳값, 고유벡터 (0) | 2022.09.15 |
| 4.4. 대각화할 수 있는 경우 (0) | 2022.09.15 |
| 4.2. 1차원의 경우 / 4.3. 대각행렬의 경우 (0) | 2022.09.14 |
| 4.1. 문제 설정: 안정성 (0) | 2022.09.13 |
