최근(2023.09)에 나온 논문을 읽어보고 간단히 정리했습니다.
혹시 부족하거나 잘못된 내용이 있다면 댓글 부탁드립니다 🙇♂️
[MIT]
사전학습된 LLM의 context size를 확장하는 efficient fine-tuning 기법, LongLoRA.
sparse local attention 방식 중 하나로 shift shoft attention(S^2-Attn)를 제안하고,
trainable embedding & normalization을 통해 computational cost를 대폭 줄이면서도 기존 모델에 준하는 성능을 보임.
Fine-tugning을 위한 3K 이상의 long context question-answer pair dataset, LongQA 공개.
배경
LLM들은 이미 사전 정의된 context size를 갖고 있습니다.
하지만 이로 인해 LLM을 다양한 분야에 접목시키기 어렵다는 문제가 발생합니다.
예를 들어 2048개 토큰을 최대 context size로 지니는 LLaMA의 경우, 이를 초과하는 길이의 문서를 요약하는 등의 작업은 제대로 처리할 수 없게 되는 것이죠.
그래서 이 context window를 확장하고자 하는 다양한 시도들이 있었지만, transformer의 아키텍쳐는 context size의 quadratic하게 비례하는 연산량을 갖는다는 특징이 문제로 지적되었습니다.
엄청 단순하게만 생각해보면 context를 두 배로 확장하기 위해서는 네 배의 GPU 자원이 필요하게 되는 것입니다.
이런 한계를 극복하기 위해서 self-attention을 개선하여 연산량은 줄이되 기존 full attention만큼의 성능을 유지할 수 있도록 하는 시도도 끊임없이 이뤄지고 있습니다.
본 논문에서 제시하는 LongLoRA 역시 같은 맥락의 연구 결과입니다.
LongLoRA
shift short attention
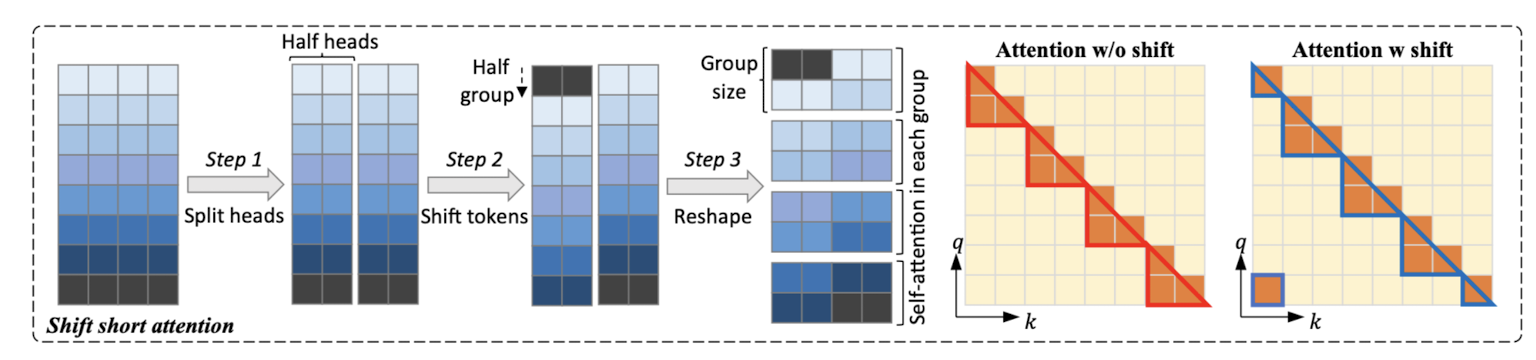
본 논문에서는 shift short attention을 사용하고 있습니다.
이는 short attention 방식에 shift를 적용한 것으로 계산 과정은 위와 같이 시각화될 수 있습니다.
1) 우선 feature를 head 차원에 대해 반으로 쪼갭니다.
만약 8개의 head가 있었다면 이를 4개로 쪼개는 것입니다.
2) head chunk 중 하나가 그룹 사이즈의 절반만큼 이동합니다.
위 예시에서는 4개의 head가 2개로 쪼개지며 각 그룹은 2개의 head로 구성됩니다. 따라서 이것의 절반인 1(토큰)만큼 이동한 것으로 이해할 수 있습니다.
만약 head가 8개인 구조였다면 2(토큰)만큼 이동했을 것입니다.
3) 마지막으로 토큰들을 이번엔 배치 단위로 쪼개어 그룹을 형성합니다.
위 예시에서는 토큰이 8개인 상황을 다루고 있는데, 이때 각 그룹은 두 개의 토큰으로 구성됩니다. 즉 배치 사이즈가 2인 예시입니다.
이러한 방식으로 계산을 진행하는 shif short attention은 기존의 self-attention이 모든 토큰에 대해 계산하는 것과 달리, 각 배치 그룹마다 계산을 하게 되어 있고, shift를 통해 그룹 간 information이 전달(flow)되는 것으로 이해할 수 있습니다.
Architecture
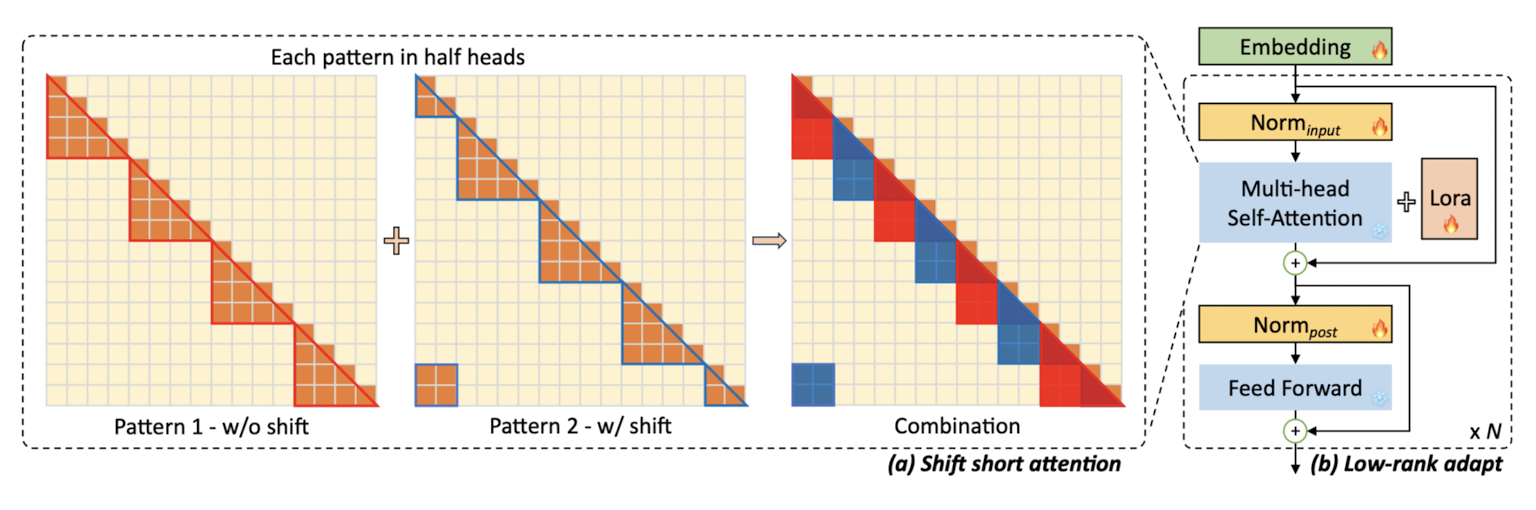
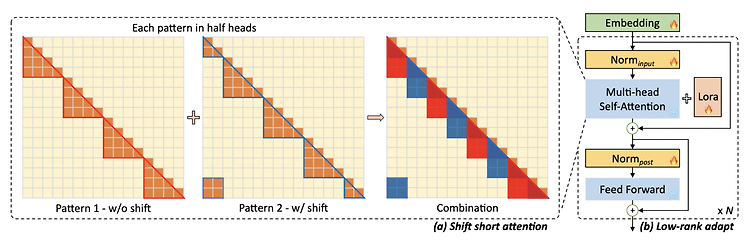
위에서 살펴본 shift short attention을 transformer의 multi-head self-attention 대신 사용하고,
여기에 Lora 기법을 더한 것이 LongLoRA 입니다.
기존 모델의 가중치를 그대로 사용(freeze)하는 부분은 얼음으로 표현되어 있고,
가중치 업데이트가 일어나는 부분은 불꽃으로 표현되어 있습니다.
여기서의 가장 핵심은 embedding과 normalization layer가 trainable하다는 것입니다.
LoRA만 사용한다고 하면 나머지 parameter를 전부 freeze하고 adapt하는 부분만 가중치를 업데이트하는데,
long context learning에 핵심 요소라고 볼 수 있는 embedding과 normalization을 건드렸다고 이해할 수 있습니다.
그렇다고 하더라도 이 둘은 연산되는 전체 파라미터 중에 아주 일부분만을 차지할 뿐입니다.
(LLaMA2 기준 embedding은 2% 미만, normalization은 0.004% 이하입니다)
Perplexity
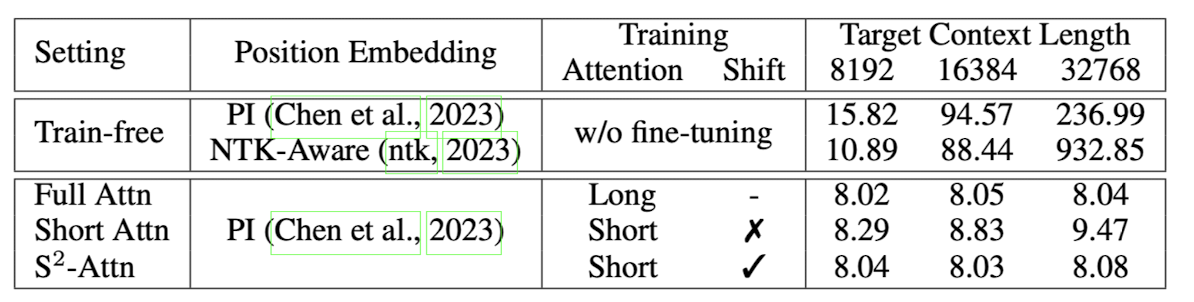
perplexity는 LLM의 생성 능력을 평가하는 지표로 많이 사용됩니다.
어떤 성능에 대한 태스크는 아니고, 각 step에서 토큰을 생성하기까지 고려되는 토큰의 평균 개수라고 볼 수 있습니다.
쉽게 말하자면 확신도라고도 할 수 있겠네요.
예를 들어 어떤 시점에서 토큰을 생성하는데 고려해야 하는 토큰의 개수가 20개인 것과, 10개인 것을 비교해본다면 후자의 경우가 훨씬 높은 '확신'을 갖고 토큰을 선택한 것이라고 해석할 수 있겠죠.
반대로 너무 많은 것을 고려해야 하는 전자의 경우 선택이 이뤄졌어도 찝찝한 상태에서 불확실하게 선택했다고 볼 수 있습니다.
이 수치는 context의 길이가 길어질수록 더욱 극단적으로 변하는데요, 당연한 것이 이전의 맥락을 고려하다보면 수만가지의 선택지가 생겨나기 때문입니다.
하지만 잘 학습된 모델일수록 전체 내용을 일관되게 해석함으로써 낮은 perplexity를 유지할 수 있게 되죠.
위 표의 값을 보면 Shift Short Attention을 적용한 경우, context length를 무려 32768까지 확장했음에도 불구하고 perplexity가 굉장히 낮은 값을 유지하고 있다는 것을 알 수 있습니다.
이를 Full Attention과 비교해본다면 perplexity는 비슷하지만 fine-tuning에 들어가는 비용이 압도적으로 적은 것이죠.
여러 실험 결과나 데이터셋 관련 내용은 포함하지 않았습니다.
궁금하신 분들은 논문을 참고해주세요!
개인적 감상
엄청 흥미로운 내용입니다.
사실 LoRA 이전과 이후로도 이런 식으로 attention 방식을 건드려서 효율적으로 계산하고자 하는 시도들은 많았던 것으로 알고 있는데, 이렇게 주목을 받는 데는 이유가 있겠죠?
논문 자체를 굉장히 직관적으로 잘 풀어서 작성했다는 생각도 듭니다.
코드로는 어떻게 구현되어 있는지 공부할 가치가 충분한 것 같습니다.
또한 이 방식의 가장 큰 장점은 기존의 technique들과 compatible하다는 것입니다.
논문을 보면 FlashAttention-2와 DeepSpeed stage 2/3를 적용하여 fine-tuning했다는 설명이 제시되어 있습니다.
또한 position encoding 관련해서 Position Interpolation을 사용했다고 하는데, 이것은 context 길이와 관련있는 내용으로 공부할 것들이 참 많다는 생각이 들었습니다.
출처 : https://arxiv.org/abs/2309.12307
LongLoRA: Efficient Fine-tuning of Long-Context Large Language Models
We present LongLoRA, an efficient fine-tuning approach that extends the context sizes of pre-trained large language models (LLMs), with limited computation cost. Typically, training LLMs with long context sizes is computationally expensive, requiring exten
arxiv.org
'Paper Review' 카테고리의 다른 글
최근(2023.09)에 나온 논문을 읽어보고 간단히 정리했습니다.
혹시 부족하거나 잘못된 내용이 있다면 댓글 부탁드립니다 🙇♂️
[MIT]
사전학습된 LLM의 context size를 확장하는 efficient fine-tuning 기법, LongLoRA.
sparse local attention 방식 중 하나로 shift shoft attention(S^2-Attn)를 제안하고,
trainable embedding & normalization을 통해 computational cost를 대폭 줄이면서도 기존 모델에 준하는 성능을 보임.
Fine-tugning을 위한 3K 이상의 long context question-answer pair dataset, LongQA 공개.
배경
LLM들은 이미 사전 정의된 context size를 갖고 있습니다.
하지만 이로 인해 LLM을 다양한 분야에 접목시키기 어렵다는 문제가 발생합니다.
예를 들어 2048개 토큰을 최대 context size로 지니는 LLaMA의 경우, 이를 초과하는 길이의 문서를 요약하는 등의 작업은 제대로 처리할 수 없게 되는 것이죠.
그래서 이 context window를 확장하고자 하는 다양한 시도들이 있었지만, transformer의 아키텍쳐는 context size의 quadratic하게 비례하는 연산량을 갖는다는 특징이 문제로 지적되었습니다.
엄청 단순하게만 생각해보면 context를 두 배로 확장하기 위해서는 네 배의 GPU 자원이 필요하게 되는 것입니다.
이런 한계를 극복하기 위해서 self-attention을 개선하여 연산량은 줄이되 기존 full attention만큼의 성능을 유지할 수 있도록 하는 시도도 끊임없이 이뤄지고 있습니다.
본 논문에서 제시하는 LongLoRA 역시 같은 맥락의 연구 결과입니다.
LongLoRA
shift short attention

본 논문에서는 shift short attention을 사용하고 있습니다.
이는 short attention 방식에 shift를 적용한 것으로 계산 과정은 위와 같이 시각화될 수 있습니다.
1) 우선 feature를 head 차원에 대해 반으로 쪼갭니다.
만약 8개의 head가 있었다면 이를 4개로 쪼개는 것입니다.
2) head chunk 중 하나가 그룹 사이즈의 절반만큼 이동합니다.
위 예시에서는 4개의 head가 2개로 쪼개지며 각 그룹은 2개의 head로 구성됩니다. 따라서 이것의 절반인 1(토큰)만큼 이동한 것으로 이해할 수 있습니다.
만약 head가 8개인 구조였다면 2(토큰)만큼 이동했을 것입니다.
3) 마지막으로 토큰들을 이번엔 배치 단위로 쪼개어 그룹을 형성합니다.
위 예시에서는 토큰이 8개인 상황을 다루고 있는데, 이때 각 그룹은 두 개의 토큰으로 구성됩니다. 즉 배치 사이즈가 2인 예시입니다.
이러한 방식으로 계산을 진행하는 shif short attention은 기존의 self-attention이 모든 토큰에 대해 계산하는 것과 달리, 각 배치 그룹마다 계산을 하게 되어 있고, shift를 통해 그룹 간 information이 전달(flow)되는 것으로 이해할 수 있습니다.
Architecture

위에서 살펴본 shift short attention을 transformer의 multi-head self-attention 대신 사용하고,
여기에 Lora 기법을 더한 것이 LongLoRA 입니다.
기존 모델의 가중치를 그대로 사용(freeze)하는 부분은 얼음으로 표현되어 있고,
가중치 업데이트가 일어나는 부분은 불꽃으로 표현되어 있습니다.
여기서의 가장 핵심은 embedding과 normalization layer가 trainable하다는 것입니다.
LoRA만 사용한다고 하면 나머지 parameter를 전부 freeze하고 adapt하는 부분만 가중치를 업데이트하는데,
long context learning에 핵심 요소라고 볼 수 있는 embedding과 normalization을 건드렸다고 이해할 수 있습니다.
그렇다고 하더라도 이 둘은 연산되는 전체 파라미터 중에 아주 일부분만을 차지할 뿐입니다.
(LLaMA2 기준 embedding은 2% 미만, normalization은 0.004% 이하입니다)
Perplexity

perplexity는 LLM의 생성 능력을 평가하는 지표로 많이 사용됩니다.
어떤 성능에 대한 태스크는 아니고, 각 step에서 토큰을 생성하기까지 고려되는 토큰의 평균 개수라고 볼 수 있습니다.
쉽게 말하자면 확신도라고도 할 수 있겠네요.
예를 들어 어떤 시점에서 토큰을 생성하는데 고려해야 하는 토큰의 개수가 20개인 것과, 10개인 것을 비교해본다면 후자의 경우가 훨씬 높은 '확신'을 갖고 토큰을 선택한 것이라고 해석할 수 있겠죠.
반대로 너무 많은 것을 고려해야 하는 전자의 경우 선택이 이뤄졌어도 찝찝한 상태에서 불확실하게 선택했다고 볼 수 있습니다.
이 수치는 context의 길이가 길어질수록 더욱 극단적으로 변하는데요, 당연한 것이 이전의 맥락을 고려하다보면 수만가지의 선택지가 생겨나기 때문입니다.
하지만 잘 학습된 모델일수록 전체 내용을 일관되게 해석함으로써 낮은 perplexity를 유지할 수 있게 되죠.
위 표의 값을 보면 Shift Short Attention을 적용한 경우, context length를 무려 32768까지 확장했음에도 불구하고 perplexity가 굉장히 낮은 값을 유지하고 있다는 것을 알 수 있습니다.
이를 Full Attention과 비교해본다면 perplexity는 비슷하지만 fine-tuning에 들어가는 비용이 압도적으로 적은 것이죠.
여러 실험 결과나 데이터셋 관련 내용은 포함하지 않았습니다.
궁금하신 분들은 논문을 참고해주세요!
개인적 감상
엄청 흥미로운 내용입니다.
사실 LoRA 이전과 이후로도 이런 식으로 attention 방식을 건드려서 효율적으로 계산하고자 하는 시도들은 많았던 것으로 알고 있는데, 이렇게 주목을 받는 데는 이유가 있겠죠?
논문 자체를 굉장히 직관적으로 잘 풀어서 작성했다는 생각도 듭니다.
코드로는 어떻게 구현되어 있는지 공부할 가치가 충분한 것 같습니다.
또한 이 방식의 가장 큰 장점은 기존의 technique들과 compatible하다는 것입니다.
논문을 보면 FlashAttention-2와 DeepSpeed stage 2/3를 적용하여 fine-tuning했다는 설명이 제시되어 있습니다.
또한 position encoding 관련해서 Position Interpolation을 사용했다고 하는데, 이것은 context 길이와 관련있는 내용으로 공부할 것들이 참 많다는 생각이 들었습니다.
출처 : https://arxiv.org/abs/2309.12307
LongLoRA: Efficient Fine-tuning of Long-Context Large Language Models
We present LongLoRA, an efficient fine-tuning approach that extends the context sizes of pre-trained large language models (LLMs), with limited computation cost. Typically, training LLMs with long context sizes is computationally expensive, requiring exten
arxiv.org