최근(2023.09)에 나온 논문을 읽어보고 간단히 정리했습니다.
혹시 부족하거나 잘못된 내용이 있다면 댓글 부탁드립니다 🙇♂️
[MIT, Meta AI]
initial token의 Key, Value를 attention 과정에서 keep하는 방식, Attention Sinks
유한한 길이의 attention window로 학습된 LLM이 무한한 길이의 sequence에 대해 일반화 할 수 있도록 하는 StreaingLLM.
배경
LLM이 여러 태스크에서 뛰어난 퍼포먼스를 보여주는 것은 맞지만, 입력이 특정 길이를 넘어서게 되면 이를 전혀 처리하지 못한다는 문제점을 갖고 있죠.
그런다고 입력 길이를 늘려주자니 attention 연산이 quadratic 하다 보니 무작정 늘리지도 못하는 것이 현실입니다.
본 논문에서는 attention 연산 방식을 개선하여 LLM이 학습에 사용했던 attention window 사이즈보다 큰 크기의 입력이 들어오더라도 이에 대한 일반화가 잘 이뤄질 수 있도록 하는 방식을 제안하고 있습니다.
initial 토큰이 태스크를 수행하는데 직접적인 영향을 주는 것은 아님에도 불구하고 많은 양의 attention score를 차지하고 있다는 실험 결과를 통해 attention sinks라는 개념을 도입했습니다.
Streaming LLM
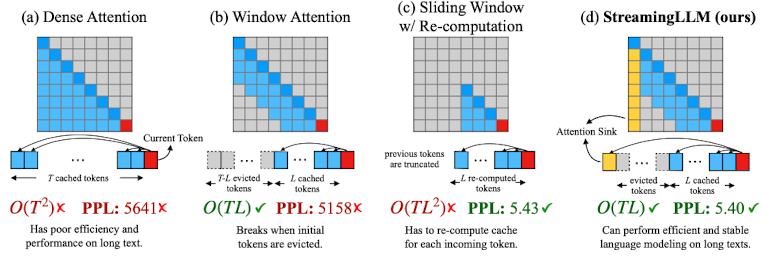
attention 비교
T는 전체 토큰의 개수를, L은 attention window의 크기를 나타냅니다. L은 이미지에서 보이는 것처럼 cached 토큰의 개수라고 볼 수 있습니다.
반면 evicted는 attention 연산에서 제외되었다는 것을 뜻하므로 그 길이는 T-L이 됩니다.
여기서의 언어 모델은 auto-regressive한 것들을 다루기 때문에 대각 성분의 우상단은 attention 연산 대상이 아닙니다.
(a) Dense Attention
O(T^2)의 시간 복잡도를 갖습니다.
즉 입력이 길어짐에 따라 연산량이 quadratic 하게 증가합니다.
뿐만 아니라 PPL(perplexity)도 지나치게 높아 정상적인 output을 만들어 낼 수 없다는 것을 알 수 있습니다.
(b) Window Attention
O(TL)의 시간 복잡도를 갖습니다.
전체 토큰의 개수 T에 대해 window size L 만큼의 cached token을 이용하여 attention 연산을 수행합니다.
따라서 시간 복잡도는 Dense Attention에 비해 압도적으로 낮다고 볼 수 있습니다.
그러나 PPL은 지나치게 높습니다.
(c) Sliding Window with Re-computation
O(TL^2)의 시간 복잡도를 갖습니다.
전체 토큰의 개수 T에 대해 window size L 만큼 attention 연산을 sliding 하며 반복 수행합니다.
위 이미지를 기준으로는 L re-computed tokens의 범위가 맨 왼쪽부터 오른쪽으로 sliding 했을 것이라는 뜻입니다.
PPL은 낮지만, 연산량이 결국 window 사이즈에 quadratic 하게 상승하기 때문에 활용 가능한 방식이 아닙니다.
(d) StreamingLLM (ours)
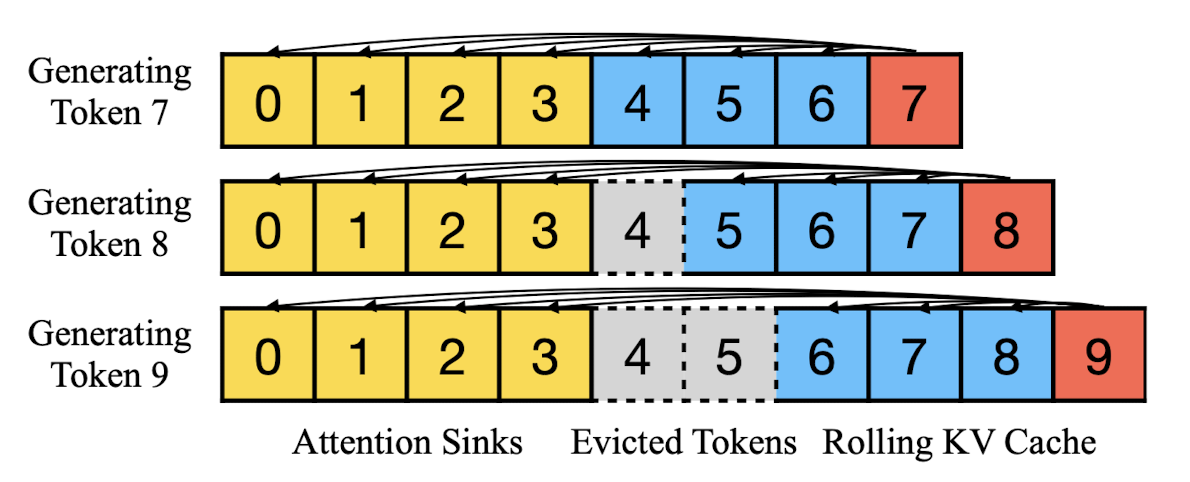
O(TL)의 시간 복잡도를 갖습니다.
몇몇의 초기 토큰을 attention sink로 삼고 window Attention을 적용합니다.
즉 '전체 토큰의 개수 T에 대해 window size L 만큼의 cached token'과 '초기 토큰'을 활용하여 attention을 수행합니다.
(논문에서는 이를 rolling cache라고 표현하고 있습니다. 이에 대해서는 RoPE 또는 ALiBi와 같은 최신 position encoding 기법을 모델에 따라 다르게 적용합니다)
따라서 Window Attention 자체에 비해서는 연산 시간이 조금 더 필요하겠지만 충분히 합리적인 연산량입니다.
게다가 PPL이 굉장히 낮습니다.
결국 시간 복잡도도 충분히 효율적이면서 long text를 처리하는데 어려움이 없는 attention 기법임을 알 수 있습니다.
attention 종류별 input 길이에 따른 PPL 측정 결과

위에서 설명한 것과 동일한 실험 결과가 나타나는 것을 알 수 있습니다.
빨간색으로 표현되는 StreamingLLM의 경우 시간 복잡도가 낮음에도 불구하고 Sliding Window with Re-computation에 준하는 PPL 수치를 보여줍니다.
이와 달리 Dense Attention은 input length가 사전 학습 당시의 window size를 초과하는 경우, 그리고 Window Attention은 input length가 cached되는 KV 사이즈(위에서 L이라고 지칭)을 초과하는 경우 그 성능이 급격하게 나빠지는 것(PPL이 급격하게 상승)을 볼 수 있습니다.
with / without Sink Token(s)
LLaMA-2 (2048 tokens) / Falcon, Pythia, MPT (1024 tokens) 모델 등에 대해 StreamingLLM이 적용 가능한 방식인지 확인합니다.

위 모델들에 대해 StreamingLLM을 적용하는 경우 input length가 4M까지 확장되어도 PPL이 정상적인 범주 내의 값을 갖는 것을 확인할 수 있습니다.
또한 모델의 사이즈별로 비교하는 경우, 모델의 크기과 PPL 값이 반비례하는 것으로 보아 scability한 특성을 지녔다는 것 또한 알 수 있습니다.
Pre-training LLMs with Attention Sinks
한편 이 방식이 사전 학습에서도 유의미한 성과를 낼 수 있는지 Pythia 모델 아키텍쳐를 기반으로 실험한 결과가 있습니다.
160M 개의 파라미터를 갖는 모델 두 개에 대해 attention sink를 포함하는 것과 그렇지 않도록 세팅하고 사전 학습을 진행합니다.
각 attention layer와 head에 대한 학습 결과를 시각화한 결과는 다음과 같습니다.

이를 보면 Sink Token을 활용하는 경우, 확실히 Sink Token에 대한 attnetion score가 초반 layer부터 굉장히 높게 나타나는 것을 알 수 있습니다.
심지어 10번 째 정도의 layer가 되면 다른 initial token에는 attention이 거의 되지 않는 것을 알 수 있습니다.
따라서 사전 학습 동안에 attention sink를 적용하는 것은 모델에게 주어지는 입력의 길이를 확장하는데 유의미한 영향을 줄 수 있는 것으로 해석 가능합니다.
SoftMax-off-by-One
한편 Softmax의 총합이 1이 되지 않도록 하는 SoftMax-off-by-One 이라는 방식이 있습니다.
이것은 사실 sink token을 전부 0으로 만드는 것과 동일한 효과를 지니게 됩니다.
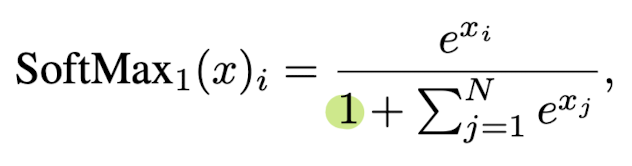

좌측은 해당 소프트맥스의 수식을, 우측은 해당 연산 방식을 택했을 때의 PPL 값을 나타냅니다.
따라서 기존에 제시되었던 방식을 개선했다는 점도 contribution이라고 볼 수 있을 것 같습니다.
개인적 감상
요즘에 반복적으로 접하게 되는 키워드가 positional encoding과 attention mechanism인 것 같습니다.
두 키워드 모두 길이가 더 긴 input을 모델에게 전달하고자 하는 연구들이 많다는 사실을 방증하는 것이겠죠.
개인적으로는 전자에 대한 이해도가 떨어지는 편이라서 공부를 더해야겠다는 생각이 들고, 후자의 경우엔 요즘 시각화도 굉장히 잘 되어 있고 설명도 충분해서 엄청 재밌는 접근들이라고 느낍니다.
다만 PPL에 대해 의구심이 생깁니다.
길이가 너무나도 긴 텍스트에 대해서 모델이 context를 제대로 이해하고 있는지를 이와 같은 방식으로 파악할 수 있는게 맞는가 싶은 생각이 듭니다.
물론 여러 개의 질문을 이어 붙이는 것도 방법이 될 수 있을 것 같긴 한데.. 뭔가 좀 더 정교한 평가 방식이 존재해야 이런 방식이 유의미한 성과를 낼 수 있다라고 받아들여질 것 같습니다.
출처 : https://arxiv.org/abs/2309.17453
Efficient Streaming Language Models with Attention Sinks
Deploying Large Language Models (LLMs) in streaming applications such as multi-round dialogue, where long interactions are expected, is urgently needed but poses two major challenges. Firstly, during the decoding stage, caching previous tokens' Key and Val
arxiv.org
