분류 전체보기

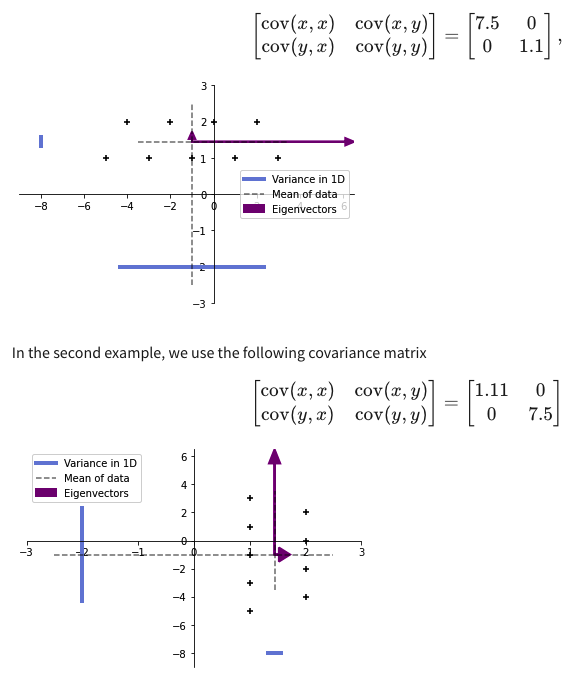
1. Effect on the mean 원래의 dataset에 2를 더하면 mean(평균)에 어떤 변화가 생길까? 아주 간단하게 평균값이 2만큼 더 커진 것을 확인할 수 있다. 원래의 dataset에 2를 곱하면 mean(평균)에 어떤 변화가 생길까? 원래의 평균의 2배가 되는 것을 알 수 있다. 이를 일반화한식이 마지막에 적혀있다. 2. Effect on the (co)variance variance는 데이터가 얼마나 흩어져있는지 모여있는지를 파악하는 지표이기 때문에 특정 값을 더한다고 하더라도 분산 자체는 변하지 않는다. 하지만 variance를 구하는 방식이 '데이터들이 평균으로부터 떨어진 거리의 제곱 합'이므로, 특정 값을 곱하게 되면 분산은 그 값의 제곱만큼 커지게 된다. 이를 2차원 이상(다차..

1. Variance of one-dimensional datasets D1 데이터셋에 포함되는 데이터들은 파란색 점으로, D2 데이터셋에 포함되는 데이터들은 빨간색 사각형으로 표현된다. 두 데이터셋은 같은 평균값을 가지지만 그 분포가 다르다는 것을 확인할 수 있다. 각 데이터셋의 평균값을 구하고 각 데이터들과의 편차를 구해본다. 계산해보면 D1에서 구한 것이 D2에서 구한 것보다 작다. 즉, D2의 분산이 더 큰 것이다. 분산은 데이터들이 얼마나 집중되어 있는지를 나타내는 지표로 쓰이게 된다. 구하는 식이 제곱의 합이므로 0이상의 값을 갖게 된다. 이 분산에 루트를 씌운 것을 standard variation(표준 편차)이라고 부른다. 2. Variance of 1D datasets 데이터셋의 평균,..

1. Mean of a dataset 데이터가 늘어날수록 흐려진다(blur) mean은 데이터를 대표하는 값으로 데이터셋에 포함되지 않는 값이 mean이 될 수 있다. 어떤 데이터셋의 모든 원소를 더하고 그 개수로 나누어주면 mean(평균)이 된다. 설명했던 것처럼 데이터셋에 포함되지 않는 값인 3.8이 이 데이터셋을 대표하는 값이 된다. 2. Mean of datasets 단순한 집합의 평균을 구하기(1문제) 벡터끼리의 평균을 구하기(3문제) 벡터에 scalar를 더하거나 곱한 뒤에는 평균이 어떻게 변할까? 표본 평균 구하기(1문제) n-1번째의 표본 평균에 특정 데이터가 추가되었을 경우 n번째의 표본 평균을 식으로 나타내기 평균(mean)의 정의를 전개하여 식을 조작해야 한다. 2차원을 1차원으로 ..

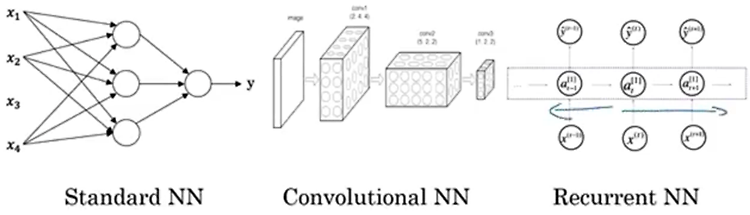
1. What is a Nerual Network? Housing Price Prediction size라는 input x를 받아 계산한 결과가 price라는 output y가 되고, 이것을 그래프로 표현한 것이다. input을 output으로 만들어주는 계산 과정이 포함된 부분을 도식화하면 동그라미가 되고, nueron이라고 한다. 위 그래프는 y의 값이 음수가 절대로 될 수 없기 때문에 y값이 전부 0으로 표현되는 수평한부분이 존재한다. 이런 형태의 그래프는 Rectified Linear Unit, ReLU 의 형태다. 지금 당장은 자세히 몰라고 되지만 향후 중요하게 다룰 내용이다. 지금은 single neuron만 존재하는 아주 간단한 형태의 neural network이고, 더 복잡한 NN을 만들기..

1. Product rule A(x)를 원래의 보라색 사각형을 제외한 나머지 세 부분을 합친 것으로 정의한다. 델타 x가 0으로 수렴하면 흰색 사각형의 면적은 0이 되므로 사라진다. 남은 초록색과 노란색 사각형의 면적에 대한 식으로 정리하고 양 변을 델타 x로 나눈다. 이는 미분의 정의에 맞게끔 식을 조정하는 과정이다. 마지막으로 식을 쪼갠 뒤 f(x)와 g(x)를 나누고 델타 x를 0으로 수렴하게 만들면 미분의 정의에 의해 마지막 식이 도출된다. 위 내용을 정리하면 Product Rule, 곱 규칙이 되고 식은 위와 같다. 곱의 미분 = 앞미분 + 뒷미분 2. Practicing the product rule product rule의 정의(2문제) '세 개를 연속으로 곱하는 경우는 어떻게 되는가' ; ..

1. Rise Over Run( rise: y축 증가량, run: x축 증가량) horizontal line(수평선)은 속도가 동일함을 의미한다. accleration: local gradient of a speed-time graph, function of time in graph deceleration: negative slope 시간에 따른 가속도 그래프는 위와 같다. 각 지점에서의 경사(slope)를 나타내고 있다. 노란색 그래프가 양수인 지점은 속도가 증가하고 있음을, 음수인 지점은 속도가 감소하고 있음을 나타낸다. 가속도 그래프를 한 번 더 미분한 그래프는 보라색으로 표현된다. 이것은 차의 흔들거림(jerk)를 나타내게 된다. 이런 과정을 거꾸로 하는 것이 anti-derivative라고 불리..